Chapter 9 方差

关于小样本的一点额外知识

考试不会考，了解即可

样本方差 $S^2$ 是总体方差 $\sigma^2$ 的无偏估计，但是标准差不无偏。

结论：正态分布的总体，样本的极差 $R$（range）的分布的均值是方差的某个倍数即 $d_2\sigma$，标准差也是方差的某个倍数即 $d_3\sigma$。于是，$R/d_2$ 就是 $\sigma$ 的无偏估计。样本很小的时候，用 $s$ 代替 $\sigma$ 不如用 $R/d_2$ 代替 $\sigma$。样本大的时候，用 $s$ 更好。

关于卡方分布的方差

方差的置信区间

根据第六章的知识点，$\frac{(n-1) S^2}{\sigma^2}$ 是服从卡方分布的。所以方差的置信区间应当是 $$\boxed{\frac{(n-1) S^2}{\chi_{\alpha / 2}^2}<\sigma^2<\frac{(n-1) S^2}{\chi_{1-\alpha / 2}^2}}$$。注意卡方分布的图像不是对称的！所以左右两边 $\frac{\alpha}{2}$ 的位置也不一样。所以在上述式子当中，用到了俩，式子左边是 $\chi_{\alpha / 2}^2$，右边是 $\chi_{1-\alpha / 2}^2$；标准差的区间就是开个根号。

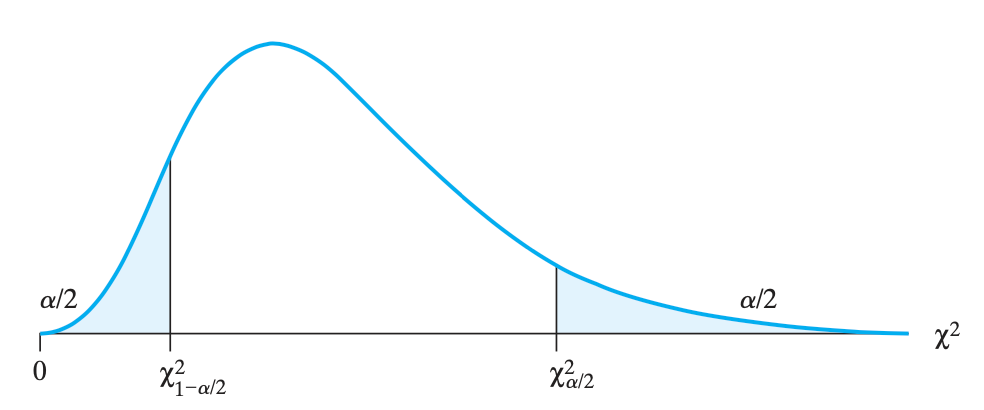
图的左边是 $\chi^2_{1-\alpha/2}$，右边是 $\chi^2_{\alpha/2}$，跟式子反过来了。反过来是因为推导区间的时候涉及到了减法和移项。

比较 $\sigma$ 跟某个值 $\sigma_0$ 的大小关系

因为不是对称的，所以这个表格不太好记忆。据说考试的时候是不要求记忆的，会给。

原假设是 $\sigma^2 = \sigma_0^2$，$\sigma_0$ 是题目给出来，让检验的，$\sigma$ 是真实的方差。真实的方差会影响到样本的 $S$。

这个表格其实跟前面的也基本一样，也是前两个单边的用 $\alpha$ 第三个双边用 $\alpha/2$，且其中 $$\boxed{\chi^2 = \frac{(n-1)S^2}{\sigma_0^2}}$$：

关于 F 分布的方差

比较两个总体方差的大小关系

这里要使用 F 分布的知识：$F = \frac{S_1^2}{S_2^2}$，回顾一下，F 分布实质上就是卡方分布除以各自的自由度。如果两个总体的方差相等，那么 F 分布的表达式就可以化简成这种简单的形式。如果方差不相等，那就是 $F=\frac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2}$。所以这里为了让式子简单一些，三行表格的原假设全都是 $\sigma_1^2 = \sigma_2^2$.

注意为了方便计算和查表，要让 $F > 1$，也就是分子用大的，分母用小的。这个表格其实跟前面的也基本一样，也是前两个是单边用 $\alpha$ 第三个是双边用 $\alpha/2$。

跟前面的不同点在于，第三行只有一个条件而不是两个。可以这样理解：因为 F 分布本身的表达式就已经涉及到俩了。

两个总体方差的比值的置信区间

两个总体方差不相等的时候，F 分布表达式稍微复杂：$F=\frac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2}$，$(1-\alpha)100\%$ 的置信区间是 $$\frac{\sigma_2^2}{\sigma_1^2} \in \boxed{\left(F_{1-\alpha / 2}\left(n_1-1, n_2-1\right) \frac{s_2^2}{s_1^2}, \quad F_{\alpha / 2}\left(n_1-1, n_2-1\right) \frac{s_2^2}{s_1^2}\right)}$$。