Chapter 4 概率分布
一些概念
随机变量 Random Variable:是一个函数,对每个输出指定一个数值。比如抛硬币,正面指定是 $1$,反面指定是 $0$。
概率分布 Probability Distribution:随机变量等于某一个数值 $x$ 的概率,就是概率分布。比如 $f(x) = P[X = x]$.对于离散变量的分布,可以画表格表示。概率分布一定满足 $f(x) \geq 0 \wedge \Sigma f(x) = 1$.
结合使用随机变量和概率分布,能把现实生活中的问题转换成数的问题。
定义大写 $F(x) = P[X \leq x] \forall x \in (-\infty, \infty)$. 这个叫做 累积分布 cumulative distribution,就跟前缀和似的。
因为 离散 的累积分布像是前缀和,所以 $P(a \leq X \leq b) = F(b) - F(a-1)$ 而不是 $F(b) - F(a)$!如果是连续的,那就无所谓了。
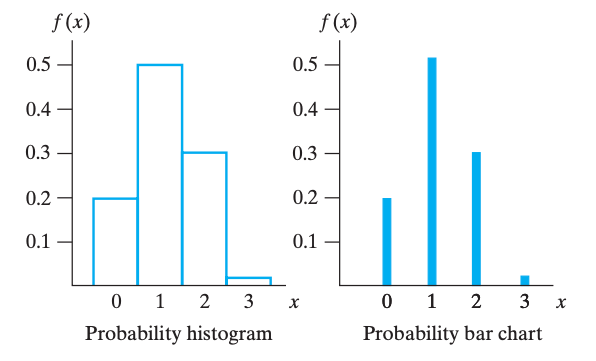
概率分布画图有两种,一种是 柱状图 histogram(左),另一种是 bar 图(右)。
二项分布 Binomial Distribution
注意,二项分布不是伯努利分布。伯努利分布就是二点分布($n=1$)。二项分布相当于二点分布重复 $n$ 次。
首先考虑 伯努利试验 Bernoulli trials,它满足以下条件:
- 每一个试验只有 两个输出。比如抛硬币
- 不管是第几次试验,两个输出的 概率都是恒定的,一个概率恒定是 $p$,另一个恒定是 $1-p$;也就是说每次试验概率保持一致。比如抛硬币
- 每一次试验之间是 独立 的,互不影响。比如抛硬币
在本节课中,额外加入一个条件:固定 $n$ 次。
定理:二项分布,进行 $n$ 次伯努利试验,每次成功概率是 $p$,那么恰好成功 $x$ 次的概率是 $$\boxed{b(x; n, p) = C_n^xp^xq^{n-x}}$$, 其中 $x=0,1,\cdots,n$,$q=1-p$。
定义大写 $$B(x; n, p) = \sum_{k=0}^xb(k; n, p)$$,其中 $x=0,1,\cdots,n$,$q=1-p$。相当于前缀和。
备注:假设检验:统计上,一般以 $5\%$ 作为界限。若根据某断言计算出概率小于 $5\%$,则一般认为断言是错误的,因为概率低的事件一般不会在偶然试验当中发生。
期望与方差
随机变量 $X$ 的平均值(期望值),记作 $\mu$ 或 $E(X)$,定义为:$$\mu=E(x)=\sum_x x \cdot f(x)$$;而随机变量 $X$ 的 方差(variance) 记作 $\sigma^2$,定义为:$$\begin{aligned}\sigma^2&=\sum_x(x-\mu)^2 f(x) \ &=E\left(X^2\right)-(E(X))^2\end{aligned}$$,等于「平方的期望减去期望的平方」;标准差(standard deviation) 记作 $\sigma$,定义为:$$\sigma=\sqrt{\sum_x(x-\mu)^2 f(x)}$$。
平方求和公式
$\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}$
常见分布的期望与方差
- 二项分布:期望 $np$,方差 $npq$
- 泊松分布:期望 $\lambda$,方差 $\lambda$
切比雪夫定理 Chebyshev’s theorem
也有的教材管它叫做「切比雪夫不等式」。
切比雪夫定理:对于一个随机变量,若期望是 $\mu$,标准差是 $\sigma$,那么取到一个在 $k$ 倍标准差以外的值的概率不会高于 $\frac{1}{k^2}$,即 $$\boxed{P(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2}}$$,也就是说,随机变量的所有值,基本都是接近于期望(平均)的。这个式子也叫做切比雪夫不等式。
泊松分布 Poisson
假如已知 $X$ 的平均值是 $\lambda$,$X = x$ 的概率是 $$\boxed{f(x;\lambda) = \frac{\lambda^xe^{-\lambda}}{x!}}$$。
在网上找到了一个泊松分布公式的记忆方法:
- 在马路上,有人戴着奇形怪状的帽子($\lambda^x$);你看到了,说:「咦($e$),有一个人($-\lambda$),」
- 「帽子很怪!($x!$)」
- 上面一句话是分子,下面一句话是分母,合起来就是泊松分布公式 $$\frac{\lambda^xe^{-\lambda}}{x!}$$
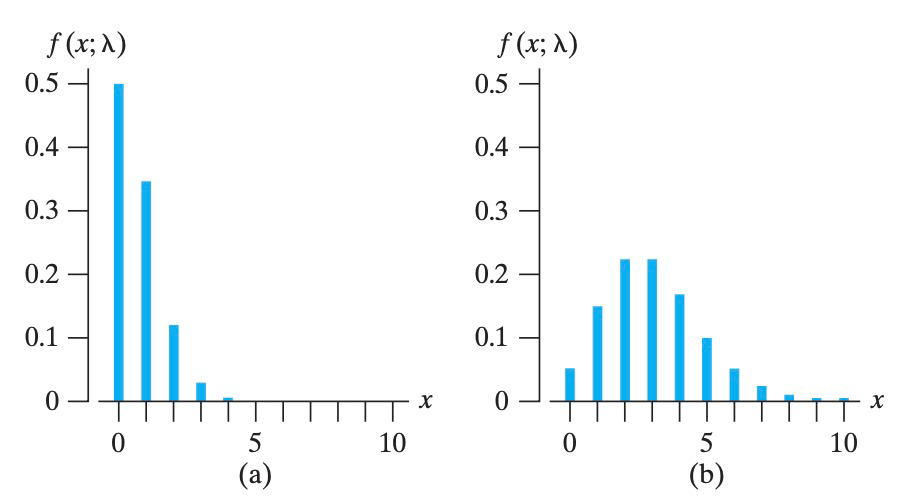
若 $\lambda$ 是整数,那么 $f_{\max}(x;\lambda) = f(\lambda-1;\lambda) = f(\lambda;\lambda)$;若 $\lambda$ 不是整数,则 $f_{\max}(x;\lambda) = f(\lfloor\lambda\rfloor;\lambda)$。下图分别表示 $\lambda=0$ 和 $\lambda=3$ 的情况:
用泊松分布近似计算二项分布
若 $n \to \infty$ 且 $p \to 0$,$np=\lambda$ 视作常数,那么二项分布的计算($n$ 太大组合数和幂次不好算)可以用泊松分布来近似:$$\boxed{b(x;n,p) = f(x;np)}$$,具体证明如下:$$\begin{aligned}b(x ; n, p) &= C_n^xp^xq^{n-x} \\ &= \frac{n !}{x !(n-x) !}\left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x} \\ &\approx \frac{\lambda^x e^{-\lambda}}{x !} \\ &= f(x; np)\end{aligned}$$;根据经验,$n\geq 20$ 且 $p \leq 0.05$ 的时候,或 $n\geq 100$ 且 $\lambda = np \leq 10$ 的时候,可以用这个近似。
泊松过程 Poisson Process
把一大段时间等分成若干份极短的时间 $T = n\Delta t$,假设每一段小时间上事件发生都是独立的,概率都是 $p = \alpha\Delta t$,且要么发生要么不发生(每个小区间上都是二项分布)。
若 $\Delta t$ 极小,就意味着 $n$ 非常大。
于是,$np = n\alpha\Delta t = \alpha T$,这意味着这个概率服从 $\lambda = np = \alpha T$ 的泊松分布,$\lambda$ 与 $T$ 成正比。i.e,如果 $T$ 是一天的时候 $\lambda=5$,那么 $T$ 取两天的时候,$\lambda$ 就是 $2\times 5=10$ 了。