Chapter 2 Part 4: 一大堆硬件电路(组合逻辑)
(共 70 页)
加法器
算术逻辑单元 ALU(Arithmetic and Logic Unit),是处理器的一个核心部分。可以完成整数加减乘除等操作。
加法器根据输入的个数,可以分为 半加器(half adder) 和 全加器(full adder) 两类。
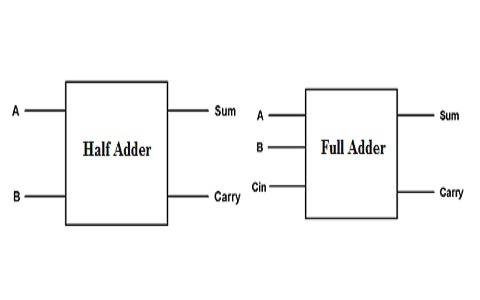
半加器
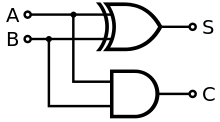
半加器通常是用于一位二进制数的加法运算,两个输入,两个输出,分别代表这一位的结果(Sum,S)以及进位(Carry,C)。半加器的结构示意图和真值表如下。
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
于是,$S = A \oplus B$,$C = AB$。
如果不用异或表示,那么结构图会复杂一点:
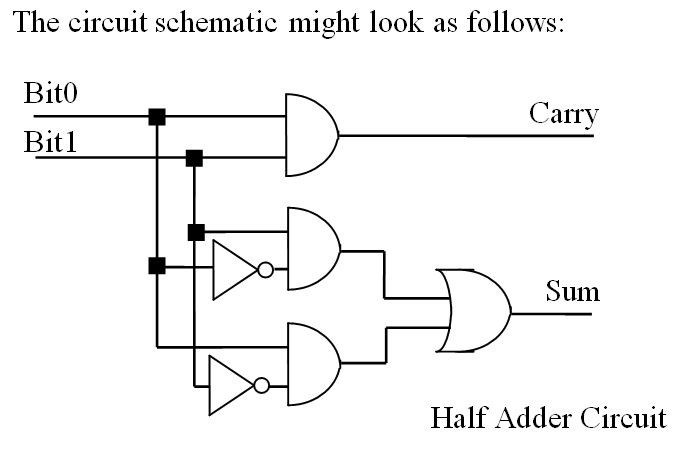
半加器的缺点是, 只能处理单独的一位数相加。假如是 11 + 01,应该等于 100,但是这时候半加器就算不出来了。
全加器
全加器相对于半加器,增加了一个输入 $C_{in}$ 表示低位的进位。这样,几个全加器级联在一起,就可以处理多位二进制数的加法。全加器的结构示意图和真值表如下所示。
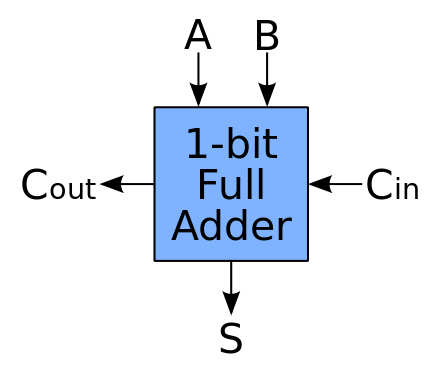
| A | B | C_in | C_out | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
事实上,全加器可以由两个半加器构成。第一个半加器处理两个加数,第二个半加器处理第一个的半加器的和以及低位的进位。第二个半加器的和则是全加器的和;两个半加器的进位的或,则是全加器的进位。
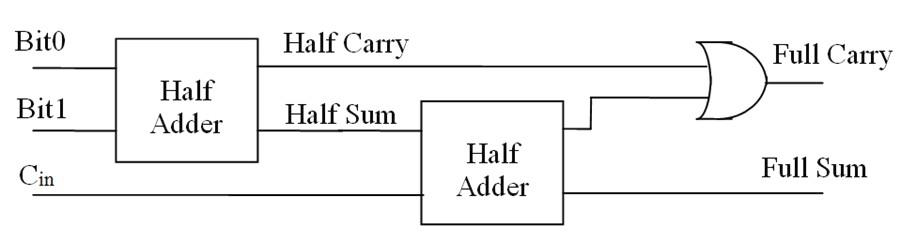
所以:
- $S = A \oplus B \oplus C_{in}$,就是三个输入全都异或起来
- $C_{out} = AB + (C_{in}(A \oplus B)) = AB + BC_{in} + AC_{in}$,换句话讲,$A, B, C_{in}$ 三个有俩是真,则 $C_{out}$ 真。
全加器的延迟
全加器的 关键路径(critical path,即经历最多逻辑门的路径) 经过两个异或门,终止于和位 $S$。假设异或运算需要三个单位的延迟(一级 invert、一级 and、最后一级 or),于是全加器的延迟就是六个单位。而进位模块比较快,只需要两个逻辑门,因此延迟是两个单位。
波纹进位加法器 Ripple Carry Adder
听起来很高级的样子。
实际上就是把多个全加器连起来,用来计算 N 位二进制加法而已。
其中,最低位不需要进位信号,所以最低位的全加器可以用半加器来代替。
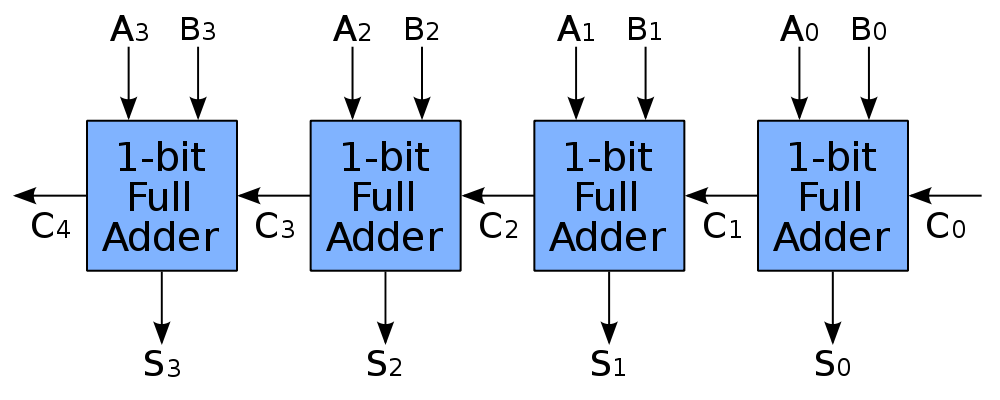
不过,虽然原理看起来很 low,但是结合补码表示法,可以构造出加法电路和减法电路。
加法电路和减法电路
课件里关于这种电路给出了三张图。依次是:原图、A+B 示意图、A-B 示意图。
实现 A-B 运算的基本原理就是把 B 直接用补码表示。整数转换成相反数,补码上体现为取反、加一。因此,在第三张图当中,若减法运算激活,则激活第零位的进位(相当于加一),然后把所有 B 的位都取反。
观察可以发现,每个 Full Adder 的下方,都有三个口;输入的 A 永远是最右边那个,而输入的 B 根据加法或者减法的要求,加法用中间那个,减法用最左边那个。
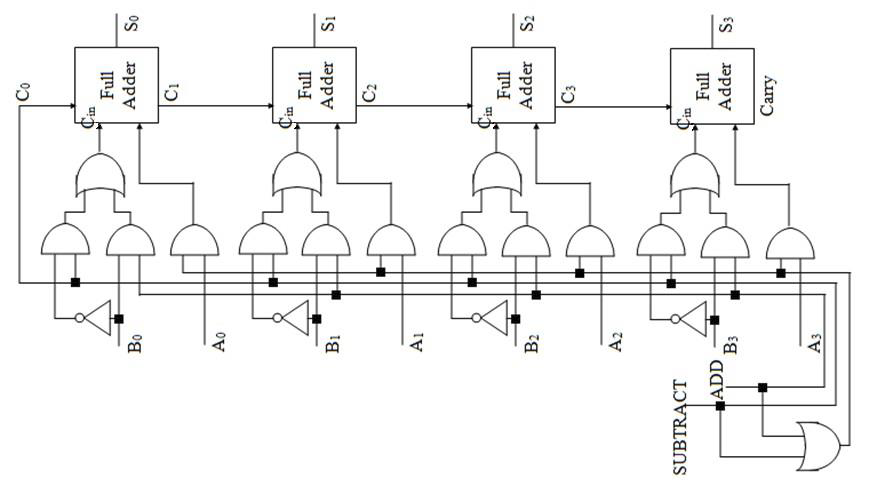

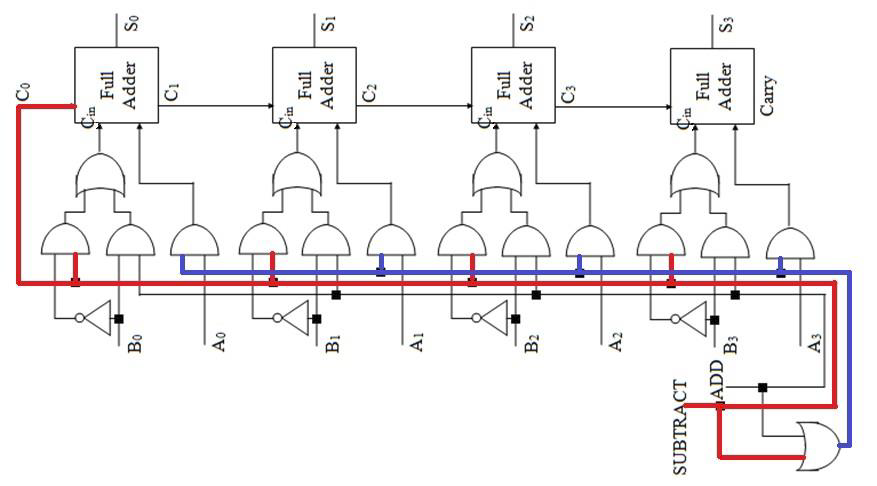
然而这种电路有一种非常大的缺陷——延迟非常高。因为每一个全加器都得等待上一个全加器算出来进位之后再继续算。当需要执行的加法位数很大,延迟就会高的难以忍受。
例如,对于一个 32 位整数的波纹进位加法器,延迟是来源是:
- 最高位从输入信号到进位输出的延迟,两个单位
- 其他 31 个全加器的延迟:每个全加器需要等待三个单位的延迟,共 93 个单位。
因此,32 位整数的波纹进位加法器,延迟总共是 95 个单位。
对于刚才计算的一点解释:
- 为什么每个全加器只需要等待三个单位而不是六个单位?因为每一位上的 A+B 都是一次性完成的,只有进位需要不停的等待,所以全加器的两个半加器,只有一个对延迟产生了主要贡献。
- 为什么是 31 个进位而不是 32 个?感觉可能是因为最高位即使有进位也会溢出,所以不需要考虑?反正课件上写的是 $32 \times 3=96$。
超前进位加法器 Carry Look Ahead Adder
原理
其实前面波纹进位加法器的延迟主要来源是,等待上一个全加器的进位。而所有全加器的直接相加的运算,是可以同时进行的:第 $i$ 位的和,是 $A \oplus B \oplus C$,这种异或运算可以一起快速完成。
因此,波纹进位加法器的优化思路,就是快速计算出所有位置上的进位。
事实上,所有位置上面的进位,还真的可以快速计算~
分析一下进位产生的原因,无非有两种,且不可能有产生两个进位的情况发生。
- $AB = 1$,产生一个进位
- $(A + B = 1) \wedge (C_{in} = 1)$,产生一个进位
于是,第 $i$ 位的进位 $C_{{out}_i} = A_i B_i + (A_i + B_i)(C_{{in}_i})$。
接下来不妨定义进位生成函数(Generate)$G_i = A_iB_i$,进位传送函数(Propagate)$P_i = (A_i + B_i)$。顾名思义,生成函数表示这一位是否会生成进位,而传送函数表示上一位的进位是否可以继续往后面传。这俩函数都可以在一个单位的延迟内计算得到。于是上式可以改写成: $C_{{out}_i} = G_i + P_i(C_{{in}_i})$ 。
$$\begin{aligned} C_{out,i}=& G_i + P_iC_{in,i} \\ =& G_i+P_i\left[G_{i-1}+P_{i-1}C_{in,i-1}\right] \\ =& G_i+P_i G_{i-1}+P_i P_{i-1}\left[G_{i-2}+P_{i-2}C_{in,i-2}\right] \\ & \vdots \\ =& G_i+P_i G_{i-1}+P_i P_{i-1} G_{i-2}+\cdots+ \left(\Pi_{j=1}^iP_j\right)G_0 + (\Pi_{j=0}^iP_j)C_{in,0} \\ =& \Sigma_{k=0}^i \left((\Pi_{j=k+1}^{i}P_j)G_k \right) + (\Pi_{j=0}^iP_j)C_{in,0} \end{aligned}$$
这个式子化到最后一步,分成左右两块。把 $\Sigma$ 符号当成一个巨大的 OR 门,$\Pi$ 符号当成一个巨大的 AND 门,最后左右俩再 OR 到一起。于是每个位置的进位,大概仅需三个单位的延迟就能计算得到。课件里面没有详细计算到底是多少延迟。
课件上给出了更简单的算式形式:
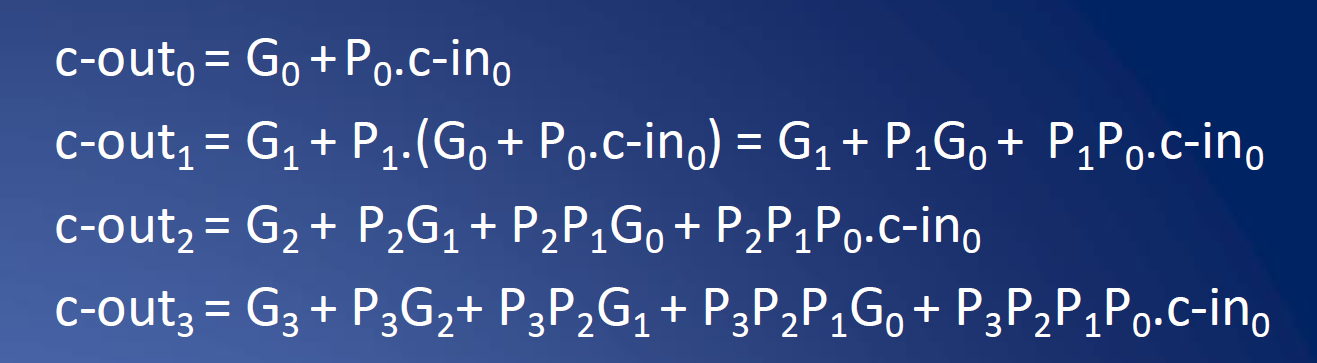
结构
于是,超前进位加法器(为了简单起见,以四位为例)分为三个部分
- 计算生成函数和传送函数:
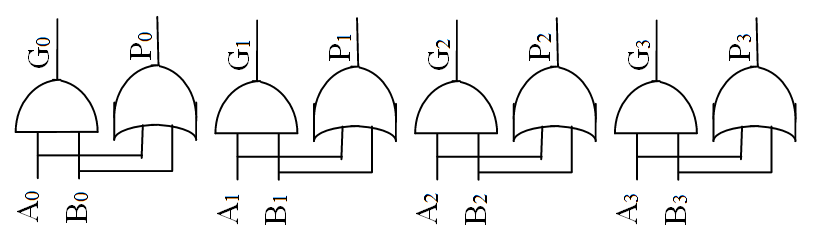
- 计算进位:
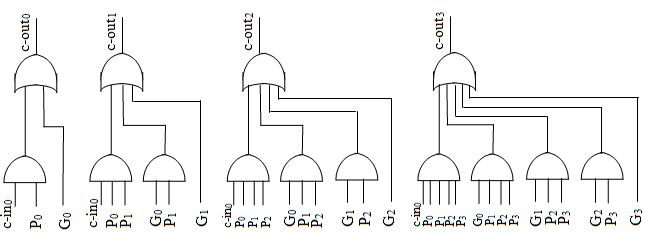
- 求和(应该是异或,这里图错了,画成普通的或了):
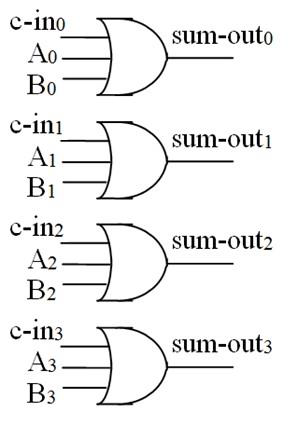
小结
这样做可以显著降低等待进位的时间,但是每一位上的计算,都有非常多的输入。如果是 $w$ 位的超前进位加法器,总共的输入数是 $w^2$ 级别(等差数列求和)。这意味着虽然节省了时间,但是电路的复杂程度急剧增加。
因此,如果位数非常的大,通常会把这个超前进位加法器拆开,比如如果要设计一个 64 位的高效加法器,可以用 4 个 16 位的超前进位加法器组合在一起来实现。
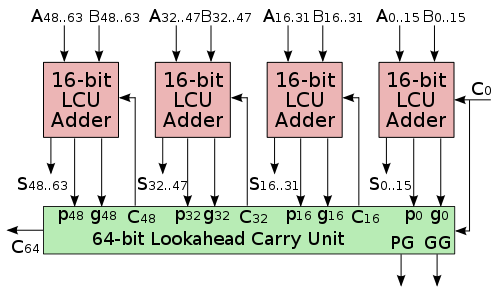
数据传输
有时候的数据传输会使用并行的形式以增加 吞吐量(throughout),就是一根地线连接很多信号线,比如电脑里一个主板上对应的 USB 针脚连了好几个 U 盘。
但是并行传输一般仅用于短距离传输,长距离场景不常见,原因是数据线 多重互联(multiple interconnections) 的成本限制。所以长距离传输的时候,通常把并行的转换到一根串行线上。
当 信令速度(signalling speed) 非常高的时候,由于 同步(synchronisation) 问题和 串扰(crosswalk) 问题,并行传输的效率也会受到很大影响,不如串行。现在的电脑几乎都是用 PCIe 串行总线(PCIe serial bus) 代替了之前的 PCI 共享并行扩展总线(PCI shared parallel extension bus)。
时分多路复用 (Time-division multiplexing)
当通过 通用串行总线(universal serial bus) 等 共享连接(shared connection) 连接设备的时候,通常会使用 时分多路复用 (Time-division multiplexing) 思想:这些设备与主机(host computer)共享信号线。总线由单个主机控制,而每个设备通过实现复杂的 USB 协议(protocol) 来读写数据。
多路复用器 Multiplexers,mux
数据选择器(Data Selector),或称 多路复用器(multiplexer,MUX),是一种可以从多个模拟或数字输入信号中选择一个信号进行输出的器件,使多个信号共享一个设备或资源。
换句话说,多路复用器是一种连接多个输入以及时共享单个输出的设备,这是一种实现时分复用的更简单的办法。输出的选择取决于控制输入的值。
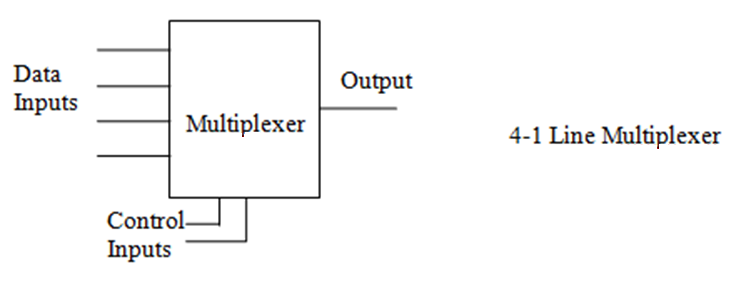
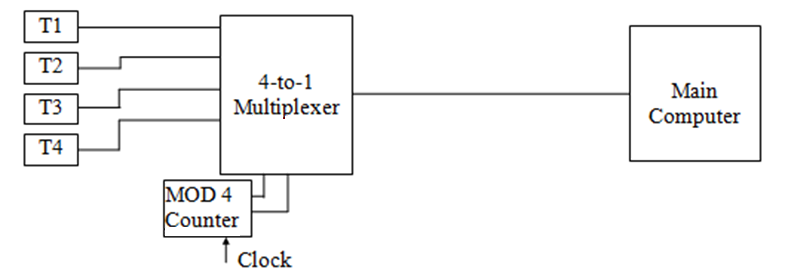
多路复用器的内部结构大概是这个样子,~~不过这好像不是重点内容,因为课件上连方程都没写~~
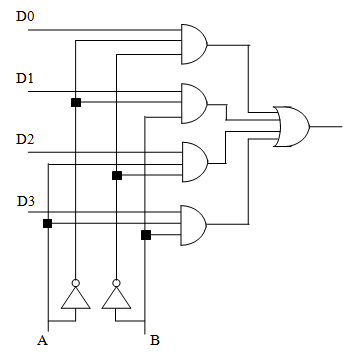
像这样,用时钟信号作为控制输入,就不需要什么乱七八糟的协议或者发生四个输入相互争抢输出了——轮流来。
多路分配器 demultiplexer,demux
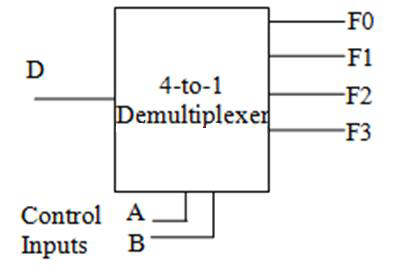
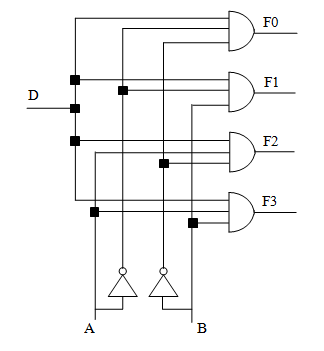
多路分配器 demultiplexer 顾名思义,作用与多路复用器相反:有一个输入、多个输出,根据控制输入的值来决定输出给多个输出当中的哪一个。比如有时候需要用一根数据线来实现多个不同设备的控制功能。
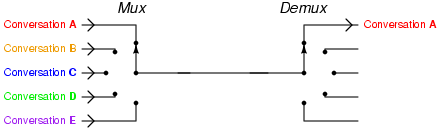
多路复用器与多路分配器结合使用,就可以将多个信号放到一根线里面传输,然后再在末端分离出来。
三态缓冲器(三态门,tri-state buffer)
缓冲器,是一种数字元器件,将输入原封不动的输出,不过可能会有一定的增强。当然,也有会将输入信号 invert 再输出的三态缓冲器。
三态缓冲器的输出,有 0、1、高阻态三种状态。高阻态(high impedance state),顾名思义,高电阻,等效于将输出的影响从后级电路中移除,就像强行断开了一样。这允许多个电路使用同一根输出线,如:总线 bus。
总线(bus) 是一组共享的通信线路和控制逻辑,用于互连计算机系统中的子系统组件。
一个三态逻辑缓冲器可以类比一个开关的工作情况。B 相当于控制开关。若 B 处于导通状态,则开关闭合,将输入 A 传送给输出 C;反之,若 B 断开,则相当于电路断开,电阻无穷大,前面没有与后面任何东西相连。
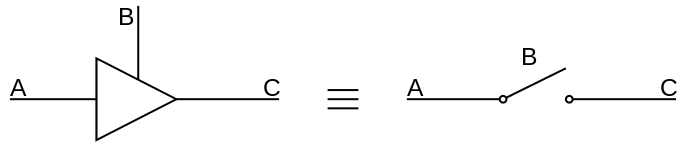
当多个电路同时想要使用总线(争吵,contention)的时候,三态缓冲器就要派上用场了:断开其中一个。否则两个电路可能会相互损坏,甚至是损坏总线。
解码器 Decoder
解码器可以把输入的信号转换成空间位置。如图,一共有两根输入信号,共 2^2=4 种输入值;解码器把这 4 个输入值一一对应到四个输出,并根据实际输入值选择激活一个对应的输出。更进一步,如果解码器有三个输入信号,那么就会对应八个输出。
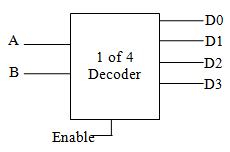
有的解码器(以及多路复用器)会额外带有一根激活线(enable line),并内置一个三态缓冲器。若没有激活,则利用三态缓冲器断开电路。电路结构示意图如下。
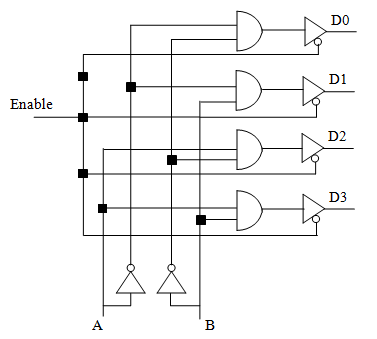
解码器的应用:选择和启用其他电路
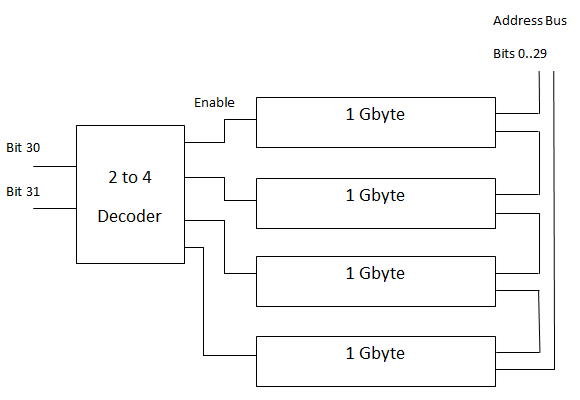
比如,输入的 $A$ 和 $B$ 可以用来表示内存地址,然后解码器输出去寻址、激活那个位置的东西。像 32 位的电脑,可以寻址 $2^{32}$ bits 也就是 $4$ 个 GB 的内存。可以先用一个 2-4 的解码器,根据内存地址的最高位、次高位,去确定这个地址到底对应了第几个 GB 的内存,然后激活那一块,剩下四分之三则不用管。
解码器的应用:switching function
思考解码器的特性,会发现,$2^n$ 个输出,与 $2^n$ 个最小项一一对应。
假设有一个布尔函数写成 SOP 形式之后是 $f = m_1 + m_3$,那么下面的这个电路,把解码器的输出 $m_1$ 和 $m_3$ 用一个 OR 门或起来,就相当于做了一次最小项求和(SOP),从而实现了函数值的输出。即:输入 $A$ 和 $B$,解码器和 OR 配合算出 $f(A, B)$ 然后输出。这就实现了一个 switching function。
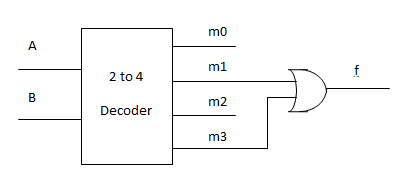
编码器 Encoder
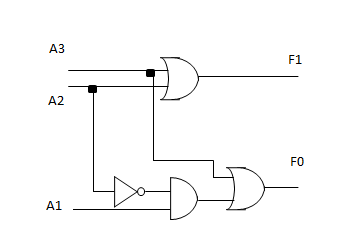
编码器就是解码器反过来呗。差不多就是:(假设)输入的一堆当中有一个是 1,就把这个输入的编号转换成二进制,再用输出表示。
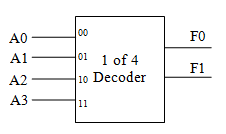
不过编码器的结构相比解码器而言,简单多了,甚至第零个输入可以直接不管他~
- $F_1 = A_2 + A_3$
- $F_0 = A_1 + A_3$
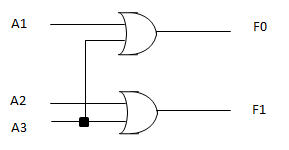
这种编码器可以应用于故障检测——把一堆东西连起来,如果一个出现了故障,就用编码器算出来到底是第几个发生故障。
然而,这一大堆输入,并不一定只有一个 1。咋整?答案是:设计优先级。如果有多个 1,我只关心优先级最高的一个 1。像这样,当 $A_3$ 是 1 的时候,剩下三个无论是啥我都不关心,用叉号表示。
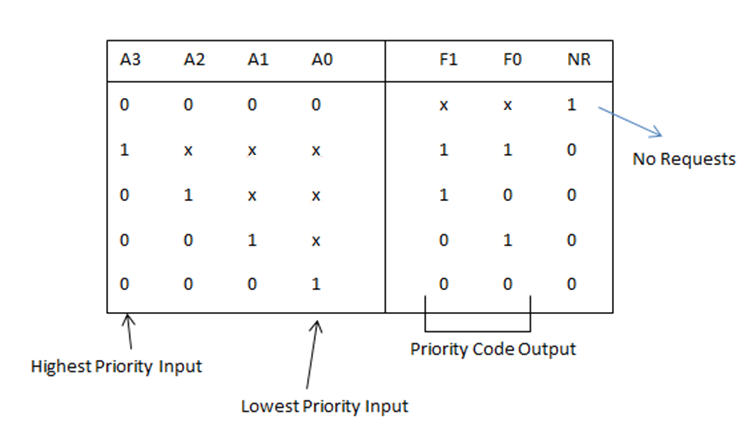
然而这时候,$F_0$ 的表达式有了一点变化,也新增了一个 $NR$ 的表达式:
- $F_1 = A_2 + A_3$
- $F_0 = A_1A_2' + A_3$
- $NR = A_0'A_1'A_2'A_3'$