Chapter 4 Part 2
(共 38 页)
由于一些原因,比如硬件故障(hard failure)或者软错误(soft errors),可能会导致数据在传输或存储的时候,出现一些错误。硬件故障,一般就是设备太老了,该淘汰了;软错误可能是有随机因素导致的。
数据存储的形式,是使用非常小的电荷,来表示 0 或者 1。可能突然一下子,老天爷打了个雷,然后某个地方的 0 就变成 1 了。
解决故障的方案,主要包括两种,一是:集成电路封装 chip packaging,二是:电缆屏蔽 cable shielding。这两种方案都具有低功耗、便携、快速传输、容量大等优点。
数据错误的检测与自动更正
对于软错误,可以附加一些额外的信息进行错误的检查。就像身份证号最后一位校验码一样。
首先定义一个概念:编码距离 distance of code。编码距离是指,从编码 S 变换到编码 T,需要改变多少位,也就是 S 和 T 有多少位不一样。
假如有一个 1bit 的数据,用 1bit 的信息来传输,那么这就不具有错误检查的能力。
而如果这 1bit 的数据(比如 A or B),用 2bit 的信息来传输(比如用 00 表示 A,11 表示 B),那么如果仅有一位出现异常,就检测到错误了。然而,这并不具备错误的自动更正能力。

为了实现错误的自动更正,可以使用 3bit 来传输这个信息。用 000 表示 A,111 表示 B。那么如果遇到了 001,那么大概率原始数据是 A,就自动更正到 A。如果数据是 110,就很可能想传输 B,自动更正到 B。

设 $C$ 表示可以被自动更正的位的数量,$D$ 表示可以被检查出有错的位的数量(根据定义,显然 $C \leq D$),那么有一个公式:$M - 1 = C + D$,其中 $M$ 是指最小的编辑距离。~~这个公式我也不知道怎么来的,反正课件就是这么写的~~。
网上说,要检查出 $d$ 位错误,需要 $d+1$ 的编辑距离。要修正 $d$ 位则需要 $2d+1$ 的编辑距离。毕竟修正的前提是检查,可以理解。
奇偶码 parity
对于单位错误检查,可以额外设置一个位,计算所有其他位的 $1$ 的个数是奇数还是偶数。也就是相当于计算异或啦。
In an even parity system, the parity bit is computed so that the number of 1’s in the data including the parity bit itself is even. In an odd parity system, the parity bit is computed so that the number of 1’s in the data including the parity bit itself is odd.
$P_{even}$ 用异或表示,$P_{odd}$ 用异或的非表示。
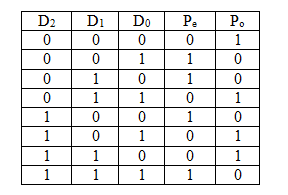
但这仅仅能用于检查错误,不能实现自动更正。
汉明码 Hamming (7, 4) Code
Hamming (7, 4) Code,顾名思义,就是把四位数加上三位扩展信息,变成七位数。
这是一个最小距离 3 代码,因此能够检测和纠正字中的任何一位错误或仅检测所有一位和两位错误。
构造方案
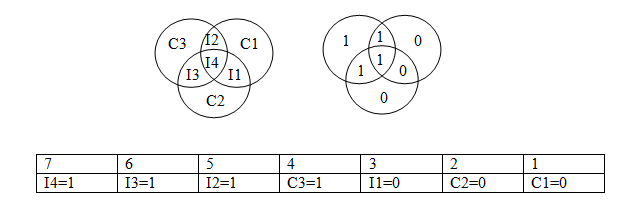
汉明码可以用韦恩图来构造。把原始的四位数据填进韦恩图的四个格子里面,然后对于三个大格子,填上包含的三个小格子的 $1$ 的个数 $\& 1$ 的值。
也就是说,汉明码分为 data bit 和 parity bit 两个部分。
如果有一个 data 位出现了错误,那么会同时影响相邻两个位置的奇偶性。如果 parity bit 出现了错误,那么只有一个圆圈会受到影响。
根据这个原理,就可以实现自动检测和自动更正了。如图,d 用阴影标注出来了错误数据的位置。

在实际应用中,对于一个汉明码,一共 $1 \sim 7$ 位数据,从左到右分别是 $7654321$。三个检查位的位置是 $1, 2, 4$,也就是 $2$ 的三个幂。
例如对于原始数据 $1110$,汉明码三个额外信息计算得到 $100$。那么编码到长度 $7$ 的地方去,就表示为:$\color{green}111\color{red}1\color{green}0\color{red}00$。其中绿色表示原信息,红色表示三个额外信息。
具体计算公式是假设原始数据是 $I_4I_3I_2I_1$,额外信息是 $C_3C_2C_1$:
- $C_1 = I_1 \oplus I_2 \oplus I_4$
- $C_2 = I_1 \oplus I_3 \oplus I_4$
- $C_3 = I_2 \oplus I_3 \oplus I_4$
扩展到 $N$ 位
如果不是四位数信息,而是 $N$ 位。要检查出错误来,需要多少额外的位呢?
答案是,设需要 $K$ 个额外位,需要保证:$2^K \geq N + K + 1$。
这个公式可以这样理解:其中 $N+K$ 表示有 $N+K$ 位有可能出错,而最后加一表示全都没错的情况。
错误检查
构造完了汉明码,还需要知道如何通过汉明码检查是否存在错误。
如果没有错误,需要满足一下几个式子:
- $C_1 \oplus I_1 \oplus I_2 \oplus I_4 = 0$
- $C_2 \oplus I_1 \oplus I_3 \oplus I_4 = 0$
- $C_3 \oplus I_2 \oplus I_3 \oplus I_4 = 0$
也就是把刚才 $C_1, C_2, C_3$ 的计算公式再套回去。
那如果出错了,会是什么样子的?
答案是,对于不同位出错,会有不一样的结果。具体表格如下
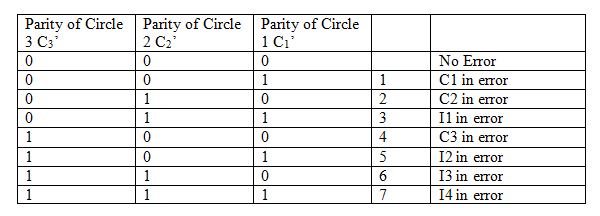
观察一下发现,如果是额外位出错了,那么只有自己会变成 $1$,其他俩该是 $0$ 还是 $0$。神奇吧?
更神奇的是,把 $C_3C_2C_1$ 当作二进制数,这个二进制数转换成十进制,就代表从右到左第几位出错。神奇吧?
两位出错
两位出错的话,由于汉明码是一种 distance-3 编码,会导致一些奇怪的问题。刚才上面那个表格是假设只有一位出错才有的情况。如果两位同时出错,按照之前的假设去分析,会得到错误的分析结果。
但是如果把汉明码扩展到 8 位(增加一位 parity bit)就可以解决(但并不是完全解决)双位错误的问题了。至于为啥不能完美解决,参考课件 36 页。
自动检测和修复位数据的电路示意图如下所示。
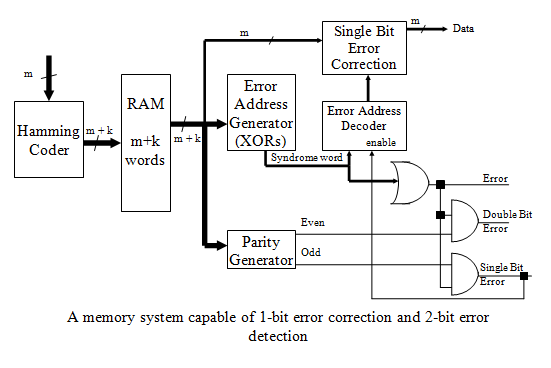
总结
(共 46 页)
-
DRAM 技术非常稳定
-
ECC Memory 通常用于服务器或非常重要的系统当中
-
ECC 降低内存访问性能(约 2%),不能把 ECC 芯片和非 ECC 混用在一起