Lecture 1. Foundations 基础知识
几个基本概念
数据结构
A data structure is a way to store and organise data in order to facilitate access and modifications.
算法
Informally, an algorithm is any well-defined computational procedure that takes some values, or set of values, as input and produces some values, or set of values, as output.
Algorithm: A tool for solving a well-specified computational problem.
算法的正确性 Correctness
正确的算法就是,无论对于什么输入,都会以正确的输出停止。那么,不正确的算法就是,对于一些输入,永不停止,或者以错误的输出停止。
然而,不正确的算法,也是有用处的。比如,Pollard Rho 验证大素数的算法,是不能保证 100% 正确的,但正确率足够在一些场景使用。
算法分析 Algorithm Analysis
大概就是,算算这个算法需要占用多少资源,比如耗时啦,内存啦,通信带宽啦。
通常不用时间来表示,而是说要运行多少步(steps)。毕竟跑的快的电脑和跑的慢的电脑可能差很多时间,然而运行多少步,对于所有电脑都一样的。
问:为啥不管常数?答:Constant numbers does not change the pattern of the rate of growth.
插入排序 Insertion Sort

插入排序就像是摸牌和理牌。
起初,手里没有牌,从牌堆摸牌,直接捏在手里。
之后从牌堆摸出来的牌,跟手里的牌从外往里依次比较大小。当遇到第一个小于等于摸到的牌,就插进去。
在示意图当中,橙色表示手里的牌,蓝色表示摸到的牌,白色表示牌堆剩下的牌。

伪代码如下:

循环不变式 Loop invariants
在上述伪代码当中,$i$ 表示的是当前摸到的牌的下标。在 while 循环开始之前,$A[1..i-1]$ 表示手里的牌,$A[i+1..n]$ 表示的是牌堆。
通过观察可以发现不管 $j$ 取值如何,$A[1..i-1]$ 都是排序过程开始之前的前 $i-1$ 个元素,它们的值的集合一直没变,只是被排的有序了。于是,$A[1..i-1]$ 的这个性质被称为 循环不变式 loop invariant。
循环不变式分为三个阶段:
- 初始化阶段:第一次循环开始之前,该性质成立。易证。
- 保持阶段:如果某次循环开始之前性质成立,那么下次循环开始之前性质依然成立。感性理解,每次插入新牌,原来的牌都要右移,对应着循环体迭代变量的自增。
- 终止阶段:循环终止后仍然成立。易证。
循环不变式有助于证明算法的正确性,尤其体现在终止阶段。
分析插入排序

注:图中的 $t_i$ 表示那个 while 循环对于 $i$ 取到特定值的时候的执行次数。
分析每一条语句的执行时间和执行次数。注意,普通的(不含 break 和 continue)for 和 while 循环的循环头的执行次数应该比循环体多一次,因为最后退出循环的时候还是要执行一次判断的。
那么算法的运行时间就是所有语句的运行时间乘以执行次数的和。根据上图,得到:$$\begin{aligned}T(n) &= c_1n + c_2(n-1) + c_4(n-1) + c_5\sum_{i=2}^n t_i+ c_6\sum_{i=2}^n(t_i-1) \\ &+ c_7\sum_{i=2}^n(t_i-1) + c_8(n-1)\end{aligned}$$.
最佳情况
当输入数组已经有序,就是插入排序的最佳情况($t_i=1$),此时 $$\begin{aligned}T(n) &= c_1n + c_2(n-1) + c_4(n-1) + c_5(n-1) + c_8(n-1) \\ &= (c_1+c_2+c_4+c_5+c_8)n - (c_2+c_4+c_5+c_8) \\ &= An + B\end{aligned}$$,故此时的插入排序关于 $n$ 是线性的。
最坏情况
但是如果输入数组完全是逆序的,那么每一个 $t_i$ 都被拉满了,导致最坏情况发生。此时 $t_i = i$,因为每一个新摸到的牌都要不停的比较一直到头。于是这时候,$\sum_{i=2}^n i = \frac{n(n+1)}{2}-1$,$\sum_{i=2}^n(i-1) = \frac{n(n-1)}{2}$,于是 $$\begin{aligned}T(n) &= c_1 n+c_2(n-1)+c_4(n-1)+c_5\left(\frac{n(n+1)}{2}-1\right) \\ & \space\space\space\space +c_6\left(\frac{n(n-1)}{2}\right)+c_7\left(\frac{n(n-1)}{2}\right)+c_8(n-1) \\ &= \left(\frac{c_5}{2}+\frac{c_6}{2}+\frac{c_7}{2}\right)n^2+\left(c_1+c_2+c_4+\frac{c_5}{2}-\frac{c_6}{2}-\frac{c_7}{2}+c_8\right) n \\ & \space\space\space\space-\left(c_2+c_4+c_5+c_8\right) \\ &= An^2 + Bn + C\end{aligned}$$,此时的插入排序的运行时间是关于 $n$ 的 二次函数 quadratic function。
平均情况
平均情况下,每一个新摸的牌,在已经摸到的牌当中,比它大的比它小的各占一半。因此 $t_i = \frac{i}{2}$。所以求和之后还是个二次函数。
渐进记号 Asymptotic Notation
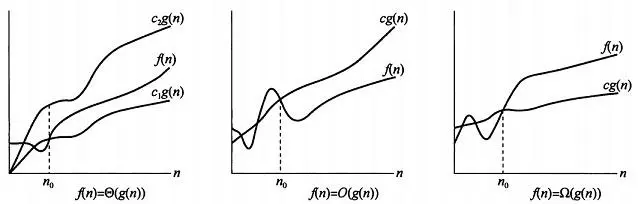

考试的时候要记得单词 asymptotic 的拼写!
一、$\Theta$ 记号

定义 $\Theta(g(n)) = f(n)$:存在 三个正常数 $c_1, c_2, n_0$,对于 $\forall n \geq n_0$,满足 $0 \leq c_1g(n) \leq f(n) \leq c_2g(n)$。
我们说 $g(n)$ 是 $f(n)$ 的 渐进紧确界(asymptotically tight bound)。
其实,$\Theta(g(n))$ 是一个集合, 所以实际上 $f(n) \in \Theta(g(n))$。然而通常我们用 $f(n) = \Theta(g(n))$ 来表达这个概念。其它几个记号同理。
杂谈
显然,当 $n$ 足够大的时候,低次项对于函数值的影响微乎其微。因此,所有的低次项,都可以忽略不计。另外,$c_1, c_2$ 值的选取可以参考最高次项的系数(coefficient) $k$:$c_1$ 略小于 $k$,$c_2$ 略大于 $k$。从而可知,最高次项的系数也可以忽略,因为这个系数只是影响了 $c_1, c_2$ 的取值。
关于证明复杂度的例子
证明:$\frac{1}{2}n^2 - 3n = \Theta(n^2)$
- 需要找出正常数 $c_1, c_2$ 和 $n_0$,对 $\forall n \geq n_0$,满足:$c_1 n^2 \leq \frac{1}{2} n^2-3 n \leq c_2 n^2$
- 上面不等式三个位置同时除以 $n^2$ 得到 $c_1 \leq \frac{1}{2}-\frac{3}{n} \leq c_2$
- 首先观察右半边不等式,由于都是正数,所以可以取 $c_2 = \frac{1}{2}$
- 为了让中间这一坨 $\frac{1}{2} - \frac{3}{n}$ 也是正的,要保证 $\frac{3}{n} < \frac{1}{2}$,可以取 $n=7$
- 然后 $c_1$ 就可以计算:$c_1 = \frac{1}{2} - \frac{3}{7} = \frac{1}{14}$
- 综上,$[c_1, c_2, n_0] = \left[\frac{1}{14}, \frac{1}{2}, 7\right]$ 可以满足刚才的式子,因此证明成立
二、大 $O$ 记号
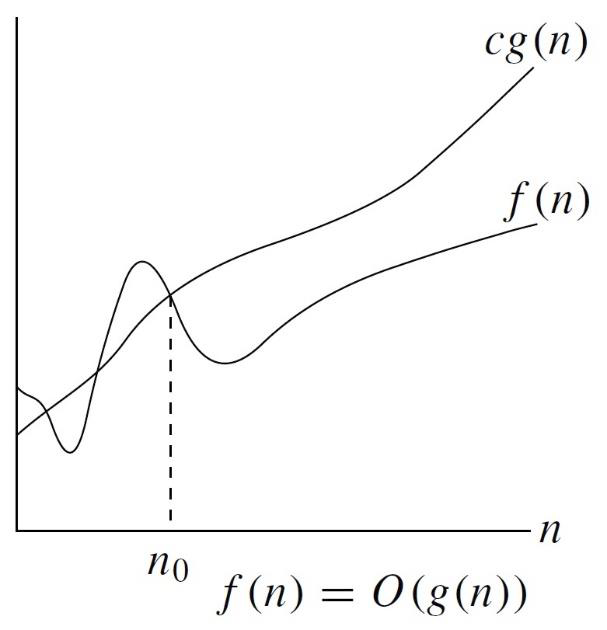
与 $\Theta$ 表示法不同。$\Theta$ 记号同时限制了上界和下界,而 $O$ 只是上界。
定义 $O(g(n)) = f(n)$:存在 两个正常数 $c, n_0$,对于 $\forall n \geq n_0$,满足 $0 \leq f(n) \leq cg(n)$。
大 $O$ 记号的用途之一是可以轻松的从代码结构看出时间复杂度的上限。比如正常的两层循环,那么时间复杂度就是 $O(n^2)$。从而,它常用于表示 最坏复杂度。
显而易见,$\Theta$ 比 $O$ 更加严格。因此,$[f(n) = \Theta(g(n))] \Rightarrow [f(n) = O(g(n))]$. 换句话说,$\Theta(g(n)) \subseteq O(g(n))$.
三、大 $\Omega$ 记号
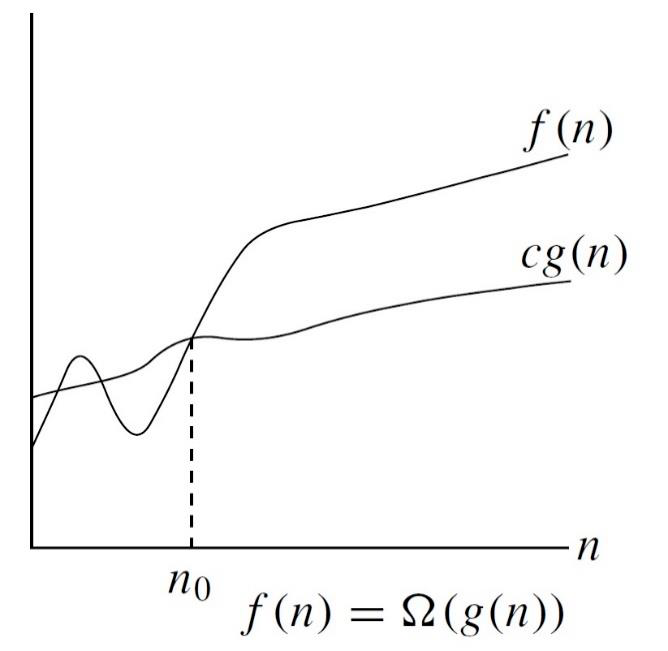
与 $O$ 相反。$O$ 限制的是上界,而 $\Omega$ 限制了下界。
定义 $\Omega(g(n)) = f(n)$: 存在 两个正常数 $c, n_0$,对于 $\forall n \geq n_0$,满足 $0 \leq cg(n) \leq f(n)$.
定理:对于任意两个函数 $f(n), g(n)$,$f(n) = \Theta(g(n))$ 当且仅当 $f(n) = O(g(n)) \wedge f(n) = \Omega(g(n))$.
$\Omega$ 记号的意义在于,指出了算法在 最优情况下的复杂度,比如插入排序的时间复杂度是 $\Omega(n)$,对已经有序的数组进行插入排序,复杂度是线性的。
四、小 $o$ 记号
大 $O$ 记号有一个缺点。就是说,$2n^2 = O(n^2)$,然而 $2n = O(n^2)$ 也成立。第二个等式显然不够 渐进紧确(asymptotically tight)。所以引入 小 $o$ 记号来表示 非渐进紧确 的上界。
定义 $o(g(n)) = f(n)$:对于任意 正常数 $c$,都存在 一个正常数 $n_0$,对于 $\forall n \geq n_0$,满足 $0 \leq f(n) < cg(n)$. 从式子的形式上来看,相比大 $O$ 记号,$c$ 从「存在」变成了「任意」,而且不等式右侧的 $\leq$ 变成了 $<$ 小于号。
这样一来,$2n = o(n^2)$ 成立,但是 $2n^2 \not= o(n^2)$。
用极限的形式来表达,就是 $$ \text{若 }f(n) = o(g(n))\text{,则 }\lim_{n \rightarrow \infty}\frac{f(n)}{g(n)} = 0$$
五、小 $\omega$ 记号
小 $\omega$ 和大 $\Omega$ 的关系也类似于小 $o$ 与大 $O$ 的关系——小 $\omega$ 记号表示 非渐进紧确 的下界。它有两种等价的定义,其一是:
定义 $\omega(g(n)) = f(n)$:对于任意 正常数 $c$,都存在 一个正常数 $n_0$,对于 $\forall n \geq n_0$,满足 $0 \leq cg(n) < f(n)$.
这样,$\frac{n^2}{2} = \omega(n)$,然而 $\frac{n}{2} \not= \omega(n)$.
用极限的形式来表达,就是 $$ \text{若 }f(n) = o(g(n))\text{,则 }\lim_{n \rightarrow \infty}\frac{f(n)}{g(n)} = \infty$$
记号小结
写证明题的时候需要分清楚 $f(n), g(n)$,以及 $c$ 乘给谁。
- 五个符号当中,无论是哪一个,$f(n)$ 是原始式子,写在外面!
- 五个符号当中,无论是哪一个,$g(n)$ 是写进记号括号里面的!
- 五个符号当中,无论是哪一个,$c$ 都是乘给 $g(n)$ 的!
最重要的:$\Theta, O, \Omega$ 的 $c$ 是存在即可,而 $o, \omega$ 的 $c$ 是 任意值!换句话说,$o$ 与 $O$、$\omega$ 与 $\Omega$ 定义式虽然长得一样,但 $o, \omega$ 要求对于任意的 $c$ 都成立,比 $O, \Omega$ 要求存在一个 $c$ 更加严格。
记号性质
传递性 Transitivity
五个记号都具有传递性。
$$ \begin{aligned} & f(n)=\Theta(g(n)) \text { 且 } g(n)=\Theta(h(n)) & \Rightarrow f(n)=\Theta(h(n)) \\ & f(n)=O(g(n)) \text { 且 } g(n)=O(h(n)) & \Rightarrow f(n)=O(h(n)) \\ & f(n)=\Omega(g(n)) \text { 且 } g(n)=\Omega(h(n)) & \Rightarrow f(n)=\Omega(h(n)) \\ & f(n)=o(g(n)) \text { 且 } g(n)=o(h(n)) & \Rightarrow f(n)=o(h(n)) \\ & f(n)=\omega(g(n)) \text { 且 } g(n)=\omega(h(n)) & \Rightarrow f(n)=\omega(h(n)) \end{aligned} $$
对称性 Symmetry
对于大 $\Theta$ 记号,满足 $$f(n) = \Theta(g(n)) \text{ 当且仅当 } g(n) = \Theta(f(n))$$
转置对称性 Transpose Symmetry
对于大 $O$ 与大 $\Omega$ 之间、小 $o$ 与小 $\omega$ 之间,满足:
$$ \begin{aligned} & f(n)=O(g(n)) \text { 当且仅当 } g(n)=\Omega(f(n)) \\ & f(n)=o(g(n)) \text { 当且仅当 } g(n)=\omega(f(n)) \end{aligned} $$
代数关系形式
可以把这些记号之间的关系想象成代数中的数值关系,如:
- $f(n) = O(g(n))$ 类似 $a \leq b$
- $f(n) = \Omega(g(n))$ 类似 $a \geq b$
- $f(n) = \Theta(g(n))$ 类似 $a = b$
- $f(n) = o(g(n))$ 类似 $a < b$
- $f(n) = \omega(g(n))$ 类似 $a > b$