Chapter 5 概率密度 Probability Density
这一章的重点内容是正态分布与联合分布
连续随机变量和概率密度函数
对于区间 $[a,b]$,分成 $m$ 个区间,每个区间长度都是 $\Delta x$,第 $i$ 个区间的高度记作 $f(x_i)$,一段小区间的概率就是这段的面积。这个 $f(x_i)$ 就是概率密度函数。
如果 $\Delta x$ 足够小,那么 $f(x_i)$ 就是一个光滑的函数图。整个的面积 $\sum_{i=1}^m f(x_i)\Delta x_i$。
所以,$$\begin{aligned}P(a\leq X \leq b) &= \sum_{i=1}^m f(x_i)\Delta x_i \\ &= \int_a^bf(x)\text{d}x\end{aligned}$$。
由于是连续的,所以对于一个 单独的点上的概率,是零,因为线的面积是零。于是:$$P(a\leq X \leq b) = P(a < X < b)$$。
这个叫做 概率密度函数(probability density function),也可以叫 做概率密度,满足:
- $\forall x$, $f(x) \geq 0$
- $\int_{-\infty}^{\infty}f(x)\text{d}x = 1$
它的累积分布函数 $F(x)$,显然满足:
- 定义式:$$F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\text{d}t$$
- 一段上的概率:$$P(a \leq x \leq b) = \int_a^b f(x)\text{d}x = F(b) - F(a)$$
- 导数:$$\frac{\text{d}F(x)}{\text{d}x} = f(x)$$,因为「先积分再求导就是函数本身」
例子 5.2(课本 5.3),为啥 $k=8$
期望和方差
定义期望 $$\mu = E(x) = \int_{-\infty}^{\infty}xf(x)\text{d}x$$,定义方差 $$\begin{aligned}\sigma^2 &= \int_{-\infty}^{\infty}(x-\mu)^2f(x)\text{d}x \\ &= \int_{-\infty}^{\infty}x^2f(x)\text{d}x - \mu^2 \\ &= E(x^2) - (E(x)^2) \end{aligned}$$,依然满足「平方的期望减去期望的平方」。
回顾:分部积分
$$\begin{aligned}\int u(x)v'(x)\text{d}x &= u(x)v(x) - \int v(x)\text{d}u(x) \\ &= u(x)v(x) - \int v(x)u'(x)\text{d}x \end{aligned}$$,可以简写成 $$\begin{aligned}\int u \text{d}v = uv - \int v\text{d}u\end{aligned}$$
LIATE
按照以下优先级顺序,从上往下依次选择 $u = u(x)$,从下往上选择 $\text{d}v = v'(x)\text{d}x$:
- 对数函数,$\ln x$ 等
- 反三角函数,$\arctan(x)$ 等
- 幂函数(代数函数),$x^2$, $3x^{50}$ 等
- 三角函数,$\sin(x)$ 等
- 指数函数,$e^x$ 等
正态分布 normal distribution(在 $\mathbb{R}$ 上取值)
定义正态分布表达式:$$f(x;\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$,其中的 $\mu$ 和 $\sigma^2$ 分别表示期望和方差,但是这里的计算(积分)不做要求。
根据图像可以得知,正态分布图像是以 $\mu$ 为对称轴,左右对称的。

标准正态分布(在 $\mathbb{R}$ 上取值)
期望是零、方差是一 的正态分布叫做 标准正态分布(standard normal distribution):$$f(x; 0, 1) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$,它的积分也不做要求。
(标准正态分布习惯上喜欢用字母 $z$ 代替 $x$),它的概率密度函数(Excel 可以算)是: $$\begin{aligned} & F(z) = P(Z \leq z) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^z e^{\frac{-t^2}{2}} \text{d}t \ & F(-z) = 1 - F(z)\end{aligned}$$。
关于分位点 $z_{\alpha}$
$P(Z > z_\alpha) = \text{val}$ 的点就是 $z_\alpha$,即 $F(1 - Z_\alpha) = \text{val}$,在 Excel 当中可以用 NORM.S.INV() 计算。
换句话说,$z_\alpha = \text{val}$ 表示,横坐标 $\text{val}$ 之后的部分的面积是 $\alpha$.
$z_{0.01}=2.33$,$z_{0.05}=1.96$,$z_{0.025}=1.645$,这三个分位点在数据分析和假设检验等领域很常用。
正态分布转化到标准正态分布
对于一个普通正态分布函数,先平移 $\mu$ 个单位,期望就从 $\mu$ 变成 $0$ 了;再伸缩到 $\frac{1}{\sigma}$,标准差就从 $\sigma$ 变成 $1$ 了,于是它变成了一个标准正态分布函数。
因此,如果 $X$ 满足正态分布,那么 $Z = \frac{X - \mu}{\sigma}$ 就满足标准正态分布。
于是,对于正态分布:
$$\begin{aligned} & P(a\leq X \leq b) \\ =& P\left(\frac{a-\mu}{\sigma} \leq \frac{X-\mu}{\sigma} \leq \frac{b-\mu}{\sigma} \right) \\ =& P\left(\frac{a-\mu}{\sigma} \leq Z \leq \frac{b-\mu}{\sigma} \right) \\ =& F\left(\frac{b-\mu}{\sigma}\right) - F\left(\frac{a-\mu}{\sigma}\right)\end{aligned}$$,也就是说所有正态分布都可以转化成标准的正态分布再进行计算。
用实数正态分布逼近整数正态分布
$X$ 在图中用 $[X - 0.5, X + 0.5]$ 表示。因此:
- $P_1(X < 8) = P(X \leq 7.5)$
- $P_1(X \leq 8) = P(X \leq 8.5)$
- $P_1(X = 8) = P(7.5 \leq X \leq 8.5)$
- $P_1(X \geq 8) = P(X \geq 7.5)$
- $P_1(X > 8) = P(X \geq 8.5)$
用正态分布近似计算二项分布
棣莫弗-拉普拉斯中心极限定理 de Moivre-Laplace Central Limit Theorem
之前已经用泊松分布进行过近似计算。
若随机变量 $X$ 服从参数是 $n$ 和 $p$ 的二项分布,且 $n$ 很大,那么组合数和阶乘很难算。此时的 动图图像(使用 WolframAlpha 模拟得到) 跟正态分布长得很像。


于是只要 $n$ 足够大,那么 $$Z = \frac{X - np}{\sqrt{npq}}$$ 将会满足标准正态分布。按照规律经验,当 $np$ 与 $nq$ 均 $\geq 15$,则可以用标准正态分布进行估算二项分布。
由于二项分布当中的 $X$ 都是整数,所以这里要注意 $.5$ 的问题。
对数正态分布 log-normal distribution(在 $(0,\infty)$ 上取值)
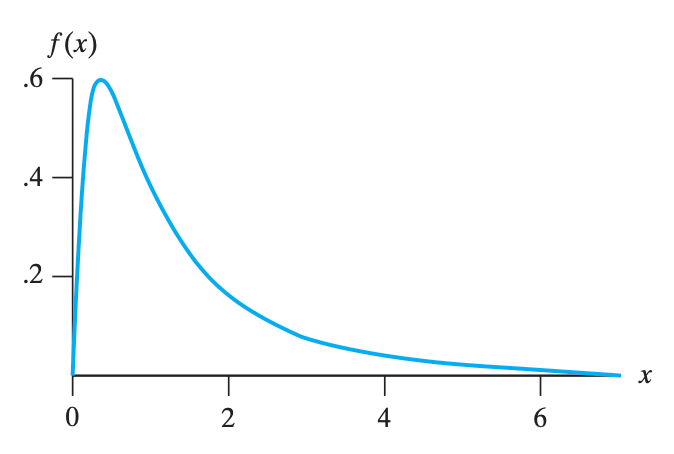
$$f(x)= \begin{cases}\frac{1}{\sqrt{2 \pi} \beta} x^{-1} e^{-\frac{(\ln x-\alpha)^2}{2 \beta^2}}, & \text { for } x>0, \beta>0 \\ 0, & \text { elsewhere }\end{cases}$$,其中 $\alpha$ 是 $\ln x$ 的均值,$\beta$ 是 $\ln x$ 的标准差。这个式子里面多了个奇怪的 $x^{-1}$,这其实是 $\ln x$ 的导数。根据某个定理,变换的时候必须要乘上这个导数。
助教课:若某一个变量 $X$,经过对数变换 $Y = \ln X$ 之后,假如 $Y$ 服从正态分布即 $Y=\ln X \sim N(\alpha,\beta^2)$,那么就说 $X$ 服从对数正态分布。
若 $X$ 服从对数正态分布,那么 $\ln X$ 就服从正态分布,从而 $\ln X$ 可以经过变换变成服从标准正态分布。因此对数正态分布的计算也可以转化成标准正态分布的计算
$$\int_a^b \frac{1}{\sqrt{2 \pi} \beta} x^{-1} e^{-\frac{(\ln x-\alpha)^2}{2 \beta^2}} \text{d} x=F\left(\frac{\ln b-\alpha}{\beta}\right)-F\left(\frac{\ln a-\alpha}{\beta}\right)$$
$\ln x$ 的期望和标准差分别是 $\alpha$, $\beta$,对于 $x$ 是:
- 期望:$e^{\alpha + \frac{\beta^2}{2}}$
- 方差:$e^{2\alpha + \beta^2}(e^{\beta^2}-1)$
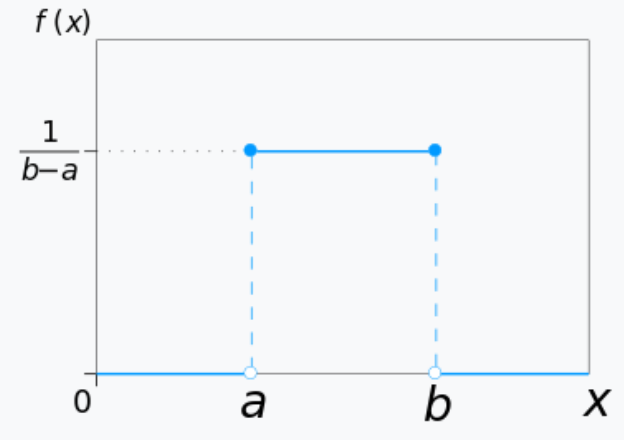
均匀分布 uniform distribution(在 $\mathbb{R}$ 上取值)
均匀分布有两个参数 $\alpha$,$\beta$,它的概率密度函数是 $$f(x) = \begin{cases}\frac{1}{\beta - \alpha} &, \alpha < x < \beta \\ 0 &,\text{otherwise}\end{cases}$$。均值是 $\frac{\alpha + \beta}{2}$,方差是 $\frac{(\beta - \alpha)^2}{12}$。
伽马分布 Gamma Distribution(在 $(0,\infty)$ 上取值)
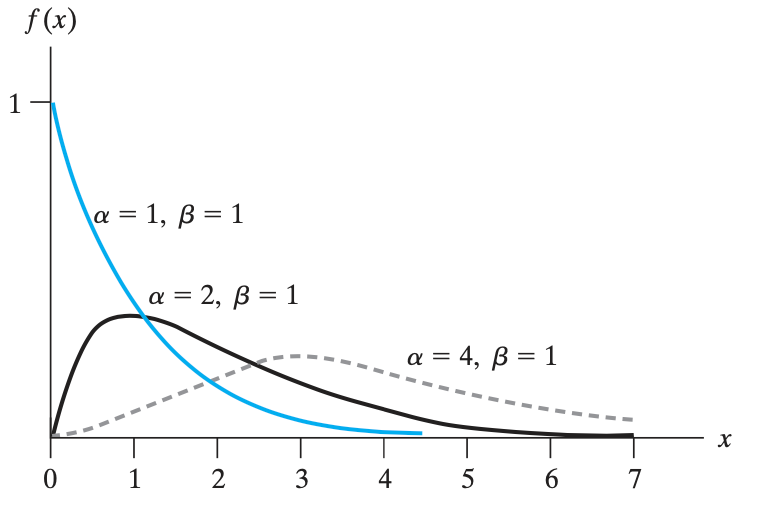
定义伽马分布(取值只能是正的):$$f(x)= \begin{cases}\frac{1}{\beta^\alpha \Gamma(\alpha)} x^{\alpha-1} e^{\frac{-x}{\beta}}, & \text { for } x>0, \alpha>0, \beta>0 \\ 0, & \text { elsewhere }\end{cases}$$,其中 $\Gamma(\alpha)$ 是伽马函数的值,定义为:$$\Gamma(\alpha) = \int_0^{\infty}x^{\alpha-1}e^{-x}\text{d}x$$。
伽马函数性质
当 $\alpha > 1$,有 $$\Gamma(\alpha) = (\alpha - 1)\Gamma(\alpha-1)$$,这个性质可以用 $\Gamma(\alpha+1)$ 推导。
另外,由于 $$\begin{aligned}\Gamma(1) &= \int_0^{\infty}e^{-x}\text{d}x \\ &=-e^{-x} \mid_0^{\infty} \\ &= -(0 - 1) \\ &= 1 \end{aligned}$$,因此当 $\alpha$ 是正整数的时候,伽马函数表示阶乘,容易得到:$$\Gamma(\alpha) = (\alpha-1)!$$。顺带一提,$\Gamma(0.5) = \pi$。
伽马分布的期望与方差
- 期望:$\alpha\beta$
- 方差:$\alpha\beta^2$
指数分布
当 $\alpha=1$,伽马分布就变成了一个 指数分布(exponential distribution) 的形式:$$\boxed{f(x)= \begin{cases}\frac{1}{\beta} e^{\frac{-x}{\beta}}, & \text { for } x>0, \beta>0 \\ 0, & \text { elsewhere }\end{cases}}$$。
二级结论:关于泊松过程与指数分布
先回顾一下,泊松分布的式子是:$f(x;\lambda) = \frac{\lambda^xe^{-\lambda}}{x!}$,泊松过程是 $\lambda=\alpha T$ 即 $f(x;\lambda)=\frac{(\alpha T)^xe^{-\alpha T}}{x!}$。
若在一个泊松过程当中,单位时间内的发生次数是 $\alpha$,那么,相邻两次发生之间的 间隔时间,服从参数 $\beta = \frac{1}{\alpha}$ 的指数分布。代入指数分布的式子,得到 $$\boxed{f(x) = \alpha e^{-\alpha x}}$$。
例题 5.13
假如每个小时平均会有三辆卡车到仓库卸货。求:
- 连续两辆车到达之间的间隔时间,少于 5min 的概率
- 连续两辆车到达之间的间隔时间,不少于 45min 的概率
方法一:用泊松过程计算
- 此时 $\lambda = 3 \times \frac{5}{60} = 0.25$。题目要求间隔时间小于 5min,那 5min 内再来 1 个、2 个、3 个…只要不是零个,都行。所以答案就是 1 减去 0 个来的概率 $$1 - f(0;\lambda) = 1-0.779 = 0.221$$
- 此时 $\lambda = 3 \times \frac{45}{60} = 2.25$。题目要求间隔时间至少 45min,那 45min 内一个都不能来,只能是零个,所以答案是 $$f(0;\lambda) = 0.105$$
方法二:用指数分布计算
- $$\int_0^\frac{1}{12}3e^{-3x}\text{d}x = 1-e^{-\frac{1}{4}} = 0.221$$
- $$\int_\frac{3}{4}^\infty3e^{-3x}=e^{-\frac{9}{4}} = 0.105$$
贝塔分布 Beta Distribution(在 $(0,1)$ 上取值)
定义贝塔分布 $$f(x)= \begin{cases}\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}, & \text { for } 1>x>0, \alpha>0, \beta>0 \\ 0, & \text { elsewhere }\end{cases}$$,期望方差分别是 $$\mu=\frac{\alpha}{\alpha+\beta}, \quad \sigma^2=\frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$$。
韦伯分布 Weibull distribution(在 $(0,\infty)$ 上取值)
$$f(x)= \begin{cases}\alpha \beta x^{\beta-1} e^{-\alpha x^\beta}, & \text { for } x>0, \alpha>0, \beta>0 \\ 0, & \text { elsewhere }\end{cases}$$,它的累积分布函数是 $$ F(x)=1-e^{-\alpha x^\beta}, \quad x>0 $$,它的期望和方差分别是 $$\begin{aligned} & \mu = \alpha^{-\frac{1}{\beta}}\Gamma\left(1+\frac{1}{\beta}\right) \\ & \sigma^2 = \alpha^{-\frac{2}{\beta}}\left\{\Gamma\left(1+\frac{2}{\beta}\right)-\left(\Gamma\left(1+\frac{1}{\beta}\right)\right)^2\right\} \end{aligned}$$,表示寿命或生存时间的时候,有可能用到韦伯分布,具体例子参考课件 example 5.15。
联合分布 joint distribution
关于两个变量联合起来。
先考虑 离散 的随机变量 $X_1, X_2$,那么 $P(X_1 = x_1 \wedge X_2=x_2)$ 的值,服从联合分布。
边际分布 marginal probability distribution
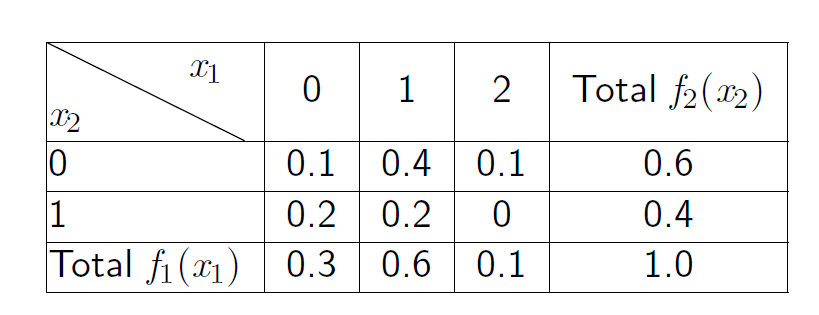
对于 离散 的变量,就是表格求和。形式化的说:$$P\left(X_1=x_1\right)=f_1\left(x_1\right)=\sum_\mathbf{x_2} f\left(x_1, x_2\right)$$,也就是固定 $x_1$,遍历 $x_2$ 求和。
如果变量是 连续 的,那就把求和换成积分:$$\boxed{P\left(X_1=x_1\right)=f_1\left(x_1\right)=\int_{-\infty}^{\infty} f\left(x_1, x_2\right)\text{d}\mathbf{x_2}}$$。注意求和的是 $x_1$ 还是 $x_2$。
概率密度函数
定义 $f(x_1,x_2)$ 表示单点的概率密度函数,那么一个区间上的密度函数呢?
$a_1 \leq X_1 \leq b_1$, $a_2 \leq X_2 \leq b_2$,那么这个范围上的密度函数是:$$\int_{a_2}^{b_2} \int_{a_1}^{b_1} f\left(x_1, x_2\right) \text{d}x_1\text{d}x_2$$。大写的累积分布函数,就是无穷到 $(x_1,x_2)$ 范围上的密度函数: $$F(x_1,x_2)=\int_{-\infty}^{x_2}\int_{-\infty}^{x_1}f(u,v)\text{d}u\text{d}v$$。
二重积分的计算
二重积分的常用方法是,降维到一重积分。关键是考虑二重积分的区域(底面)。底面假如是矩形区域,那就比较简单,如果不是矩形,那就复杂一点。
假如,底面是,直角边贴着或垂直于 $x$ 轴、斜边是 $y=x$ 的直角边长度为 $1$ 的等腰直角三角形:$$\int\int_Df(x,y)\text{d}x\text{d}y=\int_0^1\left(\int_0^xf(x,y)\text{d}y\right)\text{d}x$$。其中,$x\in[0,1]$,$y\in[0,x]$,积分符号的上标下标就是对应变量的范围。这样是先积了 $y$ 再积 $x$,也可以反过来:$$\int\int_Df(x,y)\text{d}x\text{d}y=\int_0^1\left(\int_y^1f(x,y)\text{d}x\right)\text{d}y$$。
对于底面是圆 $x^2+y^2=1$ 的情况,$$\int\int_Df(x,y)\text{d}x\text{d}y=\int_{-1}^1\left(\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}f(x,y)\text{d}y\right)\text{d}x$$。其中,$x\in[-1,1]$,$y\in[-\sqrt{1-x^2},\sqrt{1-x^2}]$,积分符号的上标和下标还是对应变量的范围。由于极佳的对称性,反过来也一样:$$\int\int_Df(x,y)\text{d}x\text{d}y=\int_{-1}^1\left(\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}f(x,y)\text{d}x\right)\text{d}y$$。
注意,计算关于 $y$ 的积分的时候,要把 $x$ 当作常量。计算关于 $x$ 的积分的时候,$y$ 当作常量。
老师说考试的题目也就是个矩形的难度。
条件概率(判断独立)
对于 离散 的,若 $f_1(x_1 \mid x_2) = f_1(x_1)$,那么就意味着这个条件概率跟 $x_2$ 无关,即 $f(x_1,x_2) = f_1(x_1)f_2(x_2)$,于是,两个随机变量是独立的。注意,以上两个式子,都需要满足对于所有的 $x_1,x_2$,才能得到结论。
对于 连续 的,$F(x_1,x_2) = F(x_1) \cdot F(x_2)$ 则独立。但是这个式子也能化简成 $f(x_1,x_2) = f_1(x_1) \cdot f_2(x_2)$,也就是联合概率密度等于两个对应的边缘密度。
总结起来说,无论是离散的还是连续的,判断独立,公式可以用一样的:$$f(x_1,x_2) = f_1(x_1) \cdot f_2(x_2)$$。
条件概率密度 conditional probability density
定义:$$f_1(x_1 \mid x_2) = \frac{f(x_1, x_2)}{f_2(x_2)}$$ 表示 $x_2$ 条件下 $x_1$ 的概率,其中边缘概率 $f_2(x_2) \neq 0$
期望
对于离散的,$E(X) = \sum_{x_i}x_if(x_i)$,对于连续的,就换成积分 $\int_\infty^\infty x_if(x_i)$。
扩展一下。如果现在考虑一个离散的 $x$ 的函数 $g(x)$,那么 $$E(g(x)) = \sum_{x_i}g(x_i)f(x_i)$$,注意求和好里面是 $g$ 函数,而概率密度那里不是 $f(g)$ 而是 $f$。如果连续就类比换积分。
二元函数的期望
对于离散:$$E(g(x_1,x_2)) = \sum_{x_1}\sum_{x_2}g(x_1,x_2)f(x_1,x_2)$$,连续换积分形式。
期望的线性性与方差的性质
- $E(aX + b) = aE(X) + b$
- $\operatorname{Var}(aX + b) = a^2\operatorname{Var}(X)$
对于 $i\in[1,k]$,当 $X_1, X_2, \cdots, X_k$,则根据期望的线性性,任意时刻有 $$E(a_1X_1+a_2X_2+\cdots a_kX_k) = a_1E(X_1)+\cdots+a_kE(X_k)$$。当它们 独立 的时候,还有 $$\boxed{\operatorname{Var}(a_1X_1+a_2X_2+\cdots+a_kX_k) = a_1^2\operatorname{Var}(X_1)+\cdots+a_k^2\operatorname{Var}(X_k)}$$,这个式子的意义在于,独立的时候,期望增加到 $n$ 倍,方差没有变成 $n^2$ 倍而是 $n$ 倍,也就是标准差只变成了 $\sqrt n$ 倍,也就是降低了风险。所以买股票的时候,五万块钱分成五份买五个不同行业的,相比五万块钱全都投给同一个,风险更低。
还有一个意义:为什么要多次测量取平均值?每次测量都是独立的,服从相同的分布(例题 5.29),那么测量 $n$ 次,期望不变,方差会变成 $\frac{\sigma^2}{n}$。
当 $X_1, X_2$ 独立,那么:
- $X_1-X_2$ 的期望是 $E(X_1)-E(X_2)$,方差是 $\operatorname{Var}(X_1)+\operatorname{Var}(X_2)$
- $X_1+X_2$ 的期望是 $E(X_1)+E(X_2)$,方差是 $\operatorname{Var}(X_1)+\operatorname{Var}(X_2)$
也就是说:
- $E(X_1 \pm X_2) = E(X_1) \pm E(X_2)$
- $\operatorname{Var}(X_1 \pm X_2) = \operatorname{Var}(X_1) + \operatorname{Var}(X_2)$,不管前面是啥,后面一律是加
推论
对于独立同分布的随机变量(简单样本),若总体的平均值是 $\mu$,方差是 $\sigma^2$,那么 对于这个样本 来说:
- 平均值 $E(\overline X) = \mu$
- 方差 $Var(\overline X) = \frac{\sigma^2}{n}$
协方差 covariance
定义:协方差(也可记为 $\operatorname{Cov}(X_1,X_2)$) $$ \operatorname{covariance}(X_1,X_2) = E\left[\left(X_1-\mu_1\right)\left(X_2-\mu_2\right)\right]$$。当 $X_1$ 与 $X_2$ 是独立的的时候,它们的协方差就是 $0$。(但如果协方差是 $0$,不一定独立,比如:$y=\sqrt{1-x^2}$ 的协方差是 $0$,这个有点复杂,暂不关注)。
方差可以是平方的期望减去期望的平方,协方差也可以是「乘积的期望减去期望的乘积」:$$\operatorname{Cov}(X_1,X_2) = E(X_1X_2) - \mu_1\mu_2$$。
协方差越大,线性相关性越小。