Lecture 3. Hash Tables 哈希表

哈希表是实现 字典操作（dictionaries）的高效的数据结构。

哈希表在最坏情况下，退化成普通的链表，查找的时间复杂度是 $\Theta(n)$；然而只要规划合理，查找操作可以达到 $O(1)$ 的平均时间复杂度。

像 Python 语言内置的字典（dictionary），就是用哈希表实现的。然而 Python 的字典是有序的，我觉得这可能会让时间复杂度退化到 $\log$ 级别。

直接寻址表 Directed-address table

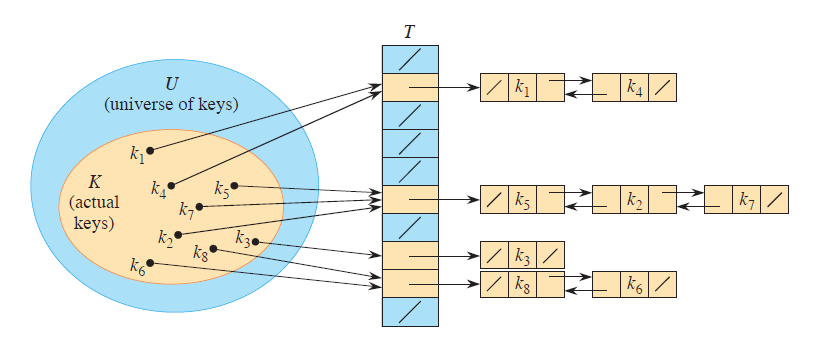
当关键字的全域范围 $U$ 不大的时候（比如 $U = \{ x \mid x \in \mathbb{Z} \text{ and } x \leq 100\}$），且键不重复，直接寻址是简单且高效的。

通常可以用一个数组（或称直接寻址表）来表示一个动态的集合，记作 $T[0..m-1]$。每一个下标（slot）都对应着 $U$ 当中的一个键。

如图，$U$ 很小，$U$ 当中所有元素都对应着数组 $T$ 当中的一个位置。数组 $T$ 的每一个元素保存了键值对，或是空的：

对于直接寻址表，查找、插入、删除，都很简单，都是 $O(1)$ 的，伪代码如下：

然而，如果 $U$ 非常大，比如 $U = \mathbb{Z}$，这种情况下，就无法使用直接寻址表了，因为内存不够。

但是，有一种可能的情况：$U$ 很大，但实际存在的键的集合 $K$ 不大。那么，实际需要的内存，可能只是 $\Theta(|K|)$ 的。这也避免了空间的浪费。

哈希表 hash table

哈希表就是，存储空间只需要 $\Theta(|K|)$，而效率仍然是 $O(1)$。

在直接寻址表当中，关键字 $k$ 对应的元素，放在下标 $k$ 的位置上；在哈希表当中，它在 $h(k)$ 的位置上。其中，$h:U \rightarrow \{0,1, \cdots, m-1\}$ 是哈希函数。这个 $m$ 相对于 $U$ 通常是非常小的。可以说 $h(k)$ 就是键 $k$ 的哈希值。

但是如果哈希函数 $h(k)$ 设计的不好，可能会发生哈希 冲突（collision）。举个例子，假如 $h(x) = x^2$，那么对于键 $k_1 = -1$ 与 $k_2 = 1$，$h(k_1) = h(k_2) = 1$，他俩的哈希值相等。这样就会导致，这俩不同的键，映射到了同一个位置。

我们希望哈希冲突不存在，但这是不可能的，因为 $|U| > m$，根据抽屉原理，至少有两个键的哈希值相等。所以只能通过精心设计哈希函数，尽量的减少哈希冲突。然后找到一种方法，解决这种冲突。

链接法（chaining）

预备知识：实现链表的插入、查找、删除

这里的链表，就当他是双向的。

元素插入到头部：$O(1)$

已知键，查找元素：$\Theta(n)$

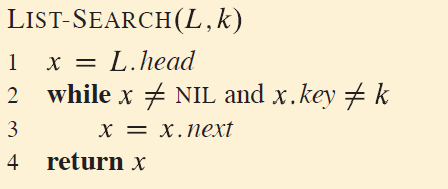
已知键值对，删除元素：$O(1)$

假如只知道键，那就需要先查找到再删除了。

链接法的思想

也有的教材管这个叫做「十字链表法」。这是最简单的解决哈希冲突的方式。

链接法的思想是，每个位置，都是一个指向链表的指针。如果这个位置没有元素，那么这个指针就是空指针；如果有，就指向一个链表，这个链表保存了所有的被哈希到这个位置的元素。

这个链表可以是单链表（singly），也可以是双向链表（doubly）。下面图示当中的是双向链表，因为双向链表的删除操作更快。至于为什么更快，稍后分析。

链接法的实现

插入

插入是 $O(1)$ 的。因为插入是可以插在链表头部，而不是尾部，无需遍历链表。

查找

最坏情况下的效率是 $O(n)$，这里的 $n$ 指的是链表长度。

删除

双向链表删除元素是 $O(1)$ 的（假设已查找过），因为删除元素的函数，参数是 x 而不是 k，这个 x 包含了前驱节点、后继结点的位置，所以只需要执行：T[x.prePos].nextPos = x.nextPos 和 T[x.nextPos].prePos = x.prePos 即可实现删除。

对于单链表，如果要删除的元素不在链表的两端而在中间，就需要先找到前驱再修改前驱，这需要一次遍历，所以可能会很慢。

链接法的性能分析

插入删除都是 $O(1)$，性能瓶颈在于查找，所以下面主要分析查找的性能。

假设哈希表 $T$ 一共具有 $m$ 个 slot、一共有 $n$ 个元素需要插入表中。定义 $T$ 的 装载因子（load factor） 为 $\alpha = \frac{n}{m}$，即每个链的平均元素数量。

假设，每一个元素被哈希函数映射到每一个位置上的概率都是相等的，且每个元素的映射都相互独立，即：简单均匀散列（simple uniform hashing）。

用 $n_j$ 表示第 $j$ 个链表的长度。那么，$n = \sum_{j=0}^{m-1} n_j$ 且 $E(n_j) = \alpha$.

在一个链表当中寻找键 $k$ 的元素，结果只有两种可能：要么找到了，要么没找到。

有两个定理

对于简单均匀散列的链接法，没找到，平均时间复杂度是 $\Theta(1 + \alpha)$
对于简单均匀散列的链接法，找到了，平均时间复杂度是 $\Theta(1 + \alpha)$

下面分别证明。

证明：简单均匀散列，链接法，没找到，平均时间复杂度是 $\Theta(1 + \alpha)$

没找到，那就意味着要从表头一直遍历到末尾，那么所花费的时间就跟链表的长度有关。由于 $h(k)$ 均匀地映射到 $m$ 个位置，而 $m$ 个位置的平均长度是 $\alpha$，所以不成功的查找，加上计算哈希函数的消耗，所需平均时间复杂度是 $\Theta(1 + \alpha)$。

证明：简单均匀散列，链接法，找到了，平均时间复杂度是 $\Theta(1 + \alpha)$

预备知识：指示器随机变量 indicator random variable

给定一个样本空间 $S$ 和一个事件 $A$，那么事件 $A$ 对应的指示器随机变量 $\mathrm{I}\{A\}$ 定义为：$$\mathrm{I}\{A\} = \begin{cases} 1 & \text{事件 } A \text{ 发生} \\ 0 & \text{事件 } A \text{ 未发生}\end{cases}$$。

引理：一个事件 $A$ 对应的指示器随机变量的期望值，等于事件 $A$ 发生的概率。证明很简单，略。

举个例子来理解这个引理。抛硬币。要计算正面朝上的次数。样本空间为 $S = {H, T}$，且 $P(H) = P(T) = 0.5$. 然后定义指示器随机变量 $X_H$ 对应于正面朝上的事件 $H$。这个变量有统计正面朝上次数的作用：$$\begin{aligned} X_H & =\mathrm{I}\{H\} \\ & = \begin{cases}1 & \text {事件 } H \text { 发生} \\ 0 & \text {事件 } T \text { 发生}\end{cases} \end{aligned}$$。那么抛一次硬币正面朝上的期望的次数，就是 $X_H$ 的期望值。根据期望的定义，有：$$\begin{aligned} E(X_H) & = E(\mathrm{I}\{H\}) \\ &= 1 \cdot P(H) + 0 \cdot P(T) \\ & =1 \cdot 0.5 +0 \cdot 0.5 \\ &= 0.5 \\ &= P(H)\end{aligned}$$。

证明开始

假设，$n$ 个元素每个被查找的概率都相等。找到了元素 $e$，那么遍历的链表长度，就是链表中 $e$ 前面的元素的个数加上一，也就是该链表中比 $e$ 后插入的元素的数量 加上一。

设 $e_i$ 表示第 $i$ 个被插入的元素，$k_i$ 表示 $e_i$ 的键。

设事件 $A$ 表示元素 $e_i$ 与 $e_j$ 的键的哈希值相等，即 $A = (h(k_i) = h(k_j))$。因为我们假设是简单均匀散列，所以 $P(A) = \frac{1}{m}$。

定义指示器随机变量 $X_{ij} = \mathrm{I}{A}$，于是根据刚刚的引理得到 $E(X_{ij}) = P(A) = \frac{1}{m}$。

所以就可以列式表达出，如果找到了，所遍历的元素的数目的期望值： $$\begin{aligned}E\left(\frac{1}{n}\sum_{i=1}^n\left(1+\sum_{j=i+1}^nX_{ij}\right)\right) &= \frac{1}{n}\sum_{i=1}^n\left(1+\sum_{j=i+1}^nE(X_{ij})\right) \\ &= \frac{1}{n}\sum_{i=1}^n\left(1+\sum_{j=i+1}^n\frac{1}{m}\right) \\ &=\frac{1}{n}\sum_{i=1}^n+\frac{1}{n}\sum_{i=1}^n\left(\sum_{j=i+1}^n\frac{1}{m}\right) \\ &= \frac{1}{n}\sum_{i=1}^n+\frac{1}{m}\sum_{i=1}^n\left(\sum_{j=i+1}^n\frac{1}{n}\right) \\ &= \frac{1}{n}\sum_{i=1}^n+\frac{1}{m}\sum_{i=1}^n\left((n-i)\frac{1}{n}\right) \\ &= 1+\frac{1}{nm}\sum_{i=1}^n(n-i) \\ &= 1+\frac{1}{nm}\left(\sum_{i=1}^nn-\sum_{i=1}^ni\right) \\ &= 1+\frac{1}{nm}\left(n^2-\frac{n(n+1)}{2}\right) \\ &= 1+\frac{n-1}{2m} \\ &=1+\frac{n}{2m}-\frac{1}{2m} \\ &= 1+\frac{n}{2m}-\frac{n}{2mn} \\ &= 1+\frac{\alpha}{2}-\frac{\alpha}{2n}\end{aligned}$$ ，所以再加上计算哈希函数所需的消耗，平均时间复杂度是 $$\Theta(2 + \frac{\alpha}{2} - \frac{\alpha}{2n}) = \Theta(1 + \alpha)$$。

那么 $\alpha$ 的规模是多大？

如果 $m$ 至少与 $n$ 成正比，即 $m = \Omega(n)$ 即 $n = O(m)$，那么就有 $$\alpha = \frac{n}{m} = \frac{O(m)}{m} = O(1)$$！

假如再采用双向链表实现，那么，插入、查找、删除，所有操作时间复杂度都是 $O(1)$ 的！

哈希函数 hash function

一个好的哈希函数应当尽可能地满足简单均匀散列，同时最小化相似关键字被散列到相同位置的概率。

一般哈希函数都假定键的全域是自然数集 $\mathbb{N}$。所以如果键是字符串，要想办法把它转换成整数。比如字符串可以当作 128 进制的一个数字。

除法哈希法 division method

简单，也很快：$h(k) = k \bmod m$。

但是 $m$ 的取值，也是有讲究的。比如，$m$ 不能取 $2$ 的幂。因为这种情况下，$k \bmod m$ 相当于取 $k$ 的前 $p$ 位二进制位，容易造成哈希冲突。

通常，$m$ 应当选择 不接近 $2$ 的整数幂的素数。比如，假如 $n = 2000$，可以接受平均每次「找不到」要遍历 $3$ 个元素，那么 $m = 701$ 就是一个不错的选择。

乘法哈希法 multiplication method

$h(k) = \lfloor m\left(kA - \lfloor kA \rfloor\right) \rfloor$，即 $m$ 乘上 $kA$ 的小数部分再向下取整。其中，$0 < A < 1$ 是个常数。

乘法散列法的优点是，$m$ 的值的选取不是很重要。一般 $m$ 会选取为 $2$ 的整数幂，具体原理可以查阅算导。

全域哈希法 universal hashing

假如有一个大坏蛋，提前知道了程序使用的哈希函数，那么他就可以故意构造一组数据，制造大量的哈希冲突，使每一次查找都退化成 $O(n)$。

全域散列法是解决这个问题的唯一办法：设计多个哈希函数，随机从中选择一个使用。这样就可以确保对于任何输入，都能具有较好的平均性能。

对于一组将 $U$ 映射到 $[0, m-1] \cap \mathbb{Z}$ 的哈希函数，如果满足如下条件，则称 $\mathcal{H}$ 是 全域（universal） 的：对于每一对不同的键 $k, l \in U$，满足 $h(k) = h(l)$ 的散列函数 $h \in \mathcal{H}$ 的个数不超过 $\frac{\mathcal{H}}{m}$. 换句话说就是，随机选取一个哈希函数 $h \in \mathcal{H}$，当键 $k \neq l$ 时，二者发生哈希冲突的概率不超过 $\frac{1}{m}$，而 $\frac{1}{m}$ 恰恰是直接从集合 $[0, m-1] \cap \mathbb{Z}$ 当中选取两个位置相同的概率。

全域哈希的性能

有定理表明，如果 $h$ 选自一组全域哈希函数，将 $n$ 个键映射到大小是 $m$ 的表 $T$ 当中，$\alpha = \frac{n}{m}$，用链接法解决哈希冲突：

若 $k$ 不在表中，则 $k$ 被散列到其中的链表的期望长度 $E(n_{h(k)})$ 不超过 $\alpha$
若 $k$ 在表中，包含 $k$ 的链表的期望长度不超过 $\alpha + 1$

这个定理课件上没有证明。

设计一个全域哈希函数类

选取一个足够大的素数 $p$，使得每一个可能的键都位于 $[0, p-1]$ 范围内，因此 $p > m$
设集合 $\mathbb{Z}_P = \{0, 1, 2, \cdots, p-1\}$，$\mathbb{Z}_P^* = \{1, 2, 3, \cdots, n-1\}$
对于 $\forall a\in \mathbb{Z}_P$ 和 $\forall b \in \mathbb{Z}_P^*$，定义哈希函数 $h_{a,b}(k) = ((ak+b)\bmod p)\bmod m$；例如当 $p, m = 17, 6$ 则 $h_{3,4}(8)=5$
所有这样的哈希函数构成了一个簇（family）$$\mathcal{H}_{p,m} = \{h_{a,b} \mid a \in \mathbb{Z}_P, b \in \mathbb{Z}_P^*\}$$，这个簇当中共有 $p(p-1)$ 个哈希函数，每个函数 $h_{a,b}$ 都将 $\mathbb{Z}_P$ 映射到 $\mathbb{Z}_m$。
这类哈希函数还有一个很好的性质就是，$m$ 不必是素数

开放寻址法 open addressing

开放寻址法的意思是，所有的元素都存储在哈希表里面，而不是存在外部的某个链表再从哈希表查找这个链表的地址。不用指针 是开放寻址法的一大优点。不用指针就可以节省内存，节省了内存就可以开更大的表，表变大了那么产生冲突的概率也会变小。

因此，使用开放寻址法，整个哈希表可能会被填满，从而一定有 $\alpha \leq 1$。

修改哈希函数

使用开放寻址法，为了找到可以插入元素的位置，需要对哈希表进行遍历，查找空的位置。这个过程叫做 探查（probe）。

探查的顺序当然不是 $0, 1, 2, \cdots, m-1$——这样效率太低了。因此探查的顺序应当与键有关。

于是，我们把之前的哈希函数 $h(k)$ 扩展成二元函数 $h(k, i)$，表示对关键字 $k$ 执行插入，第 $i+1$ 次探查的位置在哪里：$$h: U \times\{0,1, \cdots, m-1\} \rightarrow\{0,1, \cdots, m-1\}$$，它的输出依然是 $m$ 个位置之一。那么根据上述定义，对于键 $k$，探查序列就是 $$\left[ h(k,0), h(k,1), \cdots, h(k,m-1) \right]$$，这恰恰是 $0 \sim m-1$ 的一个排列。如果哈希表快填满了，那么 $h(c,i)$ 当中的 $i$ 就难免比较大，排列意味着每个位置都有概率被插入，不会出现表还没满却不知道插哪里的情况。

实现：基于开放寻址法的插入查找删除

插入

返回实际插入的位置，或空间已满，返回一条错误信息：

查找

返回键 $k$ 对应元素所在的位置。如果未找到，则返回 NIL。

关于删除

代码很简单，略。但是要注意：

不能把要删除的位置的值设置为 NIL。如果设置成了 NIL，那么有可能会导致，接下来查找某个元素的时候，探查到了该位置发现是 NIL，程序直接认为键不存在而返回，实际上它在后面。
因此，要把需要删除的位置设置成 DEL。此外，执行插入的代码，那行 if 要改成：if T[q] == NIL or T[q] == DEL。查找的代码无需改动。

探查方案

开放寻址法最主要的问题是如何计算哈希函数。有三种常用的方法，然而都不是均匀散列的（均匀散列要求所有的探查序列都可能产生，也就是说均匀散列要求产生 $m!$ 个不同的探查序列）。

线性探查 linear probe

设一个普通的哈希函数 $h^\prime: U \rightarrow \{0, 1, 2, \cdots m-1 \}$，这里管它叫做辅助函数（auxiliary function）。那么，线性探查的哈希函数是：$$h(k, i) = (h^\prime(k) + i) \bmod m$$。显然，这种函数对每个键产生的探查序列都是从 $h^\prime(k)$ 开始的连续 $m$ 个位置，也就是说它的序列完全由 $h^\prime(k)$ 决定。

因此，线性探查只能产生 $m$ 个不同的探查序列。故，它不是均匀散列的。

然而线性探查还有一个比较影响效率的问题：一次群集（primary clustering）。因为一个空的位置前面，假如已经有了连续的 $i$ 个非空的位置，那么插入到这个空的位置的概率是 $\frac{i+1}{m}$，这个概率随 $i$ 增大而增大。也就是说，表越满，查找就越慢。

二次探查 quadratic probe

二次探查除了使用到了一个辅助函数，还用到了两个正常数 $c_1, c_2$：$$h(k,i) = (h^\prime(k) + c_1i + c_2i^2) \bmod m$$，显然，$h(k_1, 0) = h(k_2, 0) \Rightarrow h(k_1, i) = h(k_2, i)$。因此，二次探查的哈希函数所产生的探查序列，也是由第一个决定的。

因此，二次探查也是只能产生 $m$ 个不同的探查序列，它也不是均匀散列的。

由于 $h(k_1, 0) = h(k_2, 0) \Rightarrow h(k_1, i) = h(k_2, i)$，二次探查可能也会导致一些轻度的群集，称为 二次群集（secondary clustering）。

双哈希 double hashing

双哈希使用两个辅助函数。它的哈希函数是：$$h(k,i) = (h_1(k) + ih_2(k)) \bmod m$$。由于 $ih_2(k)$ 的存在，显然双哈希产生的探查序列，不仅仅依赖于探查序列的第一个位置。因此，它产生的探查序列的总数不止 $m$ 个。

在数学性质上，为了能覆盖整个哈希表，$h_2(k)$ 的值必须与表的大小 $m$ 互素。有两种简单的实现方式：

令 $m$ 是 $2$ 的幂（质因子只有 $2$），令 $h_2(k)$ 是奇数（质因子不含 $2$），这样一定是互素的
令 $m$ 是一个质数（质因子只有自身），令 $h_2(k)$ 是不超过 $m$ 的任意数，这样也一定可以让它们互素

这两种方案都可以产生 $\Theta(m^2)$ 种不同的探查序列。比一次和二次探查好不少。