跳转至

Chapter 2 Part 3: 卡诺图

（共 41 页）

在线画图圈圈网站：http://32x8.com/

格雷码

这部分考试应该不会太细，主要是在格雷码里面的标号。

格雷码是一个二进制数系，其中两个相邻数的二进制位只有一位不同。如，三位以内的格雷码是：

十进制 格雷码 二进制
0 0 0
1 1 1
2 11 10
3 10 11
4 110 100
5 111 101
6 101 110
7 100 111

手动构造

$k$ 位的格雷码可以通过以下方法构造。我们从全 $0$ 格雷码开始，按照下面策略：

  1. 翻转最低位得到下一个格雷码，（例如 $000\to 001$）；
  2. 把最右边的 $1$ 的左边的位翻转得到下一个格雷码，（例如 $001\to 011$）；

交替按照上述策略生成 $2^{k-1}$ 次，可得到 $k$ 位的格雷码序列。

镜像构造

$k$ 位的格雷码可以从 $k-1$ 位的格雷码以上下镜射后加上新位的方式快速得到，如下：

image-20230329215540649

二进制数转格雷码

（假设以二进制为 0 的值做为格雷码的 0）

$G$：格雷码；$B$：二进制码；$n$：正在计算的位

根据格雷码的定义可得：$G(n) = B(n+1) \oplus B(n)$，即 $G(n) = B(n+1) + B(n)$。

自低位至高位运算即可，无需考虑进位。

计算方法

观察一下 $n$ 的二进制和 $G(n)$。可以发现，如果 $G(n)$ 的二进制第 $i$ 位为 $1$，仅当 $n$ 的二进制第 $i$ 位为 $1$，第 $i+1$ 位为 $0$ 或者第 $i$ 位为 $0$，第 $i+1$ 位为 $1$。于是我们可以当成一个异或的运算，即 $G(n)=n\oplus \left\lfloor\frac{n}{2}\right\rfloor$

int g(int n) { return n ^ (n >> 1); }

通过格雷码构造原数（逆变换）

接下来考虑格雷码的逆变换，即给定一个格雷码 $g$，要求找到原数 $n$。我们考虑从二进制最高位遍历到最低位（最低位下标为 $1$，即个位；最高位下标为 $k$）。则 $n$ 的二进制第 $i$ 位与 $g$ 的二进制第 $i$ 位 $g_i$ 的关系如下：

$$\begin{array}{rll} n_k &= g_k \\ n_{k-1} &= g_{k-1} \oplus n_k &= g_k \oplus g_{k-1} \\ n_{k-2} &= g_{k-2} \oplus n_{k-1} &= g_k \oplus g_{k-1} \oplus g_{k-2} \\ n_{k-3} &= g_{k-3} \oplus n_{k-2} &= g_k \oplus g_{k-1} \oplus g_{k-2} \oplus g_{k-3} \\ &\vdots\\ n_{k-i} &=\displaystyle\bigoplus_{j=0}^ig_{k-j} \end{array}$$

int rev_g(int g) {
  int n = 0;
  for (; g; g >>= 1) n ^= g;
  return n;
}

卡诺图

卡诺图是用 2D 形式表示的多维函数。

EE103 部分笔记

卡诺图一共有 $2^n$ 个小格，每个小格子都存储一个最小项，小格之间按照 格雷码 排列，即保证了最小项之间 逻辑相邻 以及 几何相邻。
其中，几何相邻包括三种：内相邻（紧挨着）、外相邻（一行或一列的两头）、中心对称~~（一直不是很懂中心对称指什么，CS220 说只有内外相邻两种）~~

下图可以直观体现出卡诺图的几何相邻：

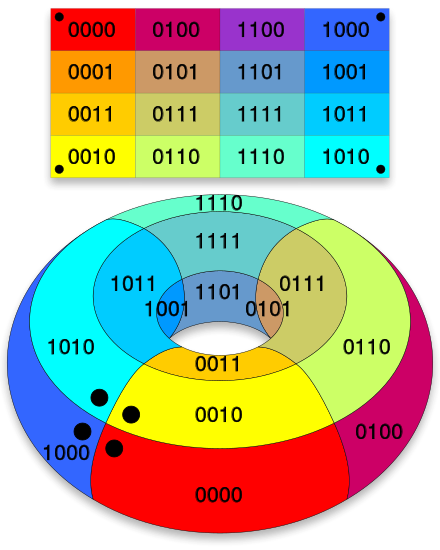
卡诺图画相邻圈时，应使每个圈包含 $2^n$ 个格子，且圈圈要尽量大。

下表是可选的卡诺图每个小格的排列样式。

C'D' C'D CD CD'
A'B' 0 1 3 2
A'B 4 5 7 6
AB 12 13 15 14
AB' 8 9 11 10

五变量卡诺图较为麻烦，可使用重叠画法。

一些新概念

注意：卡诺图当中的乘积项，一定是大小为 2 的幂的一个圈。

  • 涵项（implicant），是一个乘积项，可以被写进 SOP 形式当中的那种乘积项（可以被圈圈的格子）。注意不一定是最小 SOP。只要这个值对应 1，就是 Implicant。
  • 布尔函数 $F$ 的 质涵项（prime implicant），是 最少化文字数量 的涵项——就是说，如果从一个乘积项 $P$ 去除任何「文字 literal」都导致 $P$ 成为布尔函数 $F$ 的非涵项，那么这个乘积项就是质涵项。例如 $AB'C'$ 和 $AB'C$ 现在是某逻辑函数的两个涵项，那么 $AC$ 就是函数的一个质涵项，其中的 $A$ 和 $C$ 不可再去掉。而最小化文字数量，意味着尽量圈的圆圈大一点。
  • 基本质涵项（essential prime implicant），是一种特殊的质涵项，是 蕴涵于不满足任何其他质涵项的最小项的 那些质涵项。换句话说，若存在只被一个质涵项覆盖的极小项，则覆盖该极小项的质涵项为基本质涵项。如果以卡诺图的形式来描述逻辑函数，可以发现只有一种方式可以圈选这个输入组合。

结合课件 24 页左右的例子可能比较容易理解。

卡诺图中找 PI 和 EPI 的规律总结（个人心得）

感觉，找 PI，就是执行下面几个步骤：

  1. 对于每一个没被圈的最小项格子，看能不能圈大小是 16 的？能，所有方案都圈出来，break。
  2. 对于每一个没被圈的最小项格子，看能不能圈大小是 8 的？能，所有方案都圈出来，break。
  3. 对于每一个没被圈的最小项格子，看能不能圈大小是 4 的？能，所有方案都圈出来，break。
  4. 对于每一个没被圈的最小项格子，看能不能圈大小是 2 的？能，所有方案都圈出来，break。
  5. 对于每一个没被圈的最小项格子，看只能圈大小是 1 的了。

对于 EPI，就是找到所有 PI 之后，依次检查每一个最小项，如果这个最小项只被一个圆圈圈起来了，那么这个圈就是 EPI。

不关心项（无关项） Don't care term

DCT 在卡诺图当中，指无论取 0 还是取 1，对结果没有影响，无所谓。在实际应用中，可能是因为，这个位置的变量取值组合，永远不会出现。