Chapter 7 关于均值的推断
只知道样本的,不知道总体的,用样本的对总体的进行推断和估计。
The two main classes of statistical inference are estimation of parameters and testing hypotheses(参数估计(包括点估计、区间估计)、假设检验)
点估计:均值
根据 $X_1, X_2, \cdots, X_n$,可以得到 $\overline X$,这个值就是估计的总体均值 $\mu$,这个估计的标准误差是 $\frac{s}{\sqrt n}$。
最大估计误差 maximum error of estimate
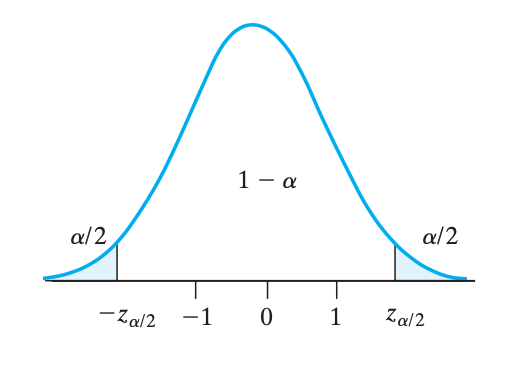
根据中心极限定理,有 $$Z=\frac{\overline X - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)$$。要让服从标准正态分布的 $Z$ 落在区间 $[-z_{\alpha/2}, z_{\alpha/2}]$ 内,通过化简得到:$$\left|\overline X - \mu\right| \leq z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}}$$,于是,$$\boxed{E = z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}}}$$,即 $$\mu-E \leq \overline X \leq \mu+E$$。
二级结论:$\sigma$ 未知的情况
如果 $\sigma$ 未知且 $n$ 比较大,那直接用 $s$ 代替 $\sigma$ 就好了。但是如果 $n$ 不是很大,也可以用 $s$ 代替 $\sigma$,但是要把 $z$ 分位点改成 $t$ 分位点:$$E = t_{\alpha/2}\cdot\frac{s}{\sqrt{n}}$$。
二级结论:样本要多大?
要满足 $P(|\overline X - \mu| < E) = 1-\alpha$,需要满足样本大小 $n$,把之前 $E$ 的公式移项化简一下,得到 $n$ 至少要是:$$n_{\min} = \left(\frac{\sigma\cdot z_{\alpha/2}}{E}\right)^2$$。
无偏估计
无偏性、有效性
知道有这么回事儿就行了(稀里糊涂的)
当且仅当 $E(\hat\theta) = \theta$ 则称这个 $\theta$ 的估计是无偏的,其中 $\hat\theta$ 表示估计量,即对 $\theta$ 的估计值。大概意思就是估计的值恰好就是真实值,比如 $E(\overline X) = \mu$
若有两个估计都是无偏的,那么方差小的那个就是 更好(more efficient) 的。
区间估计:均值
置信区间 confidence interval
对于较大($n\geq30$)的样本,若总体标准差 $\sigma$ 已知,则 $(1-\alpha)100\%$ 的置信区间是:$$\boxed{\left(\bar{X}-z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}, \quad \bar{X}+z_{\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}\right)}$$。换句话说就是,$\mu$ 落在这个区间里面的概率是 $1-\alpha$。
如果总体标准差 $\sigma$ 未知,且样本较大,可以用样本标准差 $s$ 代替。
如果总体标准差 $\sigma$ 未知,且样本不够大($n<30$),用样本标准差 $s$ 代替之后,还要把正态分布 $z$ 换成 $t$:$$\left(\bar{X}-t_{\alpha / 2} \cdot \frac{s}{\sqrt{n}}, \bar{X}+t_{\alpha / 2} \cdot \frac{s}{\sqrt{n}}\right)$$。
极大似然估计 maximum likelihood estimate
只要出现了,极大似然估计就认为,这个出现的概率很高。
从简单例子开始:抛硬币
假如有一个硬币(不一定均匀),抛出四次,三次正面朝上。设单次正面朝上的概率是 $p$。
根据伯努利分布,三次正面朝上的概率是 $4p^3(1-p)^1$,把这个函数的图像画出来
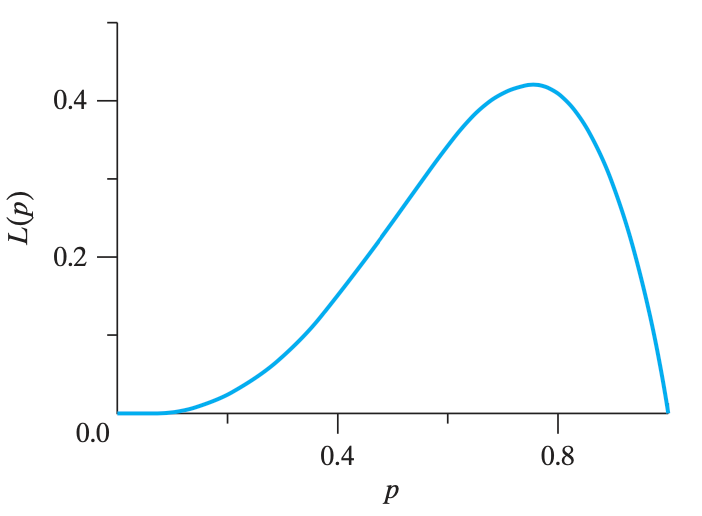
极大似然估计就是,找出这个函数图像最大值(求导之后就知道最大值是多少了)。最大值对应的点,就是估计的 $p$ 的值(在本题中,$\hat p=0.75$)
更一般的情况
有一个跟参数 $\theta$ 相关的概率密度函数 $f(x;\theta)$,($\theta$ 就像是刚刚例子里面的 $p$)。
把 $X_i$ 分别代入 $x_i$,用函数 $f$ 再构造一个极大似然函数 $L$:$$L\left(\theta \mid x_1, \cdots, x_n\right)=\prod_{i=1}^n f\left(x_i ; \theta\right)$$,极大似然估计就是指,找到一个 $\theta$ 的取值,让这个函数 $L$ (一堆 $f$ 的乘积)取得极大值。
~~没太懂。会做题就行~~
例子:再抛一次硬币
进行了 $n$ 次抛硬币,每次都是 $p$ 的概率正面朝上。第 $i$ 次是否朝上,用随机变量 $X_i$ 表示:$$P\left[X_i=0\right]=1-p, \quad P\left[X_i=1\right]=p$$,然后左右两个式子合起来,变成了 $$P(X_i=a)=p^a(1-p)^{1-a}$$,代入极大似然函数 $L$,得到 $$L(p\mid x_1,\cdots,x_n)=p^{x_1+x_2+\cdots+x_n}\times(1-p)^{n-(x_1+\cdots+x_n)}$$,现在就是要找到一个 $\hat p$,使 $L$ 取到最大值。由于有幂次,这个函数 取对数之后再求导 比较好算。令取对数后的导数等于零:$$\frac{x_1+\cdots+x_n}{p}-\frac{n-(x_1+\cdots+x_n)}{1-p}=0$$,最终能得到 $\hat p = \frac{x_1+\cdots+x_n}{n}$ 使函数 $L$ 最大。
- Note 1: 这里极大似然估计的对象是 $p$,而不是 $x$
- Note 2: 巧合的是,课件上给出的例题(7.8~7.13)几乎算出来答案都是 $\frac{x_1+\cdots+x_n}{n}$
二级结论
- 对于正态分布,$\hat\mu = \frac{1}{n}(x_1+x_1+\cdots+x_n)$,$\hat\sigma^2 = \frac{1}{n}\sum_{i=1}^n(x_i-\mu)^2$,具体的推导过程可以看例子 7.10 和例子 7.11
- 若 $\hat\theta$ 是 $\theta$ 的极大似然估计,有一个 one-to-one 的函数 $g$,而那么 $g(\hat\theta)$ 就是 $g(\theta)$ 的极大似然估计
假设检验
- 第一类错误,就是原本假设是对的,但拒绝了(主要讨论这一类)
- 第二类错误,就是原本假设是错的,但没拒绝(牵涉真实值,反正比较复杂,参考课件 24 页的图)
发生第一类错误的概率,也叫做 显著性水平(level of significance),通常 $\alpha=0.05$ 或 $\alpha=0.01$,看题目指定。
两类错误是跷跷板的关系,一类的概率大,另一类概率就会小。
假设检验步骤
- 确定好原假设和备选假设
- 说明显著性水平
- 基于样本的分布,构造一个关于原假设和备选假设的判别
- 计算出决策所依据的统计量的值
- 决定是否拒绝假设
注意,原假设不能用「接受」这个词,而应该说「不能拒绝」
原假设 null hypothesis
- 用 $H_0$ 表示
- 还有个叫做 备选假设 alternative hypothesis 的东西,总是与原假设成对出现
- 一旦原假设被拒绝,就认为备选假设成立
- 备选假设有两种,单边假设(one-sided)与双边假设(two-sided)
- 单边就是大于或小于
- 双边就是不等于
对于原假设 $\mu = \mu_0$ 以及 $Z = \frac{\mu-\mu_0}{\frac{\sigma}{\sqrt{n}}}$,可以得出这样一个表格:
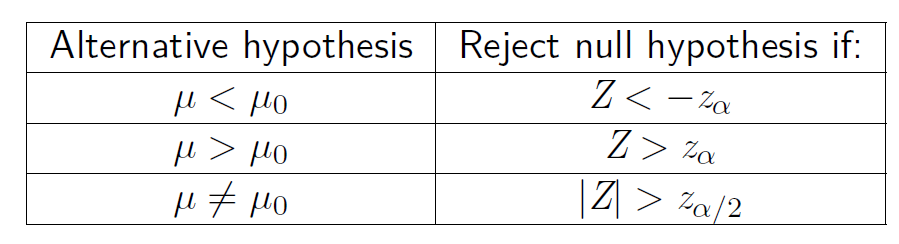
结合例子比较好理解
选取原假设的 guidelines
若一个实验的目标,是建立一个断言,那么原假设应该选取为,断言的否定;备选假设应该是该断言。
P 值
P 值(P value)就是 当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率。说白了就是分位点后面的面积呗。
注意看清楚是单边假设还是双边假设。
用处:$P \leq \alpha$ 则拒绝原假设,否则不拒绝原假设。
例题 7.16
首先算出来 $Z = \frac{\bar x - 71}{(s / \sqrt{80}} = -2.38$,这是必须步骤
法一
根据显著性水平算出来那个边界 -2.326(=NORM.S.INV(0.01)),然后 Z 比这个边界更小,所以拒绝原假设
法二
计算 P-value,算出来 P 值约为 0.0086(norm.s.dist(-2.38, true)),小于显著性水平 0.01,所以拒绝原假设