Chapter 6 样本分布

随机样本

随机样本有两类，一类是从有限的总体当中随机抽的，另一类是是从无限总体当中随机抽的。不管总体是有限的还是无限的，假设样本大小是 $n$，样本当中每个 $X_i$ 都是独立的，且服从总体的分布。

可以说「分布函数 $F$」，也可以说「总体 $F$」，也可以说「总体 $X$」。

定理：若一个大小为 $n$ 随机样本是从一个均值为 $\mu$、方差是 $\sigma^2$ 的总体当中抽出来的，那么这个 样本的平均值，也是 $\mu$，但是方差要分情况：

若总体无限，方差是 $\frac{\sigma^2}{n}$
若总体有限，方差是 $\frac{\sigma^2}{n}\frac{N-n}{N-1}$，其中 $\frac{N-n}{N-1}$ 叫做 校正因子（finite population correction factor）

大数定律 law of large numbers

一般用 $\mu$ 表示整体的平均，$\overline X$ 表示样本的平均。

一堆独立的随机变量 $X_1, X_2, \cdots, X_n$，如果 $n$ 充分大，那么测出来的平均值和实际平均值存在偏差的概率就是零。即对于 $\forall \epsilon>0$，有 $$P(|\overline{X}-\mu|>\epsilon) \to 0,\qquad n\to \infty$$

中心极限定理 Central limit theorem（要求 $\sigma$ 已知）

有一个均值为 $\mu$、方差是 $\sigma^2$ 的总体，从中搞一个样本出来，若样本均值是 $\overline{X}$，则标准化后的样本均值 standardized sample mean 是 $$Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}$$，当 $n$ 足够大，这个 $Z$ 就服从标准正态分布（做题的时候一般 $n\geq25$ 就是了）

$Z$ 的分母里面是 $Var(\overline{X})$ 开根号。也就是说，$\overline{X} \sim N\left(\mu, \left(\frac{\sigma}{\sqrt{n}}\right)^2\right)$。

注意：这里的正态分布，标准差是样本的，而不是原始总体的！

就是说，计算一个平均值（$\overline{X}$）满足的分布，很难（因为即使是 $X$ 的分布都不一定能算）。由于不太关心精确值，$n$ 充分大的时候，尽管精确表达式不知道，就可以用正态分布去很好的逼近，所以直接用正态分布算就行了。前提是原始的方差 $\sigma$ 已知。

顺带一提，如果原始数据本身（总体）就已经服从正态分布了，那么随机样本还是服从正态分布的。即：若总体不是正态分布，只有 $n$ 足够大的时候样本才接近正态分布；总体服从正态分布，无论 $n$ 多大样本都服从正态分布。

t-分布：$\sigma$ 未知，但 $\mu$ 已知

$\overline{X}$ 是从一个服从 $N(\mu,\sigma^2)$ 的 正态分布的总体（$\sigma$ 未知）当中抽出来的样本的均值，且 $S = \sqrt{\sum\frac{(X_i-\overline{X})^2}{n-1}}$ 是样本的标准差，那么 $$t=\frac{\overline{X}-\mu}{\frac{S}{\sqrt{n}}}$$，这个 $t$ 就服从参数（自由度）为 $\nu=n-1$ 的 t-分布。

$t$ 的概率密度函数长得很复杂：$$p_t(y)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n \pi} \Gamma\left(\frac{n}{2}\right)}\left(1+\frac{y^2}{n}\right)^{-\frac{n+1}{2}}, \quad y \in \mathbb{R}$$。

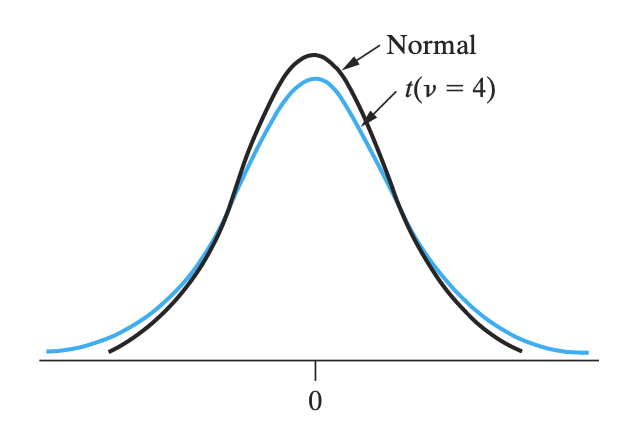
t-分布的性质

t-分布的形状左右对称
t-分布的尾巴比正态分布的大，意味着不太集中（发散），也就是方差大一些
若 $n>1$，则 t-分布的均值是零（对称轴）
若 $n>2$，则 t-分布的方差是 $\frac{n}{n-2}$
当 $n$ 足够大（一般 $n \geq 30$），则 t-分布非常接近正态分布
在实际上，t-分布假设了总体是服从正态分布的，但是严格正态分布可能比较难。所以基本上是正态分布的也可以用 t-分布。

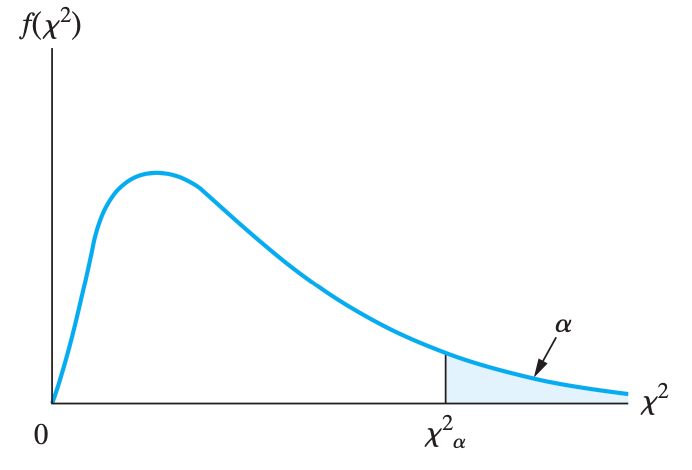
卡方分布 chi-square：$\sigma$ 已知，不关心 $\mu$

设 $S^2$ 是一个从服从方差为 $\sigma^2$ 的 正态分布的总体 当中抽取的大小为 $n$ 的样本的方差。那么 $$\chi^2=\frac{(n-1) S^2}{\sigma^2}=\frac{\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}{\sigma^2}$$，这个变量 $\chi^2$ 就服从参数自由度为 $v=n-1$ 的 chi-square 分布。

$$p(y)=\frac{(1 / 2)^{\frac{n}{2}}}{\Gamma(n / 2)} y^{\frac{n}{2}-1} e^{-\frac{y}{2}}, \quad y \geq 0$$

卡方分布是 $\alpha=\frac{\nu}{2}$,$\beta=2$ 的伽马分布的特例。

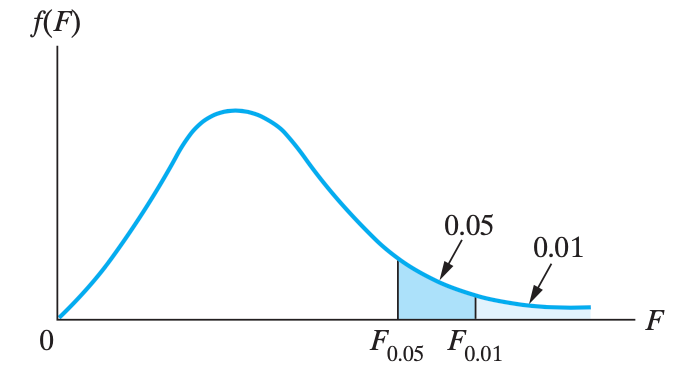
F 分布：用于检查两个总体的 $\sigma$ 是否相同

若从 方差相等但未知的服从正态分布的两个总体 当中，分别抽取两个大小为 $n_1$, $n_2$ 的样本。设两个样本方差分别是 $S_1^2$, $S_2^2$，那么 $F = \frac{S_1^2}{S_2^2}$ 就是一个服从参数为 $\nu_1=\nu_2=n-1$ 的 F 分布的随机变量。

F 分布的概率密度函数是 $$p(y)=\frac{\Gamma\left(\frac{m+n}{2}\right)\left(\frac{m}{n}\right)^{\frac{m}{2}}}{\Gamma\left(\frac{m}{2}\right) \Gamma\left(\frac{n}{2}\right)} y^{\frac{m}{2}-1}\left(1+\frac{m}{n} y\right)^{-\frac{m+n}{2}}$$

对于其分位点，还满足 $$F_{1-\alpha}\left(\nu_1, \nu_2\right)=\frac{1}{F_\alpha\left(\nu_2, \nu_1\right)}$$，这个性质，它的用处是，做分布表格的时候，可以假设 $\nu_1<\nu_2$，节省纸面空间。所以考试的时候如果查表查不到，那就交换分位点，交换自由度，取个倒数再去查查。

图像如下