9.13 Electrostatics
生词
| 英文 | 中文 |
|---|---|
| particle | 粒子 |
| electron | 电子 |
| proton | 质子 |
| neutron | 中子 |
| neutrally | 电中性 |
| conserved | 守恒(如电荷守恒) |
| quantise | 量子化 |
| conductor | 导体 |
| facilitate | 促进 |
| insulator | 绝缘体 |
| magnitude & direction | 大小和方向 |
| proportionality constant | 比例常数 |
| inversely related to | 成反比例关系 |
| inversely proportional | 成反比 |
| Free Space Permitivity | 自由空间介电常数 |
| repel | 排斥 |
| attract | 吸引 |
| electric field | 电场 |
| electric flux | 电通量 |
| permittivity | 介电常数 |
| potential different | 电势差 |
| perpendicular to | 垂直于 |
| symmetric | 对称的 |
| cylindrical | 圆柱形的 |
公式
库仑定律
$\Huge F = k\frac{q_1q_2}{r^2} = \frac{q_1q_2}{4\pi \varepsilon_0r^2}$
$\large k = 8.987 \times 10^9 \text{ Nm}^2\text{C}^{-2}$
$\large \varepsilon_0 = 8.854 \times 10^{-12} \text{ Fm}^{-1} \text{ 自由空间介电常数}$
电场
$\Huge \vec E = \frac{\vec F}{q}$
$\Huge E = \frac{\lambda}{2\pi\varepsilon_0r} \large\text{ 无限长的带电导线}$
$\Huge E = \frac{\sigma}{2\varepsilon_0} \large\text{ 带电平板}$
$\Huge E = \frac{U}{d}$
电通量(标量)
$\Huge E = \frac{F}{q_0} = \frac{q_0Q}{4\pi\varepsilon_0r^2}\frac{1}{q_0} = \frac{Q}{4\pi\varepsilon_0r^2}$
$\Huge \Phi = (4\pi r^2) \times \frac{Q}{4\pi\varepsilon_0r^2} = \frac{Q}{\varepsilon_0}$$\large \ \ \text{即:总电通量} = \text{面积} \times \text{场强}$
高斯定律
- 真空中,从封闭表面流出的总电通量等于封闭的电荷除以介电常数,与表面的形状无关,也与包围的电荷的排布方式无关。
- 如果知道了电通量和面积,可以计算出场强
示例:带电平板,场强与平板垂直,其中两块圆柱体的底面会对电通量产生贡献。
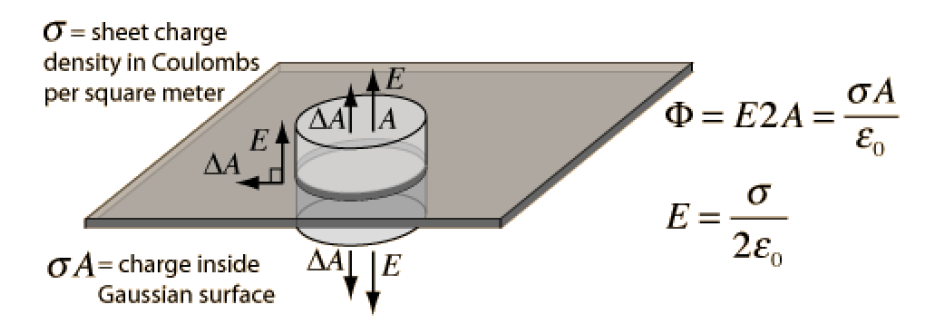
所以此时的电通量为 $\huge \Phi=E\cdot2S = \frac{S\sigma}{\varepsilon_0}$,场强大小是 $\huge E = \frac{\sigma}{2\varepsilon_0}$