4. Boolean Minimisation Using Karnaugh Maps
最小项与最大项
- 最小项:对于 n 个变量的逻辑函数而言,它的与项如果包含全部 n 个变量,即每个变量以原变量或反变量的形式出现一次且只出现一次,那么这个与项就称为该逻辑函数的最小项。
- 最大项:对于 n 个变量的逻辑函数而言,它的或项如果包含全部 n 个变量,即每个变量以原变量或反变量的形式出现一次且只出现一次,那么这个或项就称为该逻辑函数的最大项。
二者之间关系:最小项取反等于最大项,反过来也成立,即 $f(a, b, c) = \sum(0, 1, 2, 5, 7) = \Pi(3, 4, 6)$(可用德摩根定律推导)
卡诺图
卡诺图一共有 $2^n$ 个小格,每个小格子都存储一个最小项,小格之间按照格雷码排列,即保证了最小项之间逻辑相邻以及几何相邻。
其中,几何相邻包括三种:内相邻(紧挨着)、外相邻(一行或一列的两头)、中心对称
下图可以直观体现出卡诺图的几何相邻:
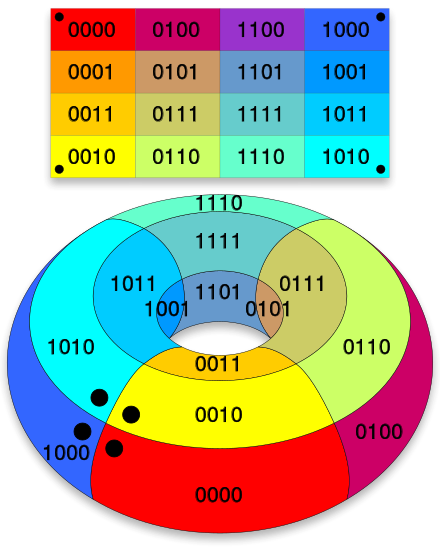
卡诺图画相邻圈时,应使每个圈包含 $2^n$ 个格子,且圈圈要尽量大。
下表是可选的卡诺图每个小格的排列样式。
| C'D' | C'D | CD | CD' | |
|---|---|---|---|---|
| A'B' | 0 | 1 | 3 | 2 |
| A'B | 4 | 5 | 7 | 6 |
| AB | 12 | 13 | 15 | 14 |
| AB' | 8 | 9 | 11 | 10 |
五变量卡诺图较为麻烦,可使用重叠画法。