Lecture 12. PSPACE-completeness PSPACE 完全性
$PSPACE = NPSPACE$!
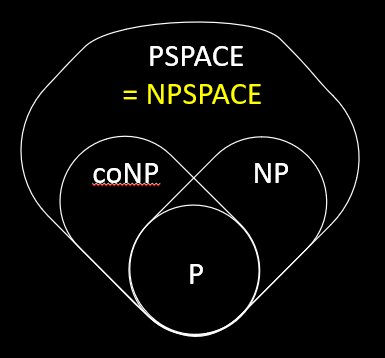
萨维奇定理 Savitch‘s Theorem
萨维奇定理指出:对于 $f(n) \geq n$,$NSPACE(f(n)) \subseteq SPACE(f^2(n))$。而由于多项式的平方还是多项式,所以 $PSPACE = NPSPACE$!
证明:证明思路与过程与证明 $LADDER_\text{DFA} \in PSPACE$ 类似。构建一个与 NTM $N$ 等价的 TM $M$,$M$ 消耗的空间是 $N$ 的平方级别:
对于 $N$ 当中的格局 $c_i, c_j$,若从 $c_i$ 在 $b$ 步骤内可以转移到格局 $c_j$,就记作 $c_i \stackrel{b}\rightarrow c_j$。
$M =$ "对于输入 $\langle c_i, c_j, b \rangle$:
- 如果 $b=1$,直接调用 $N$ 并返回 $N$ 的结果
- 如果 $b > 1$,枚举所有使用 $f(n)$ 空间的格局 $c_\text{mid}$,
- 递归的检查:$c_i \stackrel{b/2}\rightarrow c_\text{mid}$ 且 $c_\text{mid} \stackrel{b-b/2}\rightarrow c_j$
- 如果两个都接受了就接受,否则继续
- 如果全都检查了一遍都没能接受,就拒绝"
空间分析:格局的总数是 $t = |Q| \times f(n) \times d^{f(n)}$,看看 $N$ 是否能接受 $c_\text{start} \stackrel{t}\rightarrow c_\text{accept}$。由于每一层递归都需要存储一个格局,所以每一层都要消耗 $O(f(n))$ 的空间。而一共要 $\log t = O(f(n))$ 层递归,所以总空间复杂度是 $O(f^2(n))$。
PSPACE-完全性
定义:语言 $B$ 如果满足:
- $B \in PSPACE$
- $\forall A \in PSPACE$,$A \leq_p B$。
则 $B$ 是 PSPACE-完全 的。注意,定义中使用的归约是 $\leq_p$ 而不是 $\leq_{PSPACE}$,因为我们不希望让归约的过程太复杂。
通常认为的(P、NP、NP-完全、PSPACE、NPSPACE、PSPACE-完全)的关系是这样的:
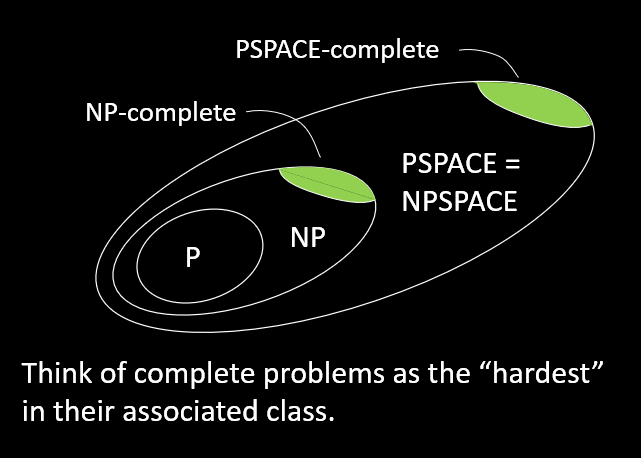
定理:$TQBF$ 是 PSPACE-完全的
没讲。不做要求。核心是 构造 规约函数。
补充:$L$ 与 $NL$
这里的 L 是 对数空间 的意思,不是线性空间的意思。
- $L = \operatorname{SPACE}(\log n)$
- $NL = \operatorname{NSPACE}(\log n)$