跳转至

Lecture 11. Introduction to Space Complexity 空间复杂性引入

定义 $f: \mathbb{N} \rightarrow \mathbb{N}, f(n) \geq n$。若图灵机 $M$ 一定停机，且对于长度为 $n$ 的输入，至多使用 $f(n)$ 个纸带的格子，那么就意味着图灵机 $M$ runs in space $f(n)$。若非确定性图灵机 $N$ 的所有分支都必定停机，且对于长度为 $n$ 的输入，每个分支都至多使用 $f(n)$ 个纸带的格子，那么 $N$ 也是 runs in space $f(n)$ 的。

定义：

  • $\operatorname{SPACE}(f(n)) = \{B \mid \text{存在确定性图灵机 } M \text{ 判定 } B \text{ 且 } M \text{ runs in space } O(f(n))\}$.
  • $\operatorname{NSPACE}(f(n)) = \{B \mid \text{存在非确定性图灵机 } N \text{ 判定 } B \text{ 且 } N \text{ runs in space } O(f(n))\}$.
  • $\operatorname{PSPACE} = \bigcup_k\operatorname{SPACE}(n^k)$.
  • $\operatorname{NPSPACE} = \bigcup_k\operatorname{NSPACE}(n^k)$.

时间复杂性强调了单带，这里空间复杂性没有。

这里空间复杂性并不是指的额外空间占用，而是总共的空间占用。那么问题来了，$L$ 等亚线性是什么情况？亚线性空间的都是使用两个纸带的模型。一个纸带是输入的，只读；另一个纸带随便。

时空复杂性的关系

定理：对于所有的 $t(n) \geq n$，都有 $\operatorname{TIME}(t(n)) \subseteq \operatorname{SPACE}(t(n)) \subseteq \operatorname{TIME}(2^{O(t(n))}) = \bigcup_c \operatorname{TIME}(c^{t(n)})$。

证明：runs in $t(n)$ steps 的图灵机，不可能使用超过 $t(n)$ 个纸带格子。反之，能使用 $t(n)$ 个纸带格子的图灵机，至少需要运行 $t(n)$ 步，但也不能消耗超过 $c^{t(n)}$ 的时间（假设不死循环，$c$ 代表格局的数量）

推论：$P \subseteq PSPACE$。但是注意 $NSPACE$ 的不一定在 $P$ 中。

定理：$NP \subseteq PSPACE$。但是注意 $NSPACE$ 的不一定在 $NP$ 中。

证明：只需先证明出：

  1. $SAT \in PSPACE$。
  2. 归约，若 $A \leq_p B$ 且 $B \in PSPACE$，那么就能推出 $A \in PSPACE$

定义：$coNP = \{\overline{A} \mid A \in NP\}$。$\overline{HAMPATH} \in coNP$。

$TAUTOLOGY = \{\langle \phi \rangle \mid \text{任意赋值都可以让 } \phi \text{ 真}\}$，$TAUTOLOGY \in coNP$。

$coNP \subseteq PSPACE$。

但是目前学术界不知道，是否 $P = PSPACE$，或者是否 $P = NP = coNP = PSPACE$。

通常认为的关系是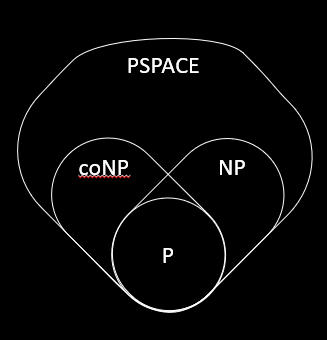：image-20221205111403262

事实上，以后还将指出：$PSPACE = NPSPACE$。

TQBF 问题

量词（quantifier） 包括 $\exists$ 和 $\forall$。

定义 quantified Boolean formula（QBF）表示开头具有 $\exists$ 或 $\forall$ 修饰的布尔式子。所有布尔变量都在作用域 scope 内。有的 QBF 是真的，有的是假的。

  • $\phi_1=\forall x \exists y[(x \vee y) \wedge(\bar{x} \vee \bar{y})]$ 真
  • $\phi_2=\exists y \forall x[(x \vee y) \wedge(\bar{x} \vee \bar{y})]$ 假

定义问题 $TQBF = \{\langle \phi \rangle \mid \phi \text{ 是一个真的 QBF}\}$。根据定义，刚刚两个式子：

  • $\phi_1 \in TQBF$
  • $\phi_2 \not\in TQBF$

不难发现，$SAT$ 问题就是仅含有 $\exists$ 的 $TQBF$ 问题。

定理：$TQBF \in PSPACE$。

证明：设计一个图灵机 $M$。$M =$ "On input $\langle \phi \rangle$:

  1. 若 $\phi$ 不具有量词，那么 $\phi$ 就不含变量。所以 $\phi$ 的形式就是 $\phi = 1$ 或 $\phi = 0$。直接输出
  2. 若形式是 $\phi = \exists x \psi$，那么分别令 $x=1$ 和 $x=0$，递归地计算 $\psi$。若任意一个计算接受了，就接受。否则就拒绝。
  3. 若形式是 $\phi = \forall x \psi$，那么分别令 $x=1$ 和 $x=0$，递归地计算 $\psi$。若两个计算都接受了，就接受。否则就拒绝。"

接下来分析这个的空间占用。

每一层的递归，都要消耗常数级别的空间来记录 $x$ 的值。而递归的深度，不会超过量词的个数，于是也就不会超过 $n = |\langle \phi \rangle |$。故，$TQBF \in \operatorname{SPACE}(n) \subseteq PSPACE$。

Ladder 问题

ladder 是指，一堆由长度相等的字符串（而不是字符）构成的数组（序列），且每一个相邻的字符串，仅有一个字符不同。（有点像格雷码呢）

比如，这个 WORK 到 PLAY 的序列就是一个 ladder：

image-20221205115425843

A word ladder for English is a ladded of English words.

Let $A$ be a language, a ladder in $A$ is a ladder of strings in $A$.

定义：$LADDER_\text{DFA} = \{\langle B, u, v \rangle \mid B \text{ 是 DFA，且 } L(B) \text{ 包含一个 ladder } y_1, y_2, \cdots, y_k \text{ 且满足 } u = y_1, v = y_k\}$ 。

定理：$LADDER_\text{DFA} \in NPSPACE$

证明思路比较简单：（注意图灵机无法存储序列，且必须停机）。

该非确定性图灵机 $N =$ "对于输入 $\langle B, u, v \rangle$:

  1. 若 $|u| \not= |v|$ 直接拒绝
  2. 令 $y=u$，令 $m = |u|$
  3. 重复以下步骤至多 $t = |\Sigma|^m$ 次：
    1. 非确定性的修改 $y$ 当中的一个符号
    2. 若修改后的 $y \not \in L(B)$ 则直接拒绝
    3. 若修改后的 $y = v$ 则接受
  4. 如果已经运行了 $t$ 步还没有接受，那么也拒绝。"

这台图灵机虽然步骤 3 消耗的时间达到了指数级别，但是它的额外空间占用始终是线性级别（存储当前串串 $y$ 和运行上限次数 $t$）的。故 $LADDER_\text{DFA} \in PSPACE$.

定理：$LADDER_\text{DFA} \in \operatorname{SPACE}(n^2) \subset PSPACE$

考虑一个简化的问题：$BOUNDED-LADDER_\text{DFA} = \{\langle B, u, v, b \rangle \mid B \text{ 是一台 DFA 且 } L(B) \text{ 中 } u \stackrel{b}\rightarrow v\}$。

构造图灵机：$B-L =$ "对于输入 $\langle B, u, v, b \rangle$，

  1. 令 $m = |u| = |v|$
  2. 对于 $b=1$ 的情况，若 $u, v \in L(B)$ 且 $u, v$ 的编辑距离在 $1$ 以内，则接受，否则决绝
  3. 对于 $b > 1$ 的情况，对于每个 $L(B)$ 中长度为 $|u|$ 的串串 $w$，重复以下步骤（枚举语言中所有指定长度的串串）：
    1. 递归地检查：是否能 $u \stackrel{b/2}\rightarrow w$ 且 $w \stackrel{b - b/2}\rightarrow v$（二分）
    2. 若两边的调用都接受了，就接受，否则继续
  4. 拒绝（所有检查都失败了）"

那么，对于 $\langle B, u, v \rangle \in LADDER_\text{DFA}$ 的判定，就可以转化为 $\langle B, u, v, t \rangle \in BOUNDED-LADDER_\text{DFA}$，其中 $t = |\Sigma|^m$。

空间分析：每一层消耗 $O(n)$ 的空间来记录单词（选择的 $w$ 是谁），递归总共 $\log t = O(n)$ 层，故空间复杂度是 $O(n^2)$。