Lecture 7. Reducibility 可归约性
简单地说,归约(reduction)就是把一个问题转化成另一个问题,且可以用第二个问题的解来解第一个问题。
如果有 A 和 B 两个语言(或问题),如果可以用 B 来解决 A,就说 A 可归约到 B。
- 如果 B 容易解决,那么 A 也会容易解决。因为 A 可以转化到 B 去。
- 但如果 A 比较难,B 也会难。 因为如果 B 不难,A 也不会难的。我们着重应用第二条。
例如:
- 求矩形的面积,可以归约到求长宽
- $A_\text{NFA}$ 可归约到 $A_\text{DFA}$
- $HALT_\text{TM}$ 可归约到 $A_\text{TM}$
当然,有可能会存在 A 和 B,使 A 能归约到 B,同时 B 也能归约到 A,即 AB 等价。
语言理论中的不可判定问题
比如,对于语言 $A_\text{TM}$ 是否可判定,可以归约到另一个语言 $HALT_\text{TM} = \{\langle M, w \rangle \mid \text{图灵机 } M \text{ 在输入 } w \text{ 上会停机} \}$ 是否可判定。这是停机问题(halting problem)。
定理:$HALT_\text{TM}$ 不可判定。证明思路是采用反证法(事实上,大部分的不可判定,都可以用归约到 $A_\text{TM}$ 的方法证明)。
假设 $HALT_\text{TM}$ 可判定,就能证明 $A_\text{TM}$ 可判定(设 $R$ 是 $HALT_\text{TM}$ 的判定器,构造图灵机 $S$ 判定 $A_\text{TM}$):
$S =$ “在输入 $\langle M, w \rangle$ 上,
- 先跑一遍判定器 $R$ 看看 $M$ 是否对于输入 $w$ 停机。如果不能停机,直接拒绝。
- 由于现在确保 $M$ 可以停机,于是就直接模拟运行 $M$,直到停机为止。若 $M$ 接受则 $S$ 接受,$M$ 拒绝则 $S$ 拒绝”
但是这与事实不符,因为 $A_\text{TM}$ 明明是不可判定的,这里证明出它可判定,产生了矛盾,所以最初的假设不成立。于是 $HALT_\text{TM}$ 不可判定。
定理:$E_\text{TM}$ 不可判定。 像刚才一样,用反证法(归约)。
先假设 $E_\text{TM}$ 可判定,就能证明 $A_\text{TM}$ 可判定(设 $R$ 是 $E_\text{TM}$ 的判定器,构造图灵机 $S$ 判定 $A_\text{TM}$)。
$S =$ “在输入 $\langle M, w \rangle$ 上
- 第一步,把图灵机 $M$ 转化成一个新的图灵机 $M_w$,其中 $M_w =$ ‘在输入 $x$ 上:
- 如果 $x \not= w$ 则直接拒绝,否则在 $M$ 上面运行 $w$。
- 若 $M$ 接受,$M_w$ 接受,否则拒绝。’
- 可以看到,$M_w$ 和 $M$ 非常像,唯一的差别就是提前检查了一下是否 $x \not= w$。所以,$L(M_w) = \begin{cases}{w} & M \text{ 接受 } w \\ \emptyset & M \text{ 拒绝 } w \end{cases}$。
- 第二步,用 $R$ 检查 $L(M_w)$是否是空的,即是否满足 $L(M_w) = \emptyset$,也就是在输入 $\langle M_w \rangle$ 上运行 $R$ 看是否接受。如果是,意味着 $M$ 拒绝 $w$,则拒绝。否则意味着 $M$ 接受 $w$,则接受。”
但是这与事实不符,因为 $A_\text{TM}$ 明明是不可判定的,所以 $S$ 不可能知道 $M$ 能否接受 $w$。这里证明出它可判定,产生了矛盾,所以最初的假设不成立。于是 $E_\text{TM}$ 不可判定。
映射可归约性 Mapping Reducibility
也有的教材,写作 多一可归约性(many-one reducibility)。
图灵机计算函数的方法是,把函数的输入放在纸带上,开始运行,最终停机,把停机后纸带上的内容作为函数的输出。
定义:如果有一个图灵机 $F$,使得在在每个输入 $w$ 上都停机,且此时只有 $f(w)$ 出现在纸带上,则称函数 $f:\Sigma^* \rightarrow \Sigma^*$ 是一个 可计算函数(computable function)。
定义:如果存在一个可计算函数 $f:\Sigma^* \rightarrow \Sigma^*$ 使得对于每个 $w$,$w \in A \Leftrightarrow f(w) \in B$,记作 $A \leq_m B$,则称函数 $f$ 是 $A$ 到 $B$ 的 归约,语言 $A$ 是 映射可归约(mapping reducible) 到语言 $B$ 的。注意,定义当中的符号 $\Leftrightarrow$ 的含义是 当且仅当。也就是,如果有 $w \not \in A$,则也必须满足 $f(w) \not \in B$。
也就是说,如果要证明映射可归约性,只需要把这个可计算的归约函数 $f$ 写出来就好了。$f$ 的定义域永远是 $A$,到达域永远是 $B$。注意要满足当且仅当的特性才能是可计算函数。
下图可以形象化的表达可计算函数的定义:
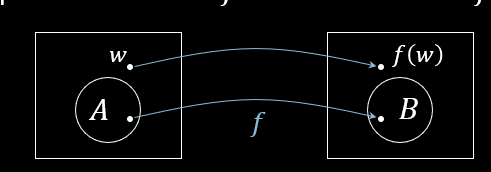
举一个映射规约的例子:$A_\text{TM} \leq_m \overline{E_\text{TM}}$,对应的可计算的规约函数 $f$ 是:$f(\langle M, w \rangle) = \langle M_w \rangle$。因为 $\langle M, w \rangle \in A_\text{TM} \Leftrightarrow \langle M_w \rangle \in \overline{E_\text{TM}}$,即:$M$ 接受 $w$ 当且仅当 $L(M_w) \not= \emptyset$。~~课件上写成了 $L(\langle M_w \rangle) \not= \emptyset$,应该是课件错了吧,反正书上是没有那左右 angle 符号的。~~
根据定义,如果 $A \leq_m B$,那么 $\overline A \leq_m \overline B$ 同时成立。 不过,$B \leq_m A$ 不一定成立,要不然干嘛要用小于号而不是等于号来表示映射可归约呢?
不仅如此,$\leq_m$ 是一个可传递的二元关系。也就是说,如果 $A \leq_m B$ 且 $B \leq_m C$ 同时成立,就能够得到 $A \leq_m C$.
关于可判定性
定理:若 $A \leq _mB$ 且 $B$ 是可判定的,则 $A$ 也是可判定的。证明:设图灵机 $R$ 判定 $B$,构造 $A$ 的判定器 $S$:“在输入 $w$ 上,首先计算 $f(w)$,然后用 $f(w)$ 的值作为 $R$ 的输入,检查是否满足 $f(w) \in B$,最终 $R$ 接受就接受,否则拒绝。”
推论:若 $A \leq_m B$ 且 $A$ 是不可判定的,则 $B$ 也是不可判定的。
定理:若 $A \leq_m B$ 且 $B$ 是图灵可识别的,则 $A$ 也是图灵可识别的。证明方法与刚才类似。
推论:若 $A \leq_m B$ 且 $A$ 不是图灵可识别的,则 $B$ 也不是图灵可识别的。这一条推论对于证明图灵不可识别尤其重要。
注意:上述关于图灵可识别性的定理和推论,只适用于映射归约,而对于普通的归约,是不满足的。举个例子:$\overline{A_\text{TM}}$ 可归约到它的补 $A_\text{TM}$。后者是图灵可识别的,但是前者不是。
映射可归约性和普通可归约性对比
- 映射可归约性:把 A 问题转化成 B 问题。是一种特殊的可归约性问题,对于证明图灵不可识别非常好用。
- 普通可归约性:用 B 问题来解决 A 问题。在概念上更加简单,对于证明不可判定非常好用。
注意:
- $A$ 可归约到 $\overline A$
- 但是 $A$ 可能并不能映射归约到 $\overline A$,比如 $\overline{A_\text{TM}} \not\leq_m A_\text{TM}$(图灵可识别语言在补运算下不封闭)
证明不可判定、图灵不可识别的技巧
如果要证明 $B$ 不可判定,一般做法是找到一个已知的可归约到 $B$ 的不可判定语言 $A$(通常选择 $A_\text{TM}$),然后假设 $B$ 可判定,令 $R$ 是 $B$ 的判定器,然后构造出一个图灵机 $S$ 判定 $A$。然而 $A$ 是不可判定的,产生矛盾,假设不成立,于是 $B$ 不可判定。
如果要证明 $B$ 图灵不可识别,一般做法是,找到一个已知的映射可归约到 $B$ 的图灵不可识别的语言 $A$(通常选择 $\overline{A_\text{TM}}$),然后写出规约函数 $f$。(上面第二条推论)
例:证明 $REGULAR_\text{TM} = \{\langle M \rangle \mid M \text{ 是图灵机且 } L(M) \text{ 是正则语言}\}$ 不可判定
廖智炫教我的。核心思路是:
假设 $R$ 是 $REGULAR_\text{TM}$ 的判定器。用 $R$ 构造一个图灵机 $S$。
先搞一个 $M_2$ 出来,$M$ 接受 $w$ 的时候,$M_2$ 接受正则语言 $\Sigma^$;$M$ 拒绝 $w$ 的时候 $M_2$ 只接受一个非正则语言 $0^n1^n$。换句话说,$M_2$ 接受所有具有 $0^n1^n$ 形式的串串,且在 $M$ 接受 $w$ 的时候接受任意串($\Sigma^$)。
然后 $S$ 把 $\langle M_2 \rangle$ 作为输入调用 $R$。如果 $R$ 接受 $S$ 就接受,$R$ 拒绝 $S$ 就拒绝。
于是这个 $S$ 具有了判定 $A_\text{TM}$ 的作用。
例:证明 $E_\text{TM}$ 是图灵不可识别的
上面已经指出过:$A_\text{TM} \leq_m \overline{E_\text{TM}}$。所以把不等号两边分别取反,仍然成立:$\overline{A_\text{TM}} \leq_m E_\text{TM}$。对应的规约函数仍然是:$f(\langle M, w \rangle) = \langle M_w \rangle$。因为 $\langle M, w \rangle \in \overline{A_\text{TM}} \Leftrightarrow \langle M_w \rangle \in E_\text{TM}$,即:$M$ 拒绝 $w$ 当且仅当 $L(M_w) = \emptyset$。
于是,$E_\text{TM}$ 既不可判定(之前证明过),也不可识别(现在刚证明)。
例:证明 $EQ_\text{TM}$ 既不是图灵可识别的,也不是补图灵可识别的
即:$EQ_\text{TM}$ 和 $\overline{EQ_\text{TM}}$ 都不是图灵可识别的。
要证明这个论题,只需分别证明:
- $\overline{A_\text{TM}} \leq_m EQ_\text{TM}$,即证明不是图灵可识别的
- $\overline{A_\text{TM}} \leq_m \overline{EQ_\text{TM}}$,即证明不是补图灵可识别的
最后再应用上面第二条推论:若 $A \leq_m B$ 且 $A$ 不是图灵可识别的,则 $B$ 也不是图灵可识别的。就能证明完了。
回忆一下:$A_\text{TM}$ 及其补的格式是 $\langle M,w \rangle$,$EQ_\text{TM}$ 及其补的格式是 $\langle T1, T2 \rangle$。
证明方法是,对于任意的字符串 $w$,都构建对应的图灵机 $T_w$,
$T_w =$“对于输入 $x$, 1. 忽略 $x$ 2. 在 $M$ 上面执行 $w$”
也就是说,不管 $T_w$ 遇到什么样的输入,都不管他,直接用 $M$ 执行 $w$。
另外,再构建一个图灵机 $T_\text{reject}$,不管遇到啥输入都是直接拒绝。还有一个 $T_\text{accept}$,不管遇到啥输入都直接接受。
那么:
- 对于前者 $\overline{A_\text{TM}} \leq_m EQ_\text{TM}$,可以构建出归约函数 $f(\langle M,w \rangle) = \langle T_w, T_\text{reject} \rangle$,因为 $M$ 不接受 $w$(形式化表述为 $\langle M,w \rangle \in \overline{A_\text{TM}}$),当且仅当 $M$ 总是拒绝 $w$(形式化表述为 $T_w = T_\text{reject}$,即 $\langle T_w, T_\text{reject} \rangle \in EQ_\text{TM}$)。
- 对于后者 $\overline{A_\text{TM}} \leq_m \overline{EQ_\text{TM}}$,可以构建出归约函数 $f(\langle M,w \rangle) = \langle T_w, T_\text{accept} \rangle$,因为 $M$ 不接受 $w$(形式化表述为 $\langle M,w \rangle \in \overline{A_\text{TM}}$),当且仅当 $M$ 总是不接受 $w$(形式化表述为 $T_w \not= T_\text{accept}$,即 $\langle T_w, T_\text{accept} \in \overline{EQ_\text{TM}}$)。~~虽然很是拗口,但要努力理解一下~~
两个归约函数都写出来了,于是这个论题也证明完了。
计算历史方法 Computation History Method
希尔伯特第十题
语言 $D = \{\langle p \rangle \mid \text{多项式 }p(x_1,x_2, \cdots, c_k) = 0 \text{ 具有整数根}\}$。该语言不可判定。
证明思路 1:证明 $A_\text{TM}$ 可归约到 $D$。由于 $A_\text{TM}$ 不可判定,所以 $D$ 也不可判定。
但是很难证明这个可归约性。这里需要使用 计算历史方法(computation history method)。
波斯特对应问题 Post Correspondence Problem
以骨牌簇的形式给出若干对字符串:$P=\left\{\left[\begin{array}{c}t_1 \\ b_1\end{array}\right],\left[\begin{array}{c}t_2 \\ b_2\end{array}\right], \ldots,\left[\begin{array}{c}t_k \\ b_k\end{array}\right]\right\}$。
定义 匹配 是指一个有限的序列(可重复)$\left[\begin{array}{c}t_{i_1} \\ b_{i_1}\end{array}\right]\left[\begin{array}{c}t_{i_2} \\ b_{i_2}\end{array}\right] \quad \cdots\left[\begin{array}{c}t_{i_l} \\ b_{i_l}\end{array}\right]$,使得 $t_{i_1} t_{i_2} \cdots t_{i_l}=b_{i_1} b_{i_2} \cdots b_{i_l}$。
如:$P=\left\{\left[\begin{array}{c}a b \\ a b a\end{array}\right],\left[\begin{array}{c}a a \\ a b a\end{array}\right],\left[\begin{array}{c}b a \\ a a\end{array}\right],\left[\begin{array}{c}a b a b \\ b\end{array}\right]\right\}$,于是可重复排列 $1,2,3,2,4$ 就是 $P$ 的一个匹配(使 $s=t=abaabaaaabab$)。通俗的说,就是把骨牌簇可重复地重新排列,如果上半部分和下半部分相等,这个排列就称之为匹配。
波斯特对应问题,指的就是:给定骨牌簇 $P$,问 $P$ 是否拥有匹配?
令语言 $PCP = \{\langle P \rangle \mid \text{骨牌簇 } P \text{ 具有匹配}\}$。该语言是不可判定的。要证明这个东西,也需要 计算历史方法。
回顾:图灵机的格局
图灵机的格局是一个三元组 $(q,p,t)$,$q$ 表示状态,$p$ 表示读写头的位置,$t$ 表示纸带的内容。
一个格局可以被编码用字符串表示为 $t_1qt_2$,其中 $t=t_1t_2$,且读写头的位置在 $t_2$ 的第一个符号上。如:格局 $q_3, 6, aaaaaabbbbb$ 可以编码为 $aaaaaq_3abbbbb$。
格局可以代表图灵机在一个时刻的快照,就像电子游戏里面的存档一样。
计算历史
定义:图灵机 $M$ 在输入 $w$ 上的一个 接受计算历史(accepting computation history) 是指一个格局序列 $C_1, C_2, \cdots, C_\text{accept}$,其中 $C_1$ 是起始格局。类似地,可以定义 拒绝计算历史(rejecting computation history)。注意,计算历史是一段格局的 序列,而不是一个单独的格局。
计算历史可以被编码为 $C_1 \# C_2 \# \cdots \# C_\text{accept}$ 的形式(当然,每一个 $C_i$ 也被编码了)。比如下面这一坨就是一个接受计算历史。
$\overbrace{q_0 w_1 w_2 \cdots w_n}^{C_1} \# \overbrace{a q_7 w_2 \cdots w_n}^{C_2} \# \overbrace{a c q_8 w_3 \cdots w_n}^{C_3} \# \quad \cdots \quad \# \overbrace{\cdots q_{\text {accept }} \cdots}^{C_{\text {accept }}}$
线性界限自动机 Linearly Bounded Automata
是一种特殊的受到限制的图灵机,读写头不能移动到输入串以外的区域,也就是纸带的长度等于输入串的长度。
定义语言 $A_\text{LBA} = \{\langle B,w \rangle \mid \text{LBA } B \text{ 接受 } w\}$。虽然 LBA 也是一种图灵机,但是 其实 $A_\text{LBA}$ 是可判定的!因为,假如输入串的长度是 $n$,那么 LBA 的格局数最多就是 $|Q| \times n \times |\Gamma|^n$。因此,如果一台 LBA 运行足够久还不停机,仅有一种可能,就是进入了一个曾经经历过的格局。那么就可以构造出 $A_\text{LBA}$ 的判定器了。$D_{A-LBA} =$ “在输入 $\langle B, w \rangle$ 上,在 LBA $B$ 上运行 $w$ $|Q| \times |w| \times |\Gamma|^{|w|}$ 步,如果接受了就接受,如果拒绝了或者没停机,就拒绝。”
然而,$E_\text{LBA} = \{\langle B \rangle \mid B \text{ 是 LBA 且 } L(B) = \emptyset\}$ 是不可判定的。证明思路是证明 $A_\text{TM}$ 可归约到 $E_\text{LBA}$。
跟之前的思路一样,假设判定器 $R$ 判定 $E_\text{LBA}$,那么就可以构造出一个判定器 $S$ 判定 $A_\text{TM}$。
$S =$ “在输入 $\langle M, w \rangle$ 上,
- 构造一个 LBA $B_{M,w}$,这个 LBA 的输入是 $x$,它判断 $x$ 是否是 $M$ 在 $w$ 上的一个接受计算历史。也就是说,只有输入的 $x$ 是 $M$ 在 $w$ 上的一个接受计算历史,才接受。所以,$L(B_{M,w})$ 包含了 $M$ 在 $w$ 上的所有的接受计算历史。
- 然后,用 $R$ 来判断 $L(B_{M,w})$ 是否是 $\emptyset$。如果不是空集,意味着存在接受计算历史,也就意味着图灵机 $M$ 最终接受 $w$,所以 $\langle M,w \rangle \in A_\text{TM}$,那么 $A_\text{TM}$ 的判定器 $S$ 就接受,否则 $S$ 拒绝。”
接下来考虑 LBA $B_{M,w}$ 怎么构造。
$B_{M,w} =$ “在输入 $x$ 上(注意 $x$ 的形式是一个计算历史的编码),
- 检查 $x$ 是否是 $C_1\#$ 开头的($C_1$ 是 $M$ 在 $w$ 上的起始格局)
- 再检查是否每一个 $C_{i+1}$ 都能合法的从 $C_i$ 转移过来
- 然后再检查最后一个格局是否是接受格局。
- 如果三项检查都通过了,意味着输入的 $x$ 是一个接受计算历史,那么 $B_{M,w}$ 就接受。如果任意一项检查没有通过,就拒绝。”
波斯特对应问题 Post Correspondence Problem
令语言 $PCP = \{\langle P \rangle \mid \text{骨牌簇 } P \text{ 具有匹配}\}$。接下来证明 语言 $PCP$ 是不可判定的。
证明 $A_\text{TM}$ 可归约到 $PCP$。利用计算历史方法(很像是归约法)。
先考虑简单情况,即匹配必须以 $\left[\begin{array}{l}t_1 \\ b_1\end{array}\right]$ 开头。
假设图灵机 $R$ 判定 $PCP$,那么就能够用 $R$ 造出一个图灵机 $S$ 判定 $A_\text{TM}$。
$S =$ “在输入 $\langle M, w \rangle$ 上,
- 构造一个 PCP 的实例 $P_{M,w}$ 使得匹配都是 $M$ 在 $w$ 上的接受计算历史(稍后说明如何构造 $P_{M,w}$)。
- 然后用 $R$ 来判定 $P_{M,w}$ 是否拥有匹配。如果有匹配,说明 $M$ 在 $w$ 上有接受计算历史,意味着 $M$ 最终会接受 $w$。若 $R$ 接受, $S$ 就接受,否则 $S$ 就拒绝。”
于是,$S$ 就可以判定 $A_\text{TM}$,但这不可能,假设不成立,故 $PCP$ 不可判定。
接下来描述如何构造出 $P_{M,w}$。考虑起始骨牌 $\left[\begin{array}{l}u_1 \\ v_1\end{array}\right]=\left[\begin{array}{l}\# \\ \# q_0 w_1 \cdots w_n \#\end{array}\right]$,
~~关于如何构造 $P_{M,w}$ 一直都还没学明白。。。~~
虽然说 $PCP$ 不可判定,但是 $PCP$ 图灵可识别。因为可以不停的尝试各种的可能的匹配(可能会耗时无限久)。于是可以根据「一个语言可判定,当且仅当既是图灵可识别又是补图灵可识别的」得到一个没啥用的推论:$PCP$ 不是补图灵可识别的。
$ALL_\text{CFG}$ 不可判定
张老师说其实跟证明 PCP 的不可判定性一模一样的。待补充。
语言问题可判定性总结
| DFA | CFG | LBA | TM | |
|---|---|---|---|---|
| 接受性 A | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{red}\text{✗}$ |
| 空性 E | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{red}\text{✗}$ | $\color{red}\text{✗}$ |
| 等价性 EQ | $\color{green}\checkmark$ | $\color{red}\text{✗}$ | $\color{red}\text{✗}$ | |
| 满性 ALL | $\color{red}\text{✗}$ | |||
| 停机性 HALT | $\color{green}\checkmark$ | $\color{red}\text{✗}$ | ||
| 正则性 REGULAR | $\color{red}\text{✗}$ |
常见形式语言分类
(都不属于更低一层)
| 语言类 | 语言示例 |
|---|---|
| 非图灵可识别 | $\overline{A_\text{TM}}$,$EQ_\text{CFG}$,$EQ_\text{TM}$,$\overline{EQ_\text{TM}}$ |
| 图灵可识别 | $A_\text{TM}$,$HALT_\text{TM}$,$PCP$,$\overline{EQ_\text{CFG}}$ |
| 可判定 | $A_\text{LBA}$,$E_\text{CFG}$,$EQ_\text{DFA}$ |
| 上下文有关 | $0^n1^n2^n$,$ww$,接受计算历史 |
| 上下文无关 | $0^n1^n$,$ww^\mathcal{R}$,非 $ww^\mathcal{R}$,非 $ww$,非接受计算历史 |
| 正则 | $0^*1^*$ |
语言类封闭性总结
| 补 | 交 | 并 | 连接 | 星号 | |
|---|---|---|---|---|---|
| 图灵可识别(TM) | $\color{red}\text{✗}$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ |
| 可判定(TM) | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ |
| 上下文有关(LBA) | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ |
| 上下文无关(PDA) | $\color{red}\text{✗}$ | $\color{red}\text{✗}$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ |
| 正则(DFA) | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ | $\color{green}\checkmark$ |