Lecture 6. Undecidability 不可判定性

函数知识回顾（CS172 笔记摘录）

函数的定义域，值域，像，到达域（domain，range，image，codomain）

定义域：略
值域：略
像：是值域的一个子集，这个子集包含由函数 $f$ 映射来的一些元素。注意像并不是函数的值。函数的值是值域当中的某个元素，而函数的像是至于当中的某个子集。
到达域，又称对应域，与值域不同。值域是到达域的一个子集。满射函数的值域与到达域是相等的。

函数的单射，满射，双射（injective，surjective，bijective）

单射，是指，像中的每一个元素，都是由定义域中唯一的一个元素映射来的：$(\forall x, y \cdot(x \in X \wedge y \in X \wedge f(x)=f(y)) \rightarrow(x=y))$
满射，是指，像中的每一个元素，都能被定义域中的元素映射得到：$(\forall z \cdot z \in Y \rightarrow(\exists x \cdot x \in X \wedge f(x)=z))$
双射，是指，既是单射，又是满射。即双射的两个集合，元素个数一定相等。
在 CS355FZ 当中，有时候说 单射是 one to one，满射是 onto，双射 correspondence。

偏函数（partial function）

大概就是，定义域当中有的元素没有映射出去。

如果进一步限制约束偏函数的定义域，那么就会变成 total function（翻译过来可能是全函数）

比如，阶乘函数 $\texttt{fact(x)}$ 的定义域如果是整数集，那么它就是一个偏函数，因为 $\texttt{fact(-1)}$ 不知道。

无限集的大小

定义：当集合 $A$ 和集合 $B$ 之间存在一个双射关系 $f:A \rightarrow B$，则称集合 $A$ 和集合 $B$ 具有相同规模（same size）。非形式化的讲，就是可以将两个集合当中的元素两两配对。

自然数集 $\mathbb{N} = \{ 1, 2, 3, \cdots \}$，整数集 $\mathbb{Z} = \{\cdots, -2, -1, 0, 1, 2, \cdots\}$。这两个集合之间存在双射，因为存在函数：

$$f(x)= \begin{cases}-2x+1, & \text { if } x \leq 0 \ 2x, & \text { if } x>0\end{cases}$$

定义：与自然数集 $\mathbb{N}$ 之间存在双射关系的函数，以及所有的有限集，称为可数集。所以整数集 $\mathbb{Z}$ 是 可数（countable） 的。

更大的无限集？（摘自 CS172 笔记）

注意 CS172 当中的集合 $\mathbb{N}$ 是包含 $0$ 的，不过影响不大。

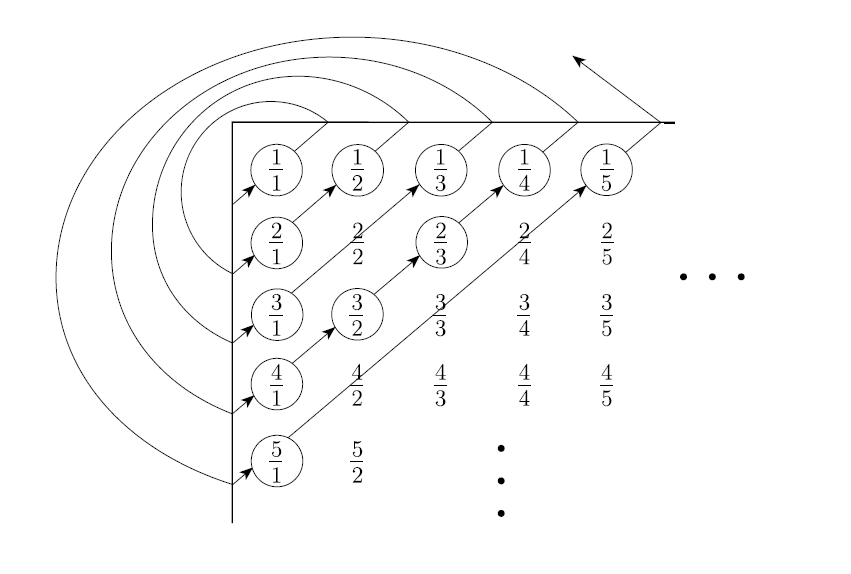
考虑集合 $\mathbb{N} \times \mathbb{N}$。 $$ \begin{array}{ccccc} (0,0) & (1,0) & (2,0) & (3,0) & \cdots \\ (0,1) & (1,1) & (2,1) & (3,1) & \cdots \\ (0,2) & (1,2) & (2,2) & (3,2) & \cdots \\ (0,3) & (1,3) & (2,3) & (3,3) & \cdots \\ \vdots & \vdots & \vdots & \vdots \end{array} $$

这个集合，铺成正方形，每一行每一列都是无限个…但是如果从左上角开始，斜着计数，就可以列出这种形式：$\{(0,0),(1,0),(0,1),(0,2),(1,1),(2,0),(3,0),(2,1),(1,2),(0,3), \ldots\}$…看起来依然是可以数出来的吼

那么如何计算这个集合 $\mathbb{N} \times \mathbb{N}$ 的势？

不妨定义函数 $f((i,j)) = 2^i \times 3^j$。由于 $2$ 和 $3$ 都是质数，由唯一分解定理得知，$f$ 是双射的，即每个 $(i,j)$ 都能通过 $f$ 映射到某个整数，而那个整数也只能分解成 $2^i\times 3^j$ 的形式。于是，$\mathbb{N} \times \mathbb{N}$ 就与 $\mathbb{N}$ 的一个无限子集建立了双射关系。而 $\mathbb{N}$ 的无限子集的势也是 $\aleph_0$。故，$\mathbb{N} \times \mathbb{N}$ 的势还是 $\aleph_0$，这个集合是可数集。

扩展一步，如果是 $\mathbb{N} \times \mathbb{N} \times \mathbb{N}$，甚至是更多维数，依然是可数的。二维的，用前两个质数，三维的就用前三个，$k$ 维的就用前 $k$ 个质数，就好了。比如，$(3,4,2,0,2,1)$ 就可以映射到 $2^3 \times 3^4 \times 5^2 \times 7^0 \times 11^2 \times 13^1$。

再拓展一下，对于有理数集 $\mathbb{Q}$ 以及正有理数集 $\mathbb{Q}^+ = \{\frac{n}{m} \mid n, m \in \mathbb{N}\}$，也都是可数集。因为有理数 $\frac{p}{q}$ 可以与 $(p,q)$ 双射，这就回到了刚才的二维问题。

对角化方法

CS355 的课本当中，给出了另一种证明集合 $\mathbb{N} \times \mathbb{N}$ 可数的方法：从左上角开始，画一条斜着的线，不断地把这条线往右下方移动。每次碰到线的数字，都加入集合当中（忽略约分后已存在的数字）。这样，每划到一个有理数，就增加一个计数器，而计数器的值是整数，所以正有理数集也是可数的。

注意英文单词对角线：diagonal。如果考试考了，要记得拼写。

事实上可以把这种对角化方法想象成二维坐标系。分子分母分别是横纵坐标。

然而，实数集 $\mathbb{R}$ 不是可数集。

用对角化方法证明：$\mathbb{R}$ 不可数

首先假设 $\mathbb{R}$ 可数，那么就一定存在一个 $f:\mathbb{N} \rightarrow \mathbb{R}$ 的双射关系。

假设 $f$ 的前几项如下表：

$$\begin{array}{c|c} n & f(n) \\ \hline 1 & 2.\textbf{7}18281828 \ldots \\ 2 & 3.1\textbf{4}1592653 \ldots \\ 3 & 0.00\textbf{0}000000 \ldots \\ 4 & 1.414\textbf{2}13562 \ldots \\ 5 & 0.1428\textbf{5}7242 \ldots \\ 6 & 0.20787\textbf{9}576 \ldots \\ 7 & 1.234567\textbf{8}90 \ldots \\ \vdots & \vdots \end{array}$$

只要我能够找到一个实数 $x$ 一定不在这个 $f$ 的表格里面，就能够证明 $\mathbb{R}$ 不可数了。这个 $x$ 很好找。

对于 $f(1)$，小数点后第 $1$ 位数字是 $7$，那我就令 $x$ 的小数点后第 $1$ 位数字不是 $7$
对于 $f(2)$，小数点后第 $2$ 位数字是 $4$，那我就令 $x$ 的小数点后第 $2$ 位数字不是 $4$
对于 $f(3)$，小数点后第 $3$ 位数字是 $0$，那我就令 $x$ 的小数点后第 $3$ 位数字不是 $0$
…
那么，对于 $f(n)$，不管 $n$ 取值是多少，我都让 $x$ 的第 $n$ 位与 $f(n)$ 不同，那么这个 $x$ 就一定不会在这个表格里面。所以，这个 $x$ 无法与 $\mathbb{N}$ 的某个元素双射。于是，$\mathbb{R}$ 不可数。

推论

令 $\mathcal{L}$ 表示所有的语言，那么 $\mathcal{L}$ 不可数。因为 $\mathcal{L}$ 与 $\mathbb{R}$ 等势。回顾：语言是 $\mathcal{P}(\Sigma ^*)$ 当中的一个元素，即 $\Sigma^*$ 的每一个子集都是一个语言。用一个无限长的二进制串表示 $\Sigma^*$ 当中的第 $i$ 个元素是否包含在这个语言（子集）当中。那么这些二进制串就与语言形成双射。像之前证明 $\mathbb{R}$ 不可数一样（小数点后有无限个数字），同理可以证明 $\#\mathcal{L} = \#\mathbb{R} = 2^{\#\mathbb{N}}$。不过，$\Sigma ^*$ 是可数的。因为 $\mathcal{L} = \mathcal{P}(\Sigma^*)$，所以 $\#(\Sigma^*) = \#\mathbb{N}$。
令 $\mathcal{M}$ 表示所有的图灵机，那么 $\mathcal{M}$ 是可数的。因为 ${\langle M \rangle \mid M \text{ 是图灵机}} \subseteq \Sigma^*$ 。而 $\Sigma^*$ 是可数的，所以它的子集也是可数的。至于说为什么 $\Sigma^*$ 可数，是因为 $\Sigma^* = \{ \epsilon, 0, 1, 00, 01, 10, 01, 000, 001, \cdots \}$，能一个一个的列出来，所以是可数集。
存在不可判定的语言。因为语言比图灵机多（因为 $\#\mathcal{L} > \#\mathcal{M}$）。

用对角化方法证明：语言 $A_\text{TM} = \{ \langle M, w \rangle \mid \text{图灵机 } M \text{ 接受字符串 } w \}$ 不可判定

用反证法。先假设 $A_\text{TM}$ 是可判定的，也就是存在一台判定器 $H$ 判定它：$$H(\langle M, w\rangle)= \begin{cases}\text {接受} & \text { 若 } M \text { 接受 } w \\ \text {拒绝} & \text { 若 } M \text { 拒绝 } w \end{cases}$$。

然后再构造一个新的图灵机 $D$，$$D(\langle M\rangle)= \begin{cases}\text {接受} & \text { 若 } M \text { 拒绝 }\langle M\rangle \\ \text {拒绝} & \text { 若 } M \text { 接受 }\langle M\rangle\end{cases}$$。

然而由于 $M$ 是随便的一个图灵机，所以 $\langle M \rangle$ 可以替换成 $\langle D \rangle$ 作为 $D$ 的输入：$$D(\langle D\rangle)= \begin{cases}\text {接受} & \text { 若 } D \text { 拒绝 }\langle D\rangle \\ \text {拒绝} & \text { 若 } D \text { 接受 }\langle D \rangle\end{cases}$$。

观察这个式子：$D$ 拒绝 $\langle D \rangle$ 的条件下，反而要让 $D$ 接受输入 $\langle D \rangle$，这是一个矛盾。因此，图灵机 $H, D$ 是不存在的。所以不存在能够判定语言 $A_\text{TM}$ 的图灵机。所以语言 $A_\text{TM}$ 是不可判定的。

为什么说这种证明是使用了对角化方法？因为可以用这张图来描述证明过程。

当 $D$ 在这里面，对角线上的 $?$ 的就会产生矛盾，因为这个位置的值要与这一列上下划线标注的值相反，于是他就要跟自己相反~这…听起来就是个怪怪的矛盾。

由于队列自动机可以模拟图灵机，所以还可以推出：语言 $A_\text{QA} = \{ \langle B, w \rangle \mid B \text{ 是一个队列自动机，且接受 } w \}$ 也是不可判定的。

图灵不可识别语言

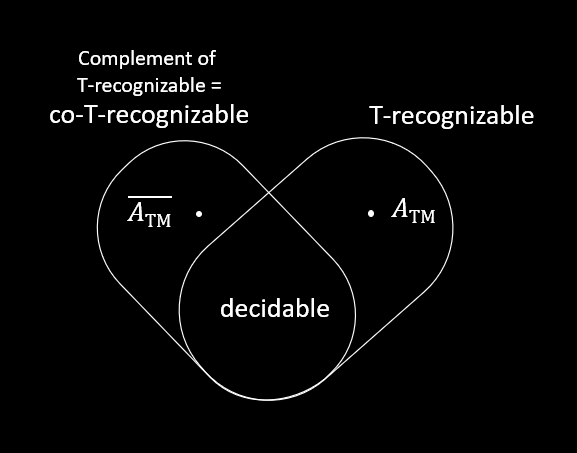
定义一个语言如果是图灵可识别的语言的补集，那么这个语言是 补图灵可识别的（co-T-recognizable）。

定理：语言 $A$ 是可判定的，当且仅当 $A$ 与 $\overline A$ 都是图灵可识别的，即 $A$ 既是图灵可识别的，也是补图灵可识别的。正方向比较简单，下面考虑反方向的证明思路：构建图灵机 $M_1, M_2$ 分别识别 $A, \overline A$，再构建一个图灵机 $T$ 判定 $A$。$T$ 对于输入 $w$，并行的在 $M_1, M_2$ 上运行 $w$，直到其中一个进入接受状态。如果 $M_1$ 进入了接受状态就接受，如果 $M_2$ 进入了接受状态就拒绝。因为对于任意一个串，要么在 $A$ 里面，要么就在 $\overline A$ 里面，所以 $M_1$ 和 $M_2$ 当中一定会有一个接受，于是 $M$ 就会停机。意味着 $M$ 不会永远运行下去，是一个判定器。所以 $A$ 是可判定的。

推论：$\overline{A_\text{TM}}$ 是图灵不可识别语言。因为 $A_\text{TM}$ 可识别但不可判定。

封闭性

推论：图灵可识别语言，在补运算下不封闭。事实上，图灵可识别语言，除了补运算，全都封闭（并、连接、星号、交）。

交：构建一个图灵机，含有两个子图灵机，当两个子图灵机都接受，才接受
并：构建一个图灵机，含有两个子图灵机，当两个子图灵机有一个接受，就接受
连接：非确定性的枚举所有的位置（$|w|+1$ 个分割点），把串分成前后两部分，如果有一种枚举方案，两部分都接受了，就接受
星号：类似连接运算，只是连接的方案更多罢

特殊的，对于可判定语言，在并交补连星五种运算下，全都是封闭的。

详细证明可以参考这份公开幻灯片。