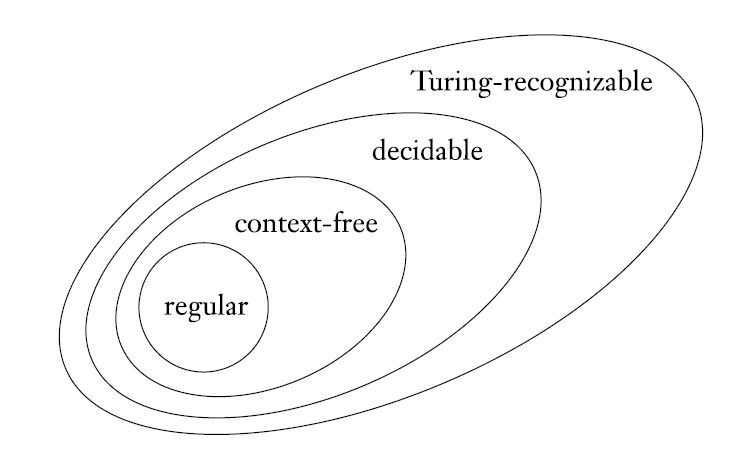
Lecture 5. Decidability 可判定性

与正则语言相关的可判定性问题

用语言 $A_\text{DFA} = \{ \langle B, w \rangle \mid B \text{ 是 DFA 且接受 } w \}$ 表示包含了所有 DFA 的编码以及 DFA 接受的串的编码。于是，DFA $B$ 能否接受输入串 $w$，等价于串串 $\langle B, w \rangle$ 是否属于语言 $A_\text{DFA}$。

定理：$A_\text{DFA}$ 是可一个判定语言，decidable。要证明，只需要构建一个判定器 $D_1$。用自然语言描述这个判定器就算：对于输入 $\langle B, w \rangle$，以 $w$ 作为输入模拟 DFA $B$，若模拟以接受状态结束则接受；若以非接受状态结束则拒绝。证毕。

类似地，$A_\text{NFA}$ 也是可一个判定语言。毕竟 NFA 与 DFA 是等价的。要证明，只需要设计一个图灵机（判定器）$D_2$，把输入的 NFA 转换成 DFA，然后传给上一个问题的判定器 $D_1$ 就好了。证毕。

类似地，$A_\text{REX} = \{ \langle R,w \rangle \mid R \text{ 是正则表达式且派生 } w \}$ 还是一个可判定语言。因为正则表达式可以转换成 NFA。那么要证明，只需要构造一个图灵机（判定器）$D_3$，把输入的正则表达式转换成与之等价的 NFA，然后再交给上一问的图灵机 $D_2$，让它转成 DFA，于是又回到了第一个问题。证毕。

综上，DFA、NFA 是否能识别一个串，以及正则表达式是否能派生一个串，这三个问题都是可判定的。

语言 $E_\text{DFA} = \{ \langle B \rangle \mid B \text{ 是 DFA，且 } L(B) = \emptyset \}$，表示 $B$ 识别的语言是空的（不接受任何串串）的 DFA 的编码的集合。相当于这个 DFA 从起始状态到接受状态，找不出任何的路径。只要又任意一条路径能从起始状态连接到接受状态，那么这个 DFA 接受的语言就不是空的。

定理：$E_\text{DFA}$ 依然是一个可判定的语言。这个图灵机（判定器）$D_4$ 和之前构造的那个判定无向图是否联通的几乎完全一样，只是变成了有向图而已。最后看看接受状态有没有被标记就好了。证毕。

语言 $EQ_\text{DFA} = \{ \langle A, B \rangle \mid A \text{ 和 } B \text{ 都是 DFA 且} L(A) = L(B) \}$，表示识别同一个语言的俩 DFA 的编码的集合。若两个 DFA $A, B$ 识别相同的语言，则 $\langle A, B \rangle \in EQ_\text{DFA}$。也即是说，这个语言表示 $A, B$ 是否识别相同的语言。

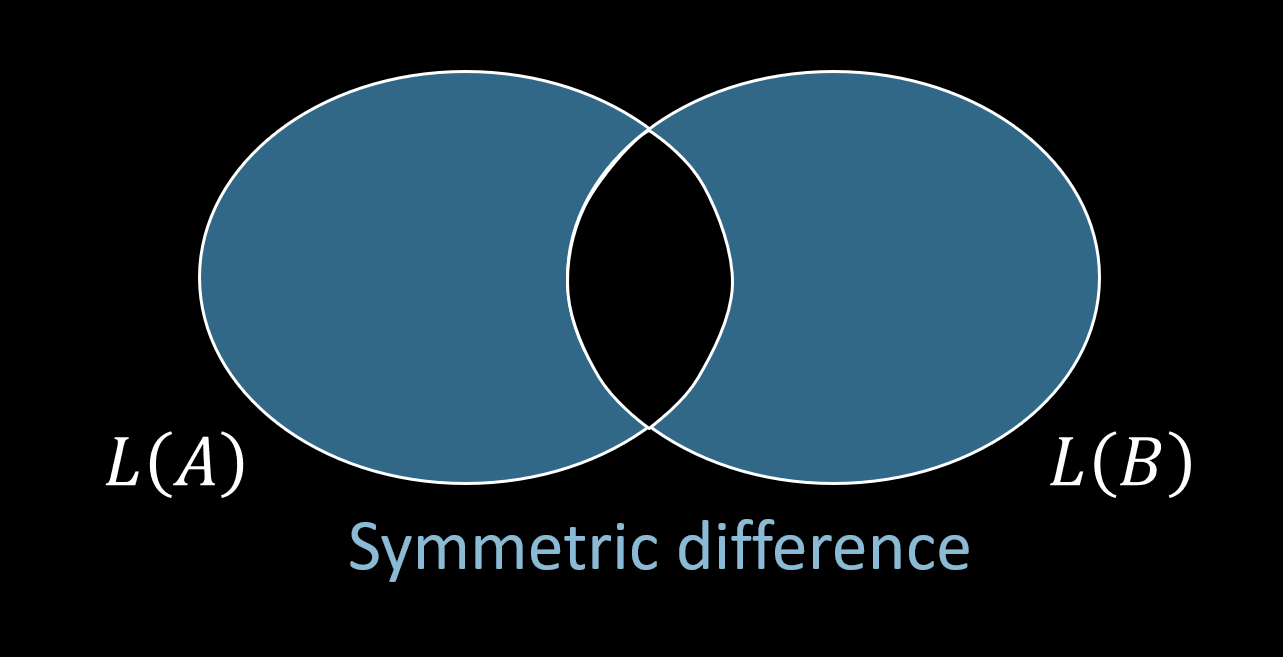
定理：$EQ_\text{DFA}$ 还是一个可判定的语言。证明思路是：如果 $L(A)$ 和 $L(B)$ 不相等，那么一定能分成两种情况，一种是 $L(A)$ 包含但 $L(B)$ 不含，另一种就是 $L(A)$ 不含但是 $L(B)$ 包含。于是，判定器 $D_5$ 要做的就是：把这两种情况并起来，得到 $L(C) = (L(A) \cap \overline{L(B)}) \cup (\overline{L(A)} \cap L(B))$。然后，只需要在判定器 $D_4$ 上面执行 $\langle C \rangle$，即看看 $L(C)$ 是不是空语言。如果是（即 $D_4$ 接受了 $\langle C \rangle$，那就说明 $L(A) = L(B)$），那么 $D_5$ 接受，否则拒绝。

乔姆斯基范式 Chomsky Normal Form

乔姆斯基范式，就是所有的替换规则都要么是 $A \rightarrow BC$ 要么是 $B \rightarrow b$ 的形式。也就是说，所有替换规则都是一个变元变成俩，或者一个变元变成终结符的形式。此外，允许存在 $S \rightarrow \epsilon$ 的规则，但是 $S$ 不能是起始变元。

定理 1：每一个 CFG 都可以转换成乔姆斯基范式。

定理 2：如果 $H$ 在 CNF 当中，且 $w \in L(H)$，那么所有 $w$ 的派生过程，都需要 $2 |w| - 1$ 步。可以用语法分析树来辅助理解。

与上下文无关语言相关的可判定性问题

语言 $A_\text{CFG} = \{ \langle G,w \rangle \mid G \text{ 是一个 CFG 且 } w \in L(G) \}$。一个 CFG $G$ 是否能派生字符串 $w$，等价于 $\langle G, w \rangle$ 是否属于语言 $A_\text{CFG}$。

定理：语言 $A_\text{CFG}$ 是可判定的。证明思路是：先把 CFG $G$ 转化为乔姆斯基范式的形式；然后尝试一遍所有步骤为 $2|w|-1$ 的派生过程，如果任意一个能成功派生 $w$ 则接受，否则拒绝。

语言 $E_\text{CFG} = \{ \langle G \rangle \mid G \text{ 是一个 CFG 且 } L(G) = \emptyset \}$。

定理：语言 $E_\text{CFG}$ 是可判定的。证明思路是，把 CFG 想象成一个语法分析树。从叶子节点（终结符）开始，反向找连通块。就像之前标记无向图连通分量一样。如果最终起始变元被标记了，那么就意味着起始变元能达到任意一个终结符，意味着这个 CFG 产生的语言非空，则拒绝。如果起始变元没有被标记，意味着无法产生任何的串串，接受。

语言 $EQ_\text{CFG} = \{ \langle G, H \rangle \mid G, H \text{ 是 CFG，且 } L(G) = L(H) \}$。

定理：语言 $EQ_\text{CFG}$ 不是可判定的！因为 CFL 在交补运算下不封闭，所以不能用之前 $EQ_\text{DFA}$ 的思路证明出可判定性。习题 5.1 要求证明该语言不可判定（Lab 5）。

语言 $AMBIG_\text{CFG} = \{ \langle G \rangle \mid G \text{ 是一个有歧义的 CFG} \}$。

定理：语言 $AMBIG_\text{CFG}$ 不是可判定的！

语言 $A_\text{TM} = \{ \langle M, w \rangle \mid \text{图灵机 } M \text{ 接受字符串 } w \}$。

定理：虽然语言$A_\text{TM} = \{ \langle M, w \rangle \mid \text{图灵机 } M \text{ 接受字符串 } w \}$ 不是可判定的，但是，这个语言是图灵可识别的！证明思路是设计一个图灵机 $U$，在输入串 $w$ 上面模拟 $M$，若 $M$ 以接受状态结束则 $U$ 接受，若 $M$ 永远运行或者进入拒绝状态则 $U$ 也拒绝。

上面的这个图灵机 $U$ 又叫做通用图灵机（universal），因为它可以模拟任何其他的图灵机。

由此可见，「可判定」比「图灵可识别」更加严格。