Lecture 4. Turing Machines 图灵机

图灵机与有穷自动机的区别

图灵机既能读也能写
图灵机的读写头，可以向左右两边移动（但是只能挪一个格子）
图灵机的带子长度无限
图灵机进入接受状态或拒绝状态则立即停机
图灵机在任意时刻都可以进入接受或拒绝状态，不一定是要在输入结束的时候

图灵机形式化定义

图灵机是一个七元组 $\left( Q, \Sigma, \Gamma, \delta, q_0, q_{\text{accept}}, q_{\text{reject}} \right)$，其中，$Q, \Sigma, \Gamma$ 都是有穷集，且：

$Q$ 是状态集
$\Sigma$ 是输入字母表。特殊空白符号 $\sqcup \not \in \Sigma$
$\Gamma$ 是纸带的字母表。输入字母表是纸带字母表的子集，即 $\Sigma \subseteq \Gamma$ 且特殊空白符号 $\sqcup \in \Gamma$（于是应该能推出 $\Sigma \subset \Gamma$）。
$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\}$ 是转移函数。即：当机器处于状态 $q$，读写头所在的带子位置的符号是 $a$，则当 $\delta(q, a) = (r, b, L/R)$ 时，机器写下符号 $b$ 来取代 $a$，进入状态 $r$，并让 读写头 向左或者向右移动。更进一步：如果要弄一个非确定性的图灵机，把转移函数改成 $\delta: Q \times \Gamma \rightarrow \mathcal{P}\left(Q \times \Gamma \times \{L, R\}\right)$，也就是像 DFA 到 NFA 或者 PDA 到 NPDA 的转变一样，弄一个幂集出来，这样每一步的转移都可以是一个集合，意味着有多个分支。
$q_0 \in Q$ 是起始状态，$q_{\text{accept}} \in Q$ 是接受状态，$q_{\text{reject}} \in Q$ 是拒绝状态，且 $q_{\text{accept}} \not= q_{\text{reject}}$

初始状态下，图灵机带子上从左到右前 $n$ 个格子填写了输入串 $w_1w_2 \cdots w_n \in \Sigma ^ $，其余部分保持空白。然后读写头从 最左边 的位置开始移动（根据转移函数描述的规则）。如果读写头已经处于最左边但是还有向左移动的指令，则停在原地不动。一旦进入接受状态或拒绝状态则立即停机（halt）*，否则永远持续运行（永远运行，即永不进入接受状态，相当于拒绝了）。

不过图灵机的这种形式化定义显得太麻烦了，所以有时候直接用自然语言描述会更简单。比如，刚刚证明过的 $B=\{0^k 1^k 2^k \mid k≥0\}$ 不是 CFL，这里设计一个图灵机来识别它。这个图灵机的工作流程可以用自然语言描述如下：

从左到右读完整个输入，直到遇到第一个 $\sqcup$ 代表输入结束。读的时候检查这个读入是否是 $0^*1^*2^*$ 的形式。如果不是，立即拒绝
读写头回到左端点
从左往右扫描。将第一个 $a, b, c$ 划掉（即用 $\not a, \not b, \not c$ 来代替，不是擦除）：
如果替换的 $a, b, c$ 都是最后一个，则进入接受状态
如果 $a, b, c$ 当中，有的是最后一个，有的不是最后一个，意味着数量不相等，进入拒绝状态
如果 $a, b, c$ 都还有剩余，则重复这个过程

一点新概念

图灵机 $M$ 接受的字符串的集合，就是被 $M$ 识别的语言，记作 $L(M)$。

如果一个语言能被图灵机识别，则称这个语言是 图灵可识别的（Turing-recognizable）。此外，一个语言是图灵可识别的，当且仅当存在一台 队列自动机（queue automaton） 识别（类似下推自动机，栈换成了队列）它。此外，还有的课本，把图灵可识别的语言称为递归可枚举语言，因为一个语言是图灵可识别的，当且仅当它是递归可枚举的。

如果一个图灵机对于任何输入，都永不无限运行，则这个图灵机称为 判定器（decider）。假如判定器 $M$ 可以识别语言 $A$，则称 $M$ 判定 $A$。如果一个语言能被某个判定器判定，则称这个语言是 图灵可判定的（Turing-decidable），简称 可判定的（decidable）。

图灵可判定比图灵可识别的定义更加严格，因此图灵可判定的语言的集合，是图灵可识别的语言的集合的子集。同时，CFL 也是图灵可判定的集合的子集，正则语言是 CFL 的子集。

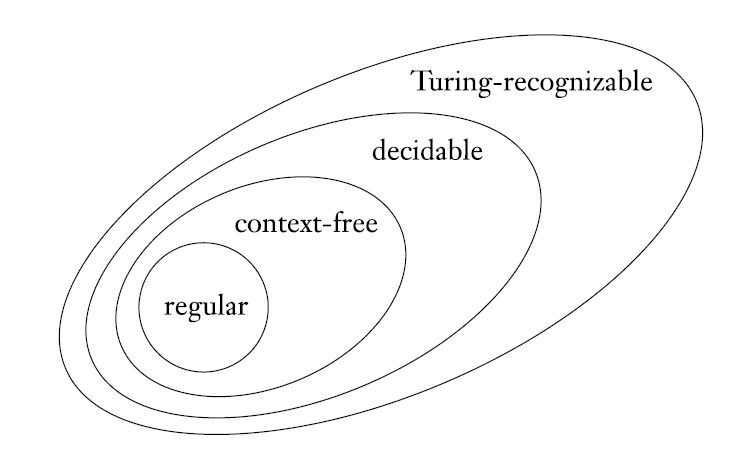
这张关系图会在「可判定性」章节中继续讨论。

格局

图灵机有一个新的概念叫做 格局（configuration），是指（当前状态、当前纸带内容、读写头位置）三者的结合。

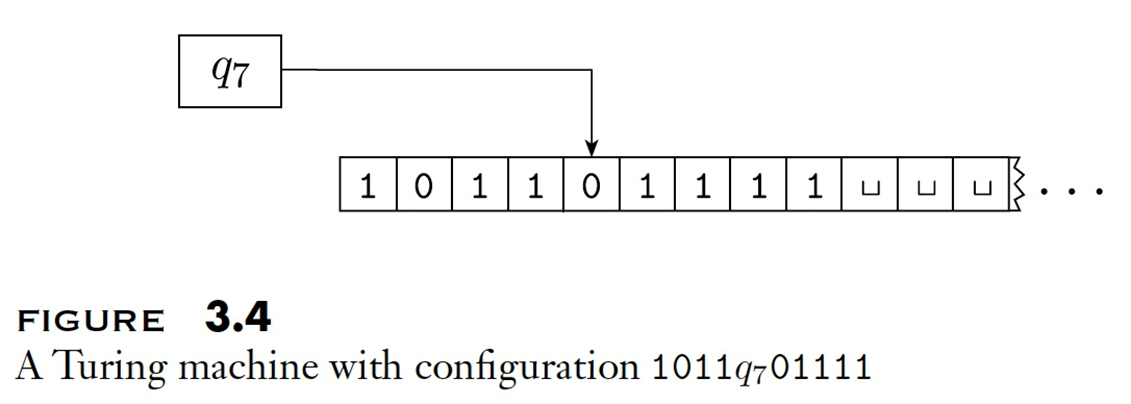
格局可以用 $u, q, v$ 表示：$q$ 表示当前状态，$uv$ 是当前纸带上的字符串（即 $u$ 连接 $v$），当前的读写头在 $v$ 的第一个符号的位置，$v$ 以后的内容全都是空白符。

比如格局：$1011q_701111$ 表示：当前纸带内容是 $101101111$，状态是 $q_7$，读写头位于第二个出现的 $0$ 上。

如果图灵机能合法的从格局 $C_1$ 一步进入格局 $C_2$，则称格局 $C_1$ 产生（yields） 格局 $C_2$。

一个图灵机 $M$ 接受输入 $w$ 的条件是，存在一个格局的序列 $C_1, C_2, \cdots, C_k$，满足以下条件：

$C_1$ 是 $M$ 对于输入 $w$ 的起始格局（$q_0w$）
$\forall i < k, C_i$ 产生 $C_{i+1}$
$C_k$ 是接受格局（$uq_{\text{accept}}v$）

图灵机示例

语言 $A = \{0^{2^n} | n \geq 0\}$，即所有长度是 $2$ 的幂的仅含 $0$ 的串串。

识别这个语言的图灵机的自然语言描述如下：

从左往右扫描，每隔一个字符就划掉一个零
如果一个零都划不动，说明是 $0^{2^0}$ 的形式，接受
如果划完一遍之后，剩下奇数个零，拒绝
返回左端点，重复前三步

$q_1$ 既是起始状态，也类似递归的终止条件：必须遇到至少一个$0$，否则直接拒绝；一旦遇到 $0$ 就进入 $q_2$
$q_2$：$q_2$ 这个状态没有确定的是奇数还是偶数。第一次走到 $q_2$ 状态意味着当前已经遇到了确切的一个 $0$，所以不停往右边走，如果被叉掉了就跳过，一旦遇到 $0$ 就进入偶数状态 $q_3$；遇到右端点说明 $0$ 的个数是恰好一个，符合递归终止条件，接受。如果是从 $q_5$ 回来的，这时候 $q_2$ 的状态就变成了偶数个零，因为 $q_5$ 是从 $q_3$ 来的。
$q_3, q_4$：$q_3$ 是已经遇到偶数个 $0$ 的状态，$q_4$ 是奇数个 $0$ 的状态，两个奇偶互补，每隔一个 $0$ 叉掉一个，同时右移；$q_3$ 如果叉掉一个之后遇到右端点则进入 $q_5$，$q_4$ 遇到右端点说明 $0$ 的个数不是偶数，拒绝
$q_5$：$q_5$ 不管读到什么东西，都一直往左边跑，直到回到最左端点，进入 $q_2$ 状态

格局表如下。要记得格局的表示形式：$q_x$ 后面紧跟的才是当前读写头的位置。

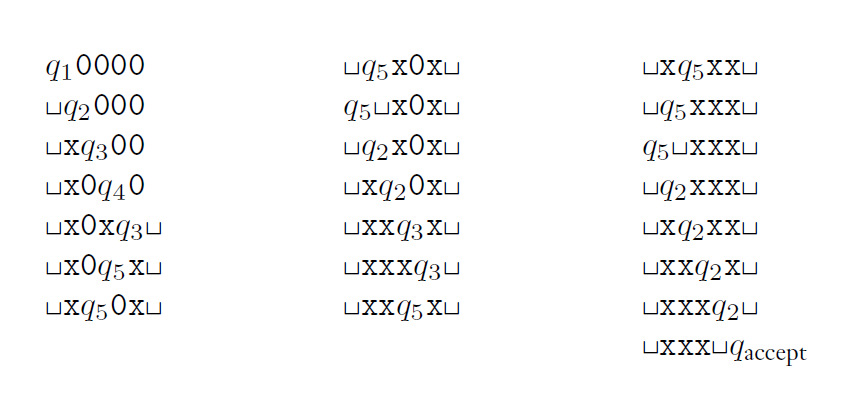
图灵机的变形

多带图灵机 Multi-tape Turing Machine

转移函数发生变化。对于 $k$ 条纸带的图灵机，转移函数是：$\delta: Q \times \Gamma^k \rightarrow Q\times \Gamma^k \times \{L,R,S\}^k$，其中 $S$ 是 stay 的意思，就是保持不动。也有的教材认为 $\delta: Q \times \Gamma^k \rightarrow Q\times \Gamma^k \times \{L,R\}^k$，就是必须挪走。

定理：每一个多带图灵机，都等价于一个单带图灵机。也就是可以用一个单带图灵机去模拟多带图灵机。

单带图灵机当中，用 $\#$ 来作为分隔符（delimiter），分割所有的纸带；头顶上有一圆点的表示每个纸带的读写头所在的字符。

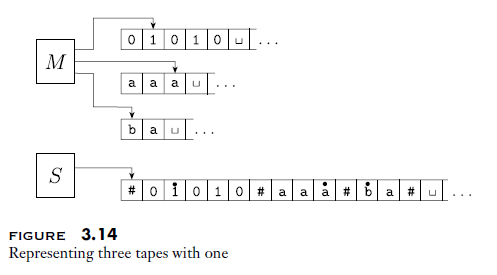
然而单带图灵机的控制器 S 会比多带图灵机的控制器 M 麻烦不少。

推论：一个语言是图灵可识别的，当且仅当存在一个多带图灵机识别它。

非确定性图灵机 Nondeterministic Turing Machine

转移函数变成了：$\delta: Q \times \Gamma \rightarrow \mathcal{P}\left(Q \times \Gamma \times \{L, R\}\right)$，幂集表示非确定性。

像 NFA 一样，非确定性图灵机的计算过程，也可以想象为一棵多叉树。不仅如此，每个非确定性图灵机和确定性图灵机也是等价的，即：每个非确定性图灵机也可以转化为一个确定性图灵机（状态个数变成 2 的幂）。

下图表示用确定性图灵机模拟非确定性图灵机。

推论：一个语言是图灵可识别的，当且仅当存在一个非确定性图灵机识别它。

推论：一个语言是可判定的，当且仅当存在一个非确定性图灵机判定它。

枚举器 Enumerator

枚举器就是附带了一个打印机的图灵机。打印机相当于一个输出设备。

枚举器的工作过程：

以空白输入的纸带开始运行
如果不停机，可能会打印出来无限多个串
枚举器 $E$ 所枚举的语言是最终打印出的所有串串的集合
$E$ 生成的串是任意顺序的，可能会有重复

定理：一个语言是图灵可识别的，当且仅当存在一个枚举器可以枚举它。

要证明当且仅当，需要从两个方向证明。

首先正向证明：如果有一个枚举器 $E$ 枚举语言 $A$，则能找到一个图灵机 $M$，识别这个枚举器枚举的语言。这个图灵机 $M$ 是这样的（对于输入串 $w$）
运行枚举器 $E$。每当 $E$ 打印了一个串，则与输入比较
一旦找到相同的，就接受

于是很显然的，$M$ 接受所有能被 $E$ 打印的串。证毕。

然后反向证明：如果有一台图灵机识别语言 $M$，则能找到一个枚举器 $E$ 可以枚举 $A$。这个枚举器的构造如下（忽略掉输入串）：
假设 $s_1, s_2, s_3, \cdots, s_i \in \Sigma ^*$ 是所有可能的串串，对于 $i=1, 2, 3, \cdots$，重复以下步骤：
对于 $s_1, s_2, s_3, \cdots$ 当中的每一个，$M$ 以其作为输入串，运行 $i$ 步。这大概是为了避免图灵机死循环
如果有计算接受，则打印出相应的 $s_j$
刚才这一坨看起来很麻烦，反正大概意思就是对于所有串串都运行一下图灵机 $M$，接受的全都输出

算法的定义

丘奇使用称为 $\lambda$ 演算（$\lambda$-calculus）的记号系统（notation system）来定义算法，图灵用图灵机来定义算法。这两个定义事实上是等价的。这两者之间的联系，叫做 丘奇图灵论题 Church-Turing Thesis。

令 $D = \{p \mid p \text{ 是有整数根的多项式}\}$，希尔伯特第十题要求设计一个算法，检测一个多项式是否具有整数根，相当于提问：$D$ 是否是可判定的。答案是，不存在检测多项式是否具有整数根的算法，因此 $D$ 不可判定。然而，$D$ 是图灵可识别的。

先考虑简单的情形。令 $D_1 = \{p \mid p \text{ 是有整数根 } x \text{ 的多项式}\}$，下面设计一个图灵机 $M_1$ 识别 $D_1$：

$M_1$ 的输入是一个关于变量 $x$ 的多项式 $p$，注意多项式是可以用字符串的形式来表示的
将 $x$ 赋值为 $0, 1, -1, 2, -2, 3, -3, \cdots$，不断地检查是否满足 $p=0$。如果满足，就接受。否则继续。

于是图灵机 $M_1$ 就设计出来了，因此 $D_1$ 是可识别的。然而这个图灵机可能会无限运行下去，因此不符合判定器的定义，于是 $D_1$ 不是可识别的。

假如多项式 $p$ 的变量个数不止一个，那也是类似，反正就不停的赋值然后试一下~

描述图灵机的术语 Terminology for Describing Turing Machine

描述图灵机有三种不同的级别。

最低等级是形式化的描述，就一堆数学式子，写出状态和转移函数，不过是最详细的
中档等级，称为 实现描述（implementation description），就是用自然语言描述图灵机怎么移动啊、怎么存储数据啊之类的，不指定状态和转移的细节
最高等级，是 高层次描述（high level description），同样是用自然语言来描述，但是连实现的细节都忽略了，也就是不提及如何管理纸带和读写头，相当于描述了一个算法

图灵机的记号

图灵机输入的都是字符串。如果要以其他对象（比如多项式、图）作为输入，就需要编码成字符串。

对象 $O$ 的字符串编码，用 $\langle O \rangle$ 表示。例如：$\{ \langle G \rangle \mid G \text{ is a connected undirected graph} \}$ 表示一个语言，包含所有的联通的无向图的编码串。

这里可以使用的无向图的编码格式是：(节点列表)((边), (边), (边), ...))

判定无向图是否联通的图灵机（判定器）的高层次描述是：

标记节点列表当中的第一个节点
重复第三步，直到无法再标记新的节点
任选一个节点，如果这个节点的一条边连接到一个已经被标记的节点，就把这个节点也标记上
检查，是否所有节点都被标记过。如果是，则接受，否则拒绝。