Lecture 3. Context Free Languages 上下文无关语言
上下文无关文法(Context Free Grammar,CFG)
上下文无关文法(CFG) 是一种 powerful 的描述语言数学模型,能够描述某些应用广泛的具有 递归 结构特征的语言。CFG 在编译器领域有重要应用。
上下文无关语言(CFL) 是与 CFG 相关的语言集合,包括所有的正则语言以及许多其他的语言类。
CFG 由一组 替换规则(substitution rule) 组成,替换规则也叫做 产生式(production)。每条规则从左到右,由一个符号、箭头和一个字符串组成,占一行。符号称作 变元(variable), 常用大写字母表示。 字符串由变元和 终结符(terminal) 组成,其中 终结符通常是小写字母、数字或特殊字符。第一条规则的左边,也就是 CFG 左上角的变元,称为 起始变元(start variable).例如,下面三行就表示了一个 CFG。
$$\begin{aligned} &A \rightarrow 0 A 1 \\ &A \rightarrow B \\ &B \rightarrow \# \end{aligned}$$
替换规则,顾名思义,就是把左边的替换成右边的。如:$A \rightarrow 0A1 \rightarrow 00A11 \cdots$。第一个写下的应当是起始变元。如此循环往复,可以产生许多字符串。直到写下的字符串没有变元,过程结束。产生的所有的字符串的集合,就是这个 文法的语言(language of the grammar)。上下文无关文法生成的语言叫做 上下文无关语言(CFL)。
语法分析树(parse tree) 可以形象的描述获取一个字符串的过程(派生 derivation)。如图。根节点是起始变元。语法分析树的阅读方法是:依次连接所有叶子节点。
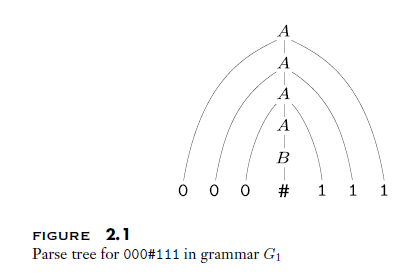
CFG 的形式化表述
CFG 是一个四元组 $G = (V, \Sigma, R, S)$,其中:
- $V$ 是变元的集合,有穷
- $\Sigma$ 在这里不是字母表,而是 终结符 集合,有穷。注意,$\Sigma \cap V = \emptyset$,即这两个集合不交。
- $R$ 是规则的集合,有穷。每条规则都是一个变元、一个字符串,而字符串中也可以包含变元,即:$V \rightarrow (V \cup \Sigma)^*$。
- $S \in V$,是起始变元
设字符串 $u, v \in (V \cup \Sigma)^$。若经过一次变换可以从 $u$ 生成 $v$,记作 $u \Rightarrow v$。若经过多次变换可以生成,记作 $u \stackrel{} \Rightarrow v$。而如果 $u=S$,称 $u$ 派生(derive) $v$。
那么这个 CFG 的语言就是:$L(G) = \{w\in\Sigma^* \mid S \stackrel{*}\Rightarrow w \}$
注意,在上文当中,替换规则的箭头都是单箭头,表示可经替换得到的箭头都是双箭头。
歧义性(ambiguity)
如果一个字符串能用两个(或者更多) 方式生成,就会对应着两个或者更多的语法分析树。此时这个语法就是有歧义的。
一般来讲,替换规则越多,越不容易有歧义。~~比如,CCPC 比赛规则就很有歧义性,但凡加上几句解释都不会被挂知乎暴喷~~
下推自动机 Pushdown Automata(PDA)
我们主要讨论 非确定型 的下推自动机。
PDA 附带一个栈。这个栈可以提供 无限 的存储空间。这个栈就像是一个笔记本,可以用来记录中间数据。push 操作就是 write-add,pop 操作对应 read-remove。因此,PDA 可以识别一些非正则的语言。
下推自动机能力上与上下文无关语法等价。因此,要证明一个语言是上下文无关的,既可以写出生成它的 CFG,也可以写出识别它的 PDA。
非正则语言 $B = \{0^n1^n \mid n \geq 0\}$ 可以用 PDA 来描述(泵引理那一节证明过非正则性),步骤如下:
- 从输入当中读取 0,并把 0 push 到栈里面去,直到遇到 1
- 从输入当中读取 1,每遇到一个 1 就 pop 一个 0
- 输入结束的时候,当栈空,则进入接受状态,此时 0 和 1 的数量相等。
PDA 的形式化表达
PDA 可以用六元组 $(Q, \Sigma, \Gamma, \delta, q_0, F)$ 来形式化表述:
- $Q$ 是 有限 状态集。
- $\Sigma$ 是输入字母表,$\sqcup \not \in \Sigma$
- $\Gamma$ 是栈字母表,$\sqcup \in \Gamma$,$\Sigma \not= \Gamma$
- $\delta$ 是转移函数,$\delta: Q \times \Sigma_{\epsilon} \times \Gamma_{\epsilon} \rightarrow \mathcal{P}(Q \times \Gamma_{\epsilon})$,例如 $\delta(q, a, c) = \{(r_1, d), (r_2, e)\}$。这里的 幂集是非确定性的一种体现,因为下一步可能有多个动作。
- $q_0 \in Q$ 是起始状态
- $F \subseteq Q$ 是接受状态集
PDA 的一个例子(体现非正则性)
以刚才提到过的语言为例,识别 $B = \{0^n1^n \mid n \geq 0\}$ 的下推自动机就是:
- $Q = \{q_1, q_2, q_3, q_4\}$
- $\Sigma = \{0, 1\}$
- $\Gamma = \{0, € \}$
- $F = \{q_1, q_4\}$
其中:
- $q_1$ 是初始状态,也是没有输入的情况下的接受状态
- $q_2$ 是一直读 0
- $q_3$ 是一直读 1
- $q_4$ 是 0 被删光了的接受状态
- $\$$ 表示栈底的一个标记。当 PDA 遇到 €,就知道当前的栈空了。
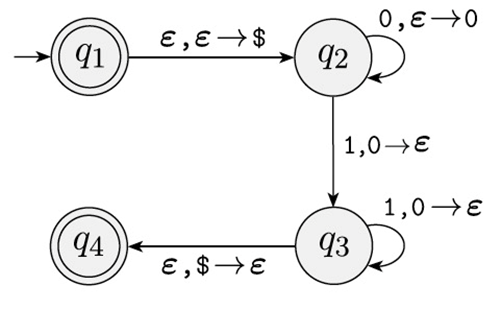
注意,PDA 的每个转移都标注了 $z, x \rightarrow y$,其中 $z$ 是读取的符号,而 $x \rightarrow y$ 的意思是用 $y$ 来替换栈顶的 $x$。如果 $x = \epsilon$ 则代表着入栈,如果 $y = \epsilon$ 则代表着出栈。
PDA 的另一个例子(非确定性的 PDA)
对于语言 $C = \{ww^{\mathcal{R}} \mid w \in {0, 1}^*\}$。注意,$w^{\mathcal{R}}$ 表示字符串 $w$ 的 reverse。即,语言 $C$ 当中的所有字符串都是中心对称的。
对于识别 $C$ 的 PDA,工作过程可以这样通俗的描述:
- 读入符号,并把它推入栈中;非确定性的 重复这一步骤或进入步骤 2(可以想象为 bfs 双线程分头跑)
- 读入符号,并弹出栈顶符号。如果读入的与栈顶符号一致,则继续,否则终止这个「线程」。
- 空栈,进入接受状态。
在示意图当中,$q_2$ 到 $q_3$ 的 $\epsilon, \epsilon \rightarrow \epsilon$ 体现了这一非确定性,表示什么都不做就从 $q_2$ 走到了 $q_3$。
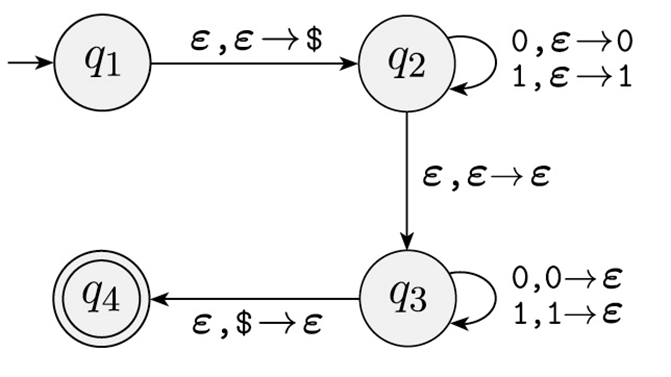
CFG 与 PDA 的等价性(CFG 转 PDA)
引理:若 $A$ 是一个上下文无关语言(CFL),则就会有一台下推自动机(PDA)识别 $A$。
证明思路:根据 CFL 的定义,存在一个 CFG 来生成它。只需证明这个 CFG 可以转换成一个 PDA。
过程大概就是:
- 首先,将 $\$$ 和起始变元压入栈中,然后重复下面过程
- 读取栈顶符号。
- 若栈顶符号是一个变元,则 非确定 地选择一条替换规则,将这个变元替换成对应的字符串
- 若栈顶符号是一个终结符,则将这个终结符与字符串当前符号进行比较;若相等,弹出栈顶,则继续这个过程,否则这个分支拒绝。
- 若栈顶符号是 $\$$,表示栈空。如果此时字符串已经读取完毕,则接受这个输入的字符串。
下图形象化的描述了这个过程(的前几个步骤)
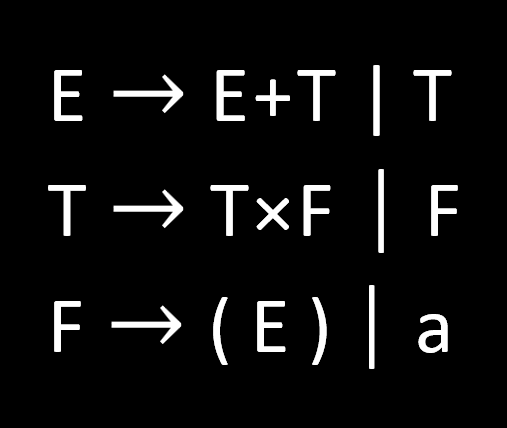
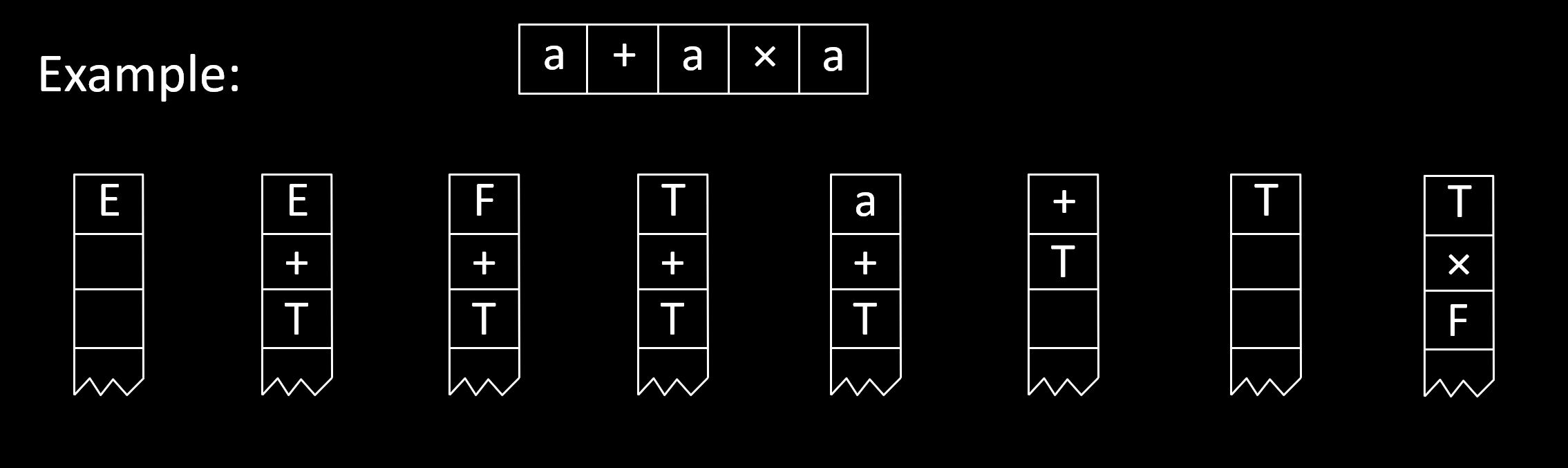
还有一堆定理
- 语言 $A$ 是上下文无关语言,当且仅当存在一台 PDA 识别 A。 对于这个定理,从左到右已经证明过,从右到左的证明非常复杂,无需掌握,只需要记住这个结论就好了。
- 由于 PDA 比 DFA/NFA 多了一个栈,所以比 DFA/NFA 更强。因此,所有能被 DFA/NFA 识别的语言,一定能被 PDA 识别。也就是说,所有的正则语言都是上下文无关语言。
- 若 $A$ 是一个上下文无关语言,$B$ 是一个正则语言,则他们的交($A \cap B$)是上下文无关语言(CFL)。 这意味着,CFL 在交运算下不封闭。一个例子:$L_1 = \{0^*1^*\}$ 是正则语言,$L_2 = \{0^n1^n, n\geq 0\}$ 是上下文无关语言,而 $L = L_1 \cap L_2 = L_2$ 是上下文无关。因为下推自动机的状态可以同时模拟 $A$ 的下推自动机的状态和 $B$ 的有限状态机的状态,而下推自动机的栈可以用来模拟 $A$ 的下推自动机的栈。然而,CFL 和 CFL 的交,不一定是 CFL。因为一个栈无法模拟两个栈。也就是指。CFL 在交运算下不具有封闭性。
- ??????无法理解上一条。为啥交出来不是正则语言?可能,这里的交不是指集合直接交,而是指所有的串的交,而正则/上下文无关是针对语言(集合)的,而不是针对串的?
针对第四点的疑问,可以想象:A 组三人组队打 ACM 可以拿金牌,B 组三人组队打 ACM 也可以拿金牌。此时 AB 当中抽三人出来再组队,应该也能拿金牌(是 CFL)。然而如果某一天 B 组变成了 100 个人,有 97 个混子。这时候再总 AB 当中抽三人(交)出来组队,就不一定拿金牌了(非 CFL)
也曾经跟 廖智炫 讨论过这种相交运算的问题。
跟 廖智炫 的聊天记录
BUAA 卡绒熊 廖智炫 龙岩 14:23:01 集合布尔运算
BUAA 卡绒熊 廖智炫 龙岩 14:23:10 只有在正则语言上才是封闭的
BUAA 卡绒熊 廖智炫 龙岩 14:23:13 其他是不保证的
提子开花 14:23:19 或者说 正则 ∩ CFL,是 CFL
提子开花 14:23:24 但是正则是 CFL 的子集啊
提子开花 14:23:36 子集∩全集,不应该还是子集本身吗
BUAA 卡绒熊 廖智炫 龙岩 14:23:43 不是啊
BUAA 卡绒熊 廖智炫 龙岩 14:24:01 是正则运算自己是封闭的
BUAA 卡绒熊 廖智炫 龙岩 14:24:11 正则交cfl
BUAA 卡绒熊 廖智炫 龙岩 14:24:23 说的不是所有正则语言和所有cfl的交
BUAA 卡绒熊 廖智炫 龙岩 14:24:34 你说的往往是某个正则语言和某个cfl的交
BUAA 卡绒熊 廖智炫 龙岩 14:25:08 这样交出来是语言上的交
BUAA 卡绒熊 廖智炫 龙岩 14:25:11 所以是cfl
BUAA 卡绒熊 廖智炫 龙岩 14:25:19 所谓正则语言是cfl的子集
BUAA 卡绒熊 廖智炫 龙岩 14:25:38 是指所有正则语言都是cfl,但不是所有cfl都是正则的
BUAA 卡绒熊 廖智炫 龙岩 14:25:50 这时候交指的是集合上的交
跟 廖智炫 的另一段聊天记录
BUAA 卡绒熊 廖智炫 龙岩 21:50:33 我刚刚把这个问题想清楚了
BUAA 卡绒熊 廖智炫 龙岩 21:50:35 是这样的
BUAA 卡绒熊 廖智炫 龙岩 21:50:50 我们常说的正则语言交CFL是CFL
BUAA 卡绒熊 廖智炫 龙岩 21:51:07 指的其实是,一个正则语言,交一个CFL,是一个CFL
BUAA 卡绒熊 廖智炫 龙岩 21:51:22 比如字符集是ASCII码
BUAA 卡绒熊 廖智炫 龙岩 21:51:31 有一个正则语言是 (0|1)*
BUAA 卡绒熊 廖智炫 龙岩 21:51:52 有一个CFL是{ww| w=\Sigma*}
BUAA 卡绒熊 廖智炫 龙岩 21:52:05 那他们交出来的语言是一个CFL
BUAA 卡绒熊 廖智炫 龙岩 21:52:13 {ww| w=(0|1)*}
BUAA 卡绒熊 廖智炫 龙岩 21:52:34 但是按我们说的,正则语言也是CFL
BUAA 卡绒熊 廖智炫 龙岩 21:53:14 所以如果CFL是 0*2* ,那么交出来也是一个CFL, 0*
BUAA 卡绒熊 廖智炫 龙岩 21:53:23 这个时候就退化为正则语言内部的封闭运算
BUAA 卡绒熊 廖智炫 龙岩 21:53:32 但是我们说的正则语言是CFL的子集
BUAA 卡绒熊 廖智炫 龙岩 21:53:51 它的正则语言的含义是,所有正则语言构成的集合
BUAA 卡绒熊 廖智炫 龙岩 21:54:07 而这里的CFL指的也是所有CFL构成的集合
BUAA 卡绒熊 廖智炫 龙岩 21:54:39 所以这个时候,正则语言构成的集合,显然是CFL构成集合的子集,它交CFL构成的集合也确实是自己
BUAA 卡绒熊 廖智炫 龙岩 21:55:01 就是因为中文的语句压缩,导致同一个词汇含有不同的语义
提子开花 22:12:30 也就是说
提子开花 22:12:49 有时候 cfl 指的是,所有 cfl 的集合
提子开花 22:13:03 而有的时候,cfl 只是指一个语言
提子开花 22:13:04 吗
BUAA 卡绒熊 廖智炫 龙岩 22:13:12 对
提子开花 22:13:46 好像确实是这个道理
CFL 的封闭性
刚才已经指出,CFL 在 $\cap$ 下不封闭。
事实上,CFL 在 $\overline{}$ 运算下也不封闭。
但是 CFL 在 $\cup, \cdot, *$ 下封闭。
非上下文无关(泵引理)
泵引理:对于任意的上下文无关语言 $A$,存在一个泵长度 $p$,对于语言 $A$ 当中一个长度不小于 $p$ 的字符串 $s$,满足 $s$ 可以被分为五个部分即 $s = uvxyz$,满足:
- $\forall i \geq 0, uv^ixy^iz \in A$
- $vy \not= \epsilon$,
- $|vxy| \leq p$
也就是说, CFL $A$ 当中所有足够长的字符串,都能被抽取,且仍属于这个语言。
特别注意第二点:$v$ 和 $y$ 可以有一个是空串,不能俩都是空串。
这里的泵引理与正则语言的泵引理有一点不同。观察发现,这里把所有的长字符串切割成五个部分,而第二块和第四块(非空)重复相同次数之后仍属于这个语言。这大概对应着栈的记忆功能——每个 $y$ 对应一个 $v$。
泵引理的证明思路
需要画图辅助。
当一个 CFL 的串非常长,那么生成这个串的语法解析树就会非常高。语法解析树每一层都会有变元,而变元的数量是有限的。因此,从语法解析树的根节点到叶子节点的路径上,就会有一个变元重复出现,如图(R 是重复过的变元):
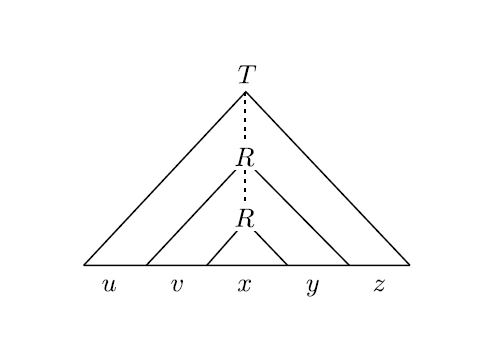
这就体现出字符串被分为五个部分。当然,下面那个变元 R 还继续扩张,于是可以再重复出现第三个 R:
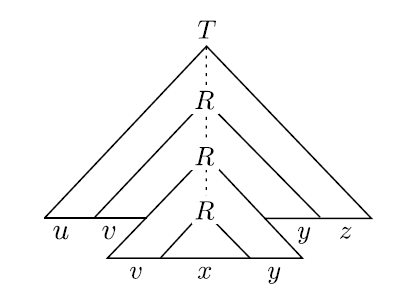
相当于,刚才的 $x$ 又被替换成了 $vxy$。所以 $v$ 和 $y$ 就可以作为字符串当中的可重复片段。类似地,如果把上面第一个 R 直接替换,就变成了 $uxz$ 即 $uv^0xy^0z$ 的样子。显然这个串也在 CFL 当中。
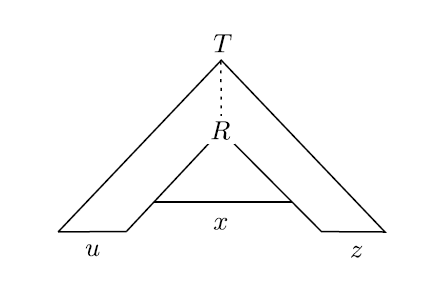
泵长度的选取
设解析树的树高是 $h$,由于希望有变元在路径上重复出现,根据鸽巢原理,所以一定要满足 $h > |V|$,$|V|$ 是指变元的个数。此外,设最长的一个替换规则是一个字符变成 $b$ 个字符,那么这棵树的叶子节点最多有 $b^h$ 个,也就是说 $|s| \leq b^h$。取 $p = b^{|V|} + 1$,那么 $|s| >= p > b^{|V|}$,也就是说 $|s| \in \left[b^{|V|}, b^h\right]$。
使用泵引理证明语言的非上下文无关性
注意
如果要证明非正则、非上下文无关,只能用泵引理。只需要找出一个特例 string 让它无法被泵出就可以了。无法泵出是指,不管怎么分割,都没法分成可以被复制粘贴后还存在于语言当中的 $xyz$ 或者 $uvxyz$。也就是说,需要找出一个 string,但是需要讨论这个 string 的所有可能的分割方案。
如果要证明正则性或者上下文无关,有多种方法:
- 构造与之对应的有穷自动机或者下推自动机
- 如果是 CFL,可以构造生成它的 CFG
- 利用运算性质,如正则与 CFL 的交还是 CFL
- 利用运算封闭性,如正则和 CFL 都在并、连接、星号运算下封闭
例一:证明语言 $B=\{0^k 1^k 2^k \mid k≥0\}$ 非上下文无关语言
用反证法证明。假设语言 $B$ 是上下文无关语言。
设泵长度是 $p$,取 $s = uvxyz = 0^p1^p2^p \in B$。由泵引理的第三条限制($|vxy| \leq p$)得知,$vxy$ 当中不能同时包含 $0$ 和 $2$ 两种字符(否则就会越过中间的 $p$ 个 $1$)。
所以假如把 $v$ 和 $y$ 复制粘贴多次(可能,$vxy = 1^p$),会导致得到的新串当中三种字符的个数不等($1$ 明显变多了)。也可能是 $0$ 和 $1$ 变多但 $2$ 没变多,或者 $0$ 没变多但 $1$ 和 $2$ 变多了。所以新串不可能保持 $0,1,2$ 个数相等。所以得到的新串就不属于这个语言。这与泵引理矛盾。
因此,$B$ 不是上下文无关语言。
题外话
给出两个语言 $A_1 = \left\{0^k 1^k 2^l \mid k, l \geq 0\right\}$,$A_2 = \left\{0^l 1^k 2^k \mid k, l \geq 0\right\}$。
显然这两个语言都是 CFL。
并且这两个语言的交恰好是 $B$,刚才证明了非上下文无关的 $B$。
这侧面说明了,CFL 在交运算下不具有封闭性。
例二:证明语言 $F=\{ww \mid w \in {0,1}^* \}$ 非上下文无关语言
还是反证法。
取 $s = 0^p1^p0^p1^p$,而 $|vxy| \leq p$,那么 $vxy$ 不能含有两段 $0$ 区间或者两段 $1$ 区间。
同时,$vxy$ 应当横跨 $s$ 的中点(否则一定抽不出来)
于是,$uv^2xy^2z$ 就会变成 $0^p1^i0^j1^p$ 的形式,而 $i\not=j$,从而导致 $0$ 和 $1$ 的个数不相等,所以这个串不属于语言 $F$。
故 $F$ 不是 CFL。
正则和上下文无关的泵引理比较
| 切分方式 | 非空限制 | 长度限制 |
|---|---|---|
| 正则 | $xy^iz$ | $y \not= \epsilon$ |
| 上下文无关 | $uv^ixy^iz$ | $vy \not= \epsilon$ |
注意,正则的长度限制是 $|xy| \leq p$,而 $x$ 是字符串的 起始。这一点很特殊。上下文无关的限制不是起始。