跳转至

Lecture 2. 非确定型有限状态机（Nondeterministic Finite Automata）

非确定型有限状态机（Nondeterministic Finite Automata，NFA）

新的性质：

  • 每个状态的转移函数，可能有多个不同的取值
  • 出现了 $\epsilon$ 转移，free move（DFA 中不存在）
  • 若存在任意一种路径到接受态，即认为接受这个 input

一个 NFA $N$ 是一个五元组 $(Q, \Sigma, \delta, q_0, F)$，几乎跟 DFA 一样，只是有一点改变：

$$\delta: Q \times \Sigma_{\epsilon} \rightarrow \mathcal{P}(Q) = \{R | R \subseteq Q\}$$

其中 $\mathcal{P}(Q)$ 是幂集。也就是说转移函数的值，在 DFA 中是一个状态，在 NFA 中是一堆状态的集合。

形象化的来讲，DFA 的每一步都是确定的，而 NFA 每一步可能有不少分支，如图。

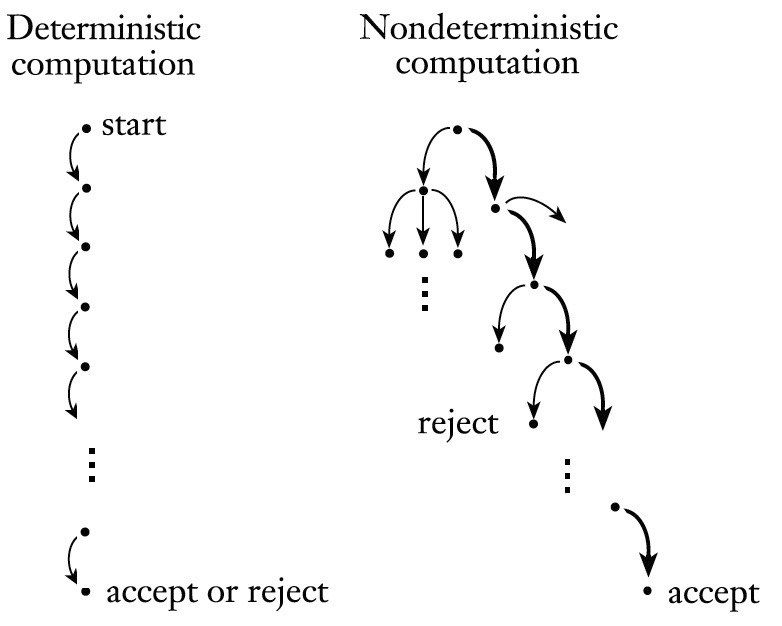
image-20220905113426409

NFA 到 DFA 的转换

定理：若 NFA 识别 $A$，则 $A$ 也是正则的。（之前已知，若 DFA 识别 $A$ 则 $A$ 正则）

要证明这个定理，只需证明，每一个 NFA 都能转换成 DFA，即 NFA 和 DFA 具有等价性。

NFA 和 DFA 的等价性

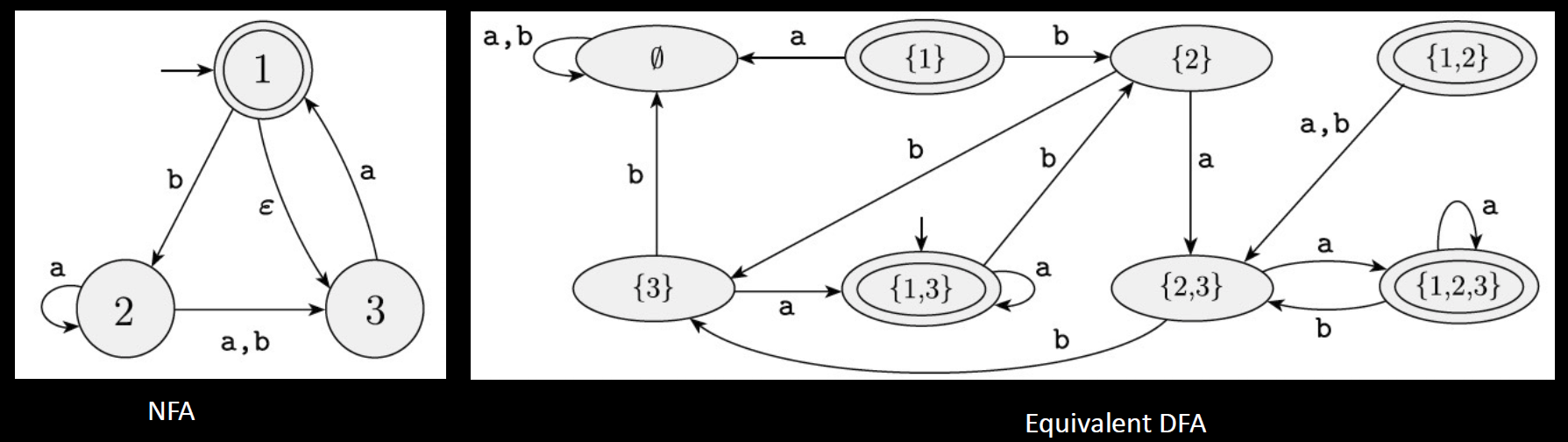
若 NFA 中有 $n$ 个状态，则与之等效的 DFA 中有 $2^n$ 个状态。DFA 的每一个状态都对应着 NFA 当中的一个状态子集。

原先的起始状态是 $1$，起始状态和从起始状态通过 $\epsilon$ 可以到达的状态合起来，只有 $1, 3$，于是转换到 DFA 之后的起始状态就是：$\{1,3\}$。

原先的接收状态是 $1$，则新的接受状态集，就是所有包含 $1$ 的状态子集，即：$\{1\}, \{1,2\}, \{1,3\}, \{1,2,3\}$，共四个。

观察规律得知，对于每一个转移符号，考虑当前 DFA 状态当中的每个元素对应的 NFA 当中的状态根据这个符号转移到的状态的集合的并集，就是 DFA 的下一个状态。如：对于状态 $\{2,3\}$ 和符号 a，由于 NFA 中 $2$ 可以从符号 a 转移到 $\{2,3\}$，而 $3$ 可以转移到 $1$，则并起来就得到了 DFA 的下一个状态：$\{1,2,3\}$。此外尤其注意 $\epsilon$ 的特殊性：如果转移到了某个状态，这个状态可以通过 $\epsilon$ 再转移到别的地方去，那么通过 $\epsilon$ 能得到的也应该加入集合。

特殊的，对于 DFA 中没有入度的状态，可以直接删除。

image-20220909140756110

正则表达式

定义：当 $R$ 满足以下条件之一，则是正则表达式

  • $R$ 是只包含字母表当中的一个单独符号的语言（如 $\{a\}$）
  • $R = \epsilon$（只包含空串的语言，即 $\{\epsilon\}$）
  • $R = \emptyset$（不包含任何串串的语言）
  • $R = R_1 \cup R_2$，其中 $R_1$ 和 $R_2$ 是正则表达式
  • $R = R_1 \circ R_2$，其中 $R_1$ 和 $R_2$ 是正则表达式
  • $R = R_1 ^*$，其中 $R_1$ 是正则表达式

通常，把 $R$ 描述的语言记作 $L(R)$。若 $L(R)$ 表示正则表达式 $R$ 描述的语言，那么 $L(R)$ 也是正则的。

正则表达式转 NFA

广义非确定型有穷自动机（Generalized Nondeterministic Finite Automaton，GNFA）

GNFA 与 NFA 类似，但是 GNFA 的转移符号可以是正则表达式。

为了方便起见，假设所有的 GNFA 均具有如下特性：（黑书 42 页，Slide2 第 16 页）

  • 起始状态没有入度（不能被转移到）；且起始状态可以转移到其他任何一个状态
  • 接收状态只有一个，且接收状态不等于起始状态；且接收状态没有出度（不能转移出去）；且接收状态可以从任何一个其他状态转移过来
  • 除了起始状态和接收状态，每个状态有一个转移到自己的箭头）（不一定是 $\epsilon$ 转移），且到任何一个其他状态都有箭头

DFA 到 GNFA 的转换

就描述能力而言，正则表达式与有穷自动机是等价的。因为任何正则表达式都可以转换成识别他的有穷自动机，反之亦然。

也就是说，DFA 能转化为正则表达式。从而，DFA 可以转化为 GNFA。

基于以上三点假设，很容易写出 DFA 转换到这种特殊 GNFA 的步骤：

  1. 添加一个新的起始状态，到原先的起始状态连接一个 $\epsilon$；原先的起始状态变成普通状态
  2. 添加一个新的接受状态，从原先的所有接受状态到新的这个接受状态连接一个 $\epsilon$；原先的接受状态变成普通状态
  3. 如果两个状态之间有多种不同的转移，则合并到并集，保留一个箭头
  4. 如果两个状态之间没有箭头转移，则添加一个 $\emptyset$ 的箭头。注意，这条箭头永远不会被经过。所以这一步不会改变语言。

然而这个好像不是重点。

GNFA 再到正则表达式的转换（递归）

把 $k$ 个状态的 GNFA 变成 $k-1$ 个状态的 GNFA，然后递归。当这个 GNFA 只剩下起始状态和接收状态，那么箭头上面写的东西就是要求的正则表达式。

设现在的 GNFA 有 $k>2$ 个状态，要构造一个含有 $k-1$ 个状态的 GNFA。只需任意挑选一个状态（不能是起始或接受状态），把它删掉。

如图（删掉了 $q_{\text{rip}}$，保留了 $q_i, q_j$，把被删状态 $q_\text{rip}$ 的自环做星号运算，然后按顺序连接起来，再跟原有的并起来）。

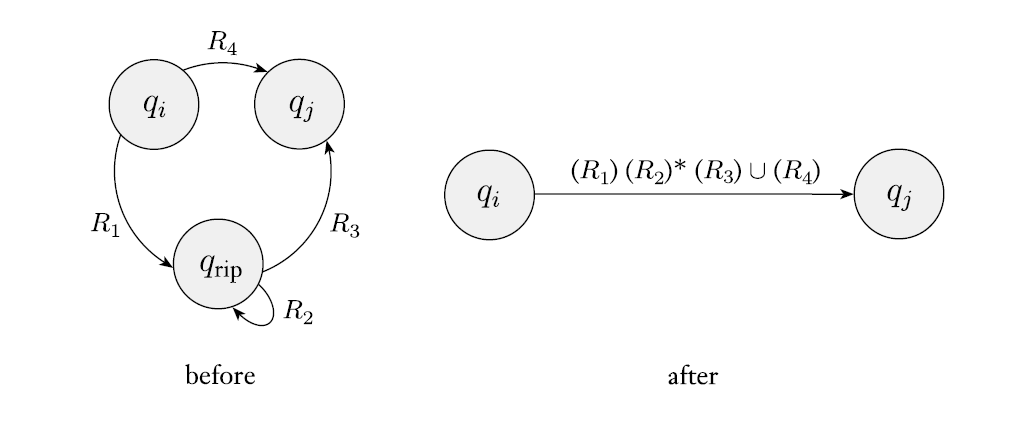
image-20220916234440299

于是，DFA 可以转换成 GNFA 进而转换成正则表达式。

GNFA 的定义

GNFA（广义非确定型有穷自动机）是一个五元组 $(Q, \Sigma, \delta, q_{\text{start}}, q_{\text{accept}})$，其中：

  • $Q$ 表示状态集，有穷
  • $\Sigma$ 是字母表
  • $\delta: (Q - \{q_{\text{accept}}\}) \times (Q - \{q_{\text{start}}\}) \rightarrow \mathcal{R}$ 是转移函数，其中 $\mathcal{R}$ 是字母表上所有正则表达式的集合。这个转移函数有一点怪，自变量是二元组，分别表示前一个状态和后一个状态；返回值是可以从这个前状态转移到后状态的正则表达式
  • $q_{\text{accept}}$ 和 $q_{\text{start}}$ 顾名思义，分别是接受态和起始态

泵引理（pumping lemma）

能被 DFA 识别的，就是正则语言。不能被识别的，就是非正则的。

泵引理指出，所有的正则语言，都具有一种特殊性质。因此可以用泵引理证明语言的正则性。

泵引理（pumping lemma）

泵引理：对于任意的正则语言 $A$，存在一个数，叫做泵长度 $p$，使得 $A$ 中任意一个长度大于 $p$ 的字符串 $s$ 都满足 $s = xyz$，其中：

  • $\forall i \geq 0, xy^iz \in A$
  • $y \not= \epsilon$
  • $|xy| \leq p$

泵引理的意思是说，语言中的所有字符串，只要 足够长（大于泵长度），就能够被抽取（pump）出来。抽取是指，在这个字符串当中，可以选取一段子串，重复任意次（得到 $xy^iz$），新串仍然在语言中。

考虑泵引理的证明思路。特殊情况下，若 $i=0$，显然成立。接下来分析 $i>0$ 的情况。设泵长度 $p$ 是 $M$ 的状态数，即自动机 $M$ 具有 $p$ 个状态。假如转移了 $q$ 次（$q > p$），根据鸽巢原理（pigeonhole principle），至少有一个状态被访问了两次。即，存在一种路径，从一个状态，转移几次之后，又回到了这个状态。这就对应了上面 $xy^iz$ 当中的 $y^i$。同时，$|xy|<=p$ 也被满足。

证明语言非正则性

例一：证明语言 $B = \{0^n1^n | n \geq 0\}$ 非正则（泵引理）

观察得知，语言 $B$ 当中的所有字符串，一定具有同等个数的 0 和 1.

先假设 $B$ 是正则语言。那么他就会满足泵引理。设 $p$ 是泵长度。取字符串 $s = 0^p1^p \in B$。

根据泵引理的第三条限制 $|xy| \leq p$，而 $s$ 开头又恰好有 $p$ 个 0，所以 $xy$ 只能含有 0，不能有 1；进一步推导出，$y$ 仅含 0 不含 1

于是 $xyyz$，$xyyyz$ 等字符串中，随着 $y$ 越来越多，0 就会越来越多（别忘了 $y \not= \epsilon$）0 的个数会比 1 多。所以这些串不在语言 $B$ 当中，与泵引理矛盾。故 $B$ 不是正则语言。

例二：证明语言 $F = \{ww | w\in {0,1}^*\}$ 非正则（泵引理）

依然先假设 $F$ 是正则语言，$p$ 是泵长度。注意到该语言的所有字符串，都是前一半和后一半相等的。取字符串 $s = 0^p10^p1 \in F$。

首先，$y$ 仅能由 $0$ 组成，因为 $|xy| \leq p$，而 $s$ 的开头有 $p$ 个 $0$，所以 $y$ 不可能含有 $1$。

于是 $xyyz$ 只能增加前一半串串的 $0$ 的数量，后一半串串的 $0$ 个数不变，于是前后 $0$ 的数量不i一直。所以 $xyyz \not \in F$，所以 $F$ 非正则。

bad case: $0^p0^p$，这个串也是 $C$ 的成员，但是能被泵出：只要找一个 $|y| = 2$ 的分割方法，$y^i$ 就可以左右两边各分配一半。

例三：证明语言 $C = \{w | w \text{ 中 0 和 1 的个数相等} \}$ 非正则（封闭性）

这个用泵引理很难证。

考虑正则运算的封闭性。已知 $0,1$ 是正则的，所以 $0^,1^$ 也是正则的，进而 $0^1^$ 是一个正则的语言。

前面例一已经证明过，$B = \{0^n1^n | n \geq 0\}$ 是非正则的。观察 $B, C$ 容易发现，$B = C \cap \{0^1^\}$。若 $C$ 正则，那么跟另一个正则语言求交，应该也是正则才对。所以 $C$ 是非正则的。