跳转至

L1. 数学初步与有限状态机 Math Preliminaries & Finate State Automata

数学初步（有些内容 CS172 学过了）

集合 sets

通常：小写字母代表元素，大写字母代表集合

$\mathbb{N}$，$\mathbb{Z}$，$\mathbb{Q}$，$\mathbb{R}$，分别表示自然数集、整数集、有理数集、实数集

这里（包括 Sipser 的教材）认为自然数集 $\mathbb{N}$ 是不包含 $0$ 的

$\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}$

$\mathbb{Q}^c$ 表示无理数集，$\mathbb{C}$ 表示复数集

$\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}^c$

集合运算

  • 并集，$A \cup B$
  • 交集，$A \cap B$
  • 取反，$\overline A$
  • 减法，$A \backslash B$
  • 德摩根律
  • $\overline{\overline A} = A$
  • $\overline{A \cup B} = \overline A \cap \overline B$
  • $\overline{A \cap B} = \overline A \cup \overline B$
  • 分配律
  • $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
  • $A \cup (B \cap C) = (A \cap B) \cup (A \cap C)$
  • 笛卡尔积，$A \times B$，也叫做叉积

函数 functions

函数是两个集合之间的二元关系。第一个集合当中的每个元素，最多与第二个集合当中的一个.有关（映射到）。

从集合 $A$ 到集合 $B$ 的函数 $f$，说白了就是定义域 $A$ 而值域是 $B$，可以表示为 $f: A \rightarrow B$，而这个函数是两个集合的笛卡尔积的子集，即：$f \subseteq (A \times B)$

若 $(a, b) \in f$ 则 $f(a) = b$，vice versa。

字符串 strings

字符串基础知识

  • 字母表（alphabet）：任意的非空有限集。通常用 $\Sigma$ 表示
  • 字母表当中的元素，称之为字母表的 符号（symbols）
  • 字母表上的字符串（a string over an alphabet）是该字母表上的符号的有穷序列，且不含逗号、空格等分隔符
  • 字符串的集合，称为 语言（language）
  • 字符串 $w$ 的长度表示为 $|w|$，长度为零的是空串，常用 $\epsilon$ 表示
  • 若字母表 $\Sigma$ 上的字符串 $w$ 的长度为 $n$，则可以写作 $w = w_1 w_2 \cdots w_n$ ，翻转 $w^R = w_n w_{n-1} \cdots w_1$
  • 原始串当中连续（consecutively）出现的一段字符，是子串（substring）

连接（concatenation）

  • 假设 $s$ 串的长度是 $n$，$t$ 串的长度是 $m$，则 $s$ 和 $t$ 的连接记作 $st$，$st = s_1 s_2 \cdots s_n t_1 t_2 \cdots t_n$

  • $w^k$ 表示 $k$ 个 $w$ 依次连接，即：$w^{k+1} = ww^k$，$w^0 = \epsilon$

字符串的偏序

  • 若 $x, y, z$ 是三个字符串且 $y = xz$，则 $x$ 是 $y$ 的 前缀（prefix），满足 $x \subseteq y$。

  • 特殊的，若 $z \not= \epsilon$，则 $x$ 是 $y$ 的 真前缀（proper prefix），此时满足 $x \subset y$。

  • 如果在一个语言中，任何一个成员都不是其他成员的真前缀，则这个语言是前缀无关的 （无前缀的）（prefix-free）

语言连接

与字符串的连接类似：

  • 若 $A$ 和 $B$ 是两个 语言（language），则定义 $A \cdot B = \{xy: x \in A, y \in B\}$ ，也可写作 $A \times B$

  • $A^{k+1} = A \cdot A^k$，$A^0 = \{\epsilon\}$。

克莱尼星号 Kleene Star

  • 这个星号是一种正则运算（连接）。$A^*$ 可以读作「A-Star」。
  • 若 $A$ 是一个语言，则定义 $A^=\bigcup_{k \geq 0} A^k$（Sipser 的教材写作 $A^ = \{x_1x_2 \cdots x_k | k \geq 0 \text{且每一个} x_i \in A\}$），表示 $A$ 中任意个字符串连接形成的新串们构成的新语言。所以，$\epsilon$ 也是 $A^*$ 的成员。
  • $A^*$ 当中有 $\infty$ 个字符串。
  • 除了 $A^$，还有一种东西叫做 $A^+$，说白了就是把 $\epsilon$ 从 $A^$ 当中删掉。这两种表示和正则表达式当中一致。
  • 字母表 $\Sigma$ 上的语言（language over an alphabet），都是 $\Sigma ^*$ 的子集。

有穷自动机和正则

有穷自动机是描述能力和资源 极其有限 的计算机的 模型，经常被用作各种机电设备的控制器，如自动门等。

马尔科夫链（Markov chain）是一种概率的计算模型，是有限自动机的概率对应物。常用于识别数据中的模式，甚至用于预测金融市场的价格变化。

定义

一个有穷自动机 $M$ 是一个五元组 $(Q, \Sigma, \delta, q_0, F)$：

  • $Q$ 是有限的状态集
  • $\Sigma$ 是有限的字母表符号的集合
  • $\delta$ 是转换函数，$\delta: Q \times \Sigma \rightarrow Q$
  • $q_0$ 是初始状态（state）
  • $F$ 是有限的接受态的集合（states）

若有一个有穷自动机 $M_1$ 接受的全部字符串，构成集合 $A$，即 $A$ 是 $M_1$ 接受的全部字符串集合，则称：

  • $A$ 是 $M_1$ 的语言（$A$ is the language of $M_1$）
  • $M_1$ 识别 $A$（接受了语言当中的所有字符串，即识别该语言）
  • $A = L(M_1)$

因此，一个自动机可以接受许多字符串，但永远只能 识别（recognize） 一个语言。

正则语言

正则（regular） 语言是指，存在某个有穷状态机，可以识别它。

例子：字母表 $\{0,1\}$ 上有三个语言 $A,B,C$，

  • 语言 A：包含子串 11（正则）

  • 语言 B：1 的个数是偶数（正则）

  • 语言 C：0 与 1 的数量相等（非正则）（上下文无关）

正则运算

设 $A$ 和 $B$ 是两个语言，则定义以下三个正则运算：

  • 并（union）：$A \cup B = \{w \mid w \in A \text { or } w \in B\}$
  • 连接（concatenation）：$A \circ B = \{x y \mid x \in A \text { and } y \in B\}=A B$
  • 星号（star）：$A^* = \left\{x_1 \ldots x_k \mid \text { each } x_i \in A \text { for } k \geq 0\right\}$

正则表达式就是由以上三种正则运算和 $\Sigma, \emptyset, \epsilon$（atomic）构建出来的。（这条表述可能不太严谨，理解意思就好）

封闭性（closure）

正则语言类在三种正则运算下封闭。

正则语言类在 union 运算下封闭

若 $A_1, A_2$ 都是正则语言，则 $A_1 \cup A_2$ 也是正则语言。

证明：

若自动机 $M_1 = (Q_1, \Sigma, \delta_1, q_1, F_1), M_2 = (Q_2, \Sigma, \delta_2, q_2, F_2)$ 分别识别 $A_1, A_2$，则构造 $M = (Q, \Sigma, \delta, q_0, F)$，把 $M_1$ 和 $M_2$ 的所有状态做笛卡尔积（相当于同时记录两边的路径）扔给 $M_3$ 即可。即：

  • $Q = Q_1 \times Q_2$
  • $q_0 = (q_1, q_2)$
  • $\delta((q, r), a) = (\delta_1(q, a), \delta_2(r, a))$
  • $F = (F_1 \times Q_2) \cup (Q_1 \times F_2)$，意思是第一个的接受态配上第二个的任意状态，并起来第二个的接受态配第一个的任意状态。这个表达式也可以改写为 $F = \{(q, r) | q \in F_1 \text{或} r \in F_2\}$
  • 注意 $F \not= F_1 \times F_2$，这种表示方法是交集，因为 pair 中的两个元素必须分别在 $F_1, F_2$ 当中，才能积进 $F$。
  • $F = F_1 \cup F_2$ 的写法也不准确。因为直接并起来，元素都是单独的，没有 pair 到一起。

总而言之，就是升高了一维，变成了二维。

图示见 Slide 2 的第 10 页。

对应的 NFA：

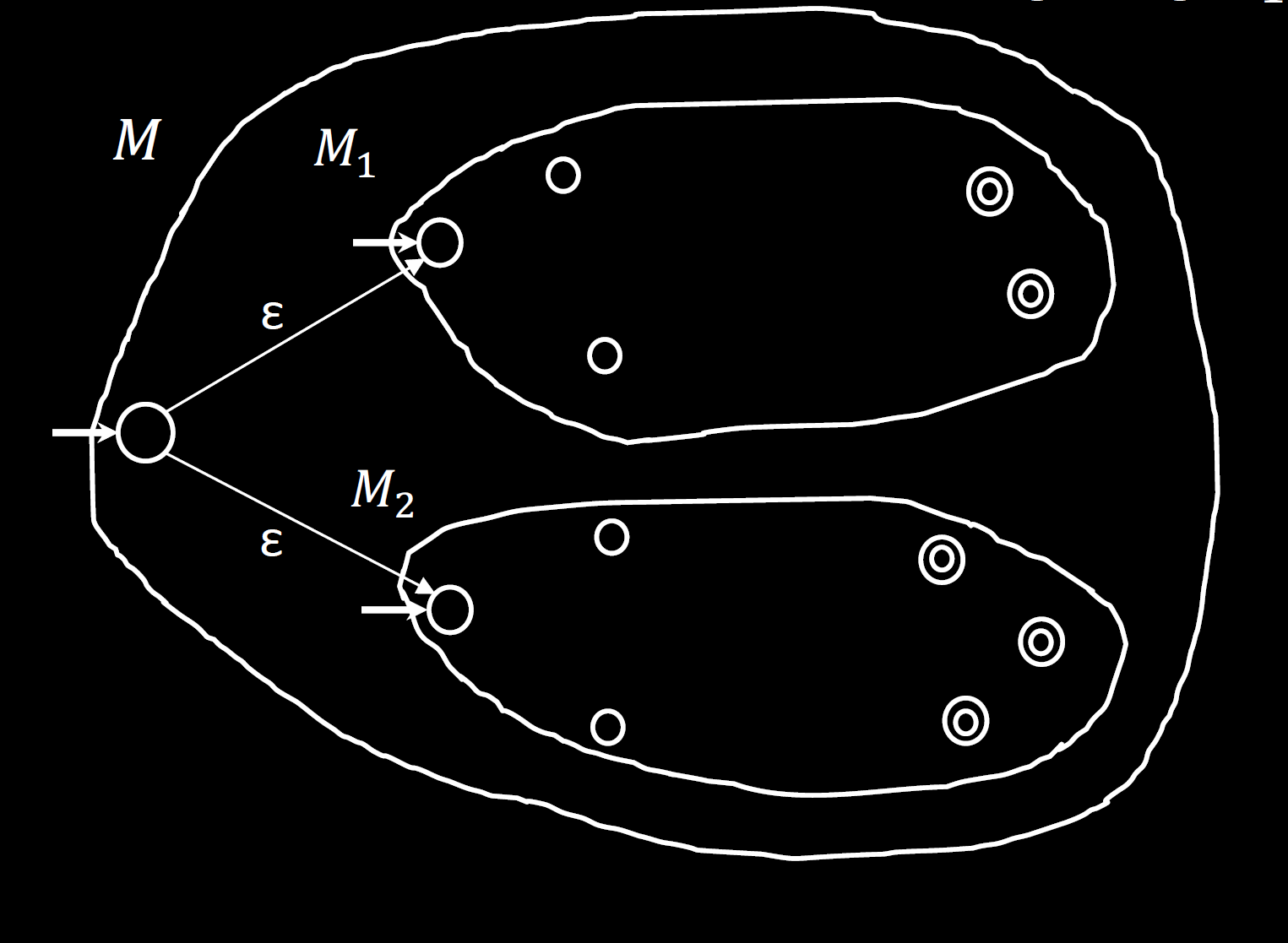
image-20220915230346059

正则语言类在 concatenate 运算下封闭

若 $A_1, A_2$ 都是正则语言，则 $A_1 \circ A_2$ 也是正则语言。

证明：

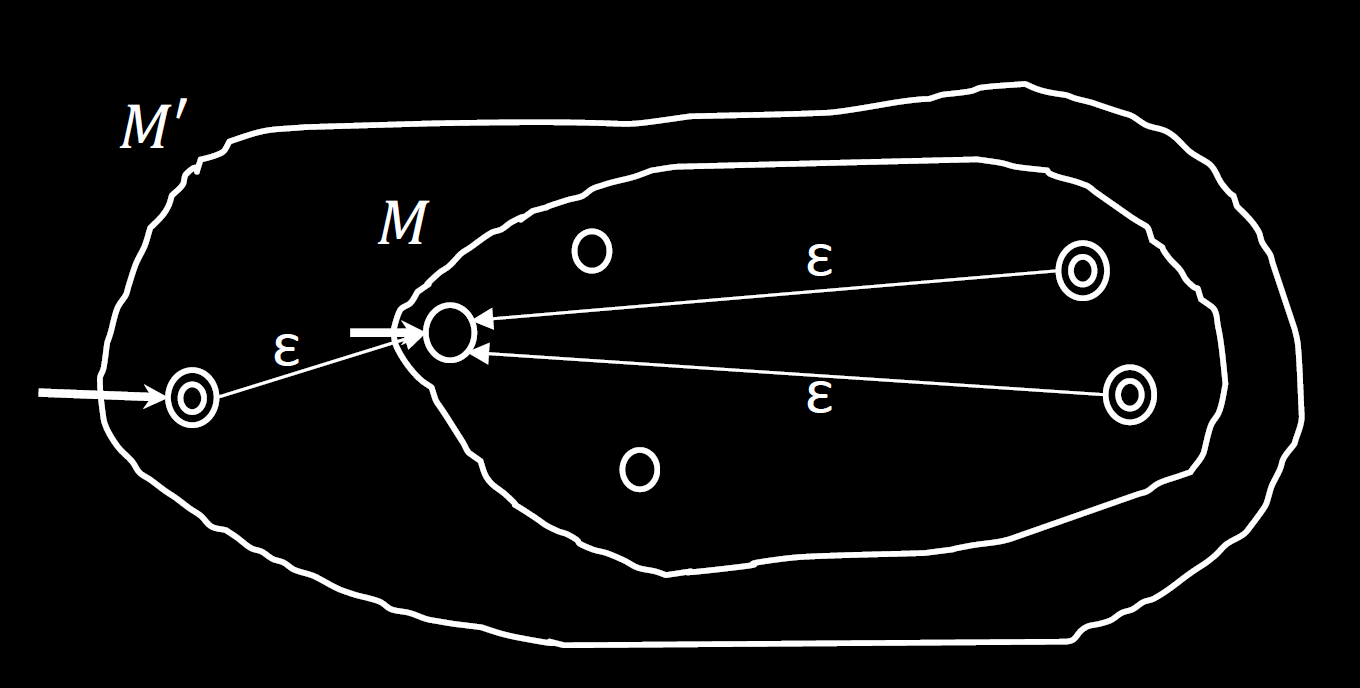
若 NFA $N_1, N_2$ 分别识别 $A_1, A_2$，则构造 $N$，把 $N_1$ 的接受态连边到 $N_2$ 的初始状态即可，边权是 $\epsilon$。然后把原先的接受态改为普通状态。

图示见 slide1 的第 38 页（Slide 2 的第 11 页）

对应的 NFA：

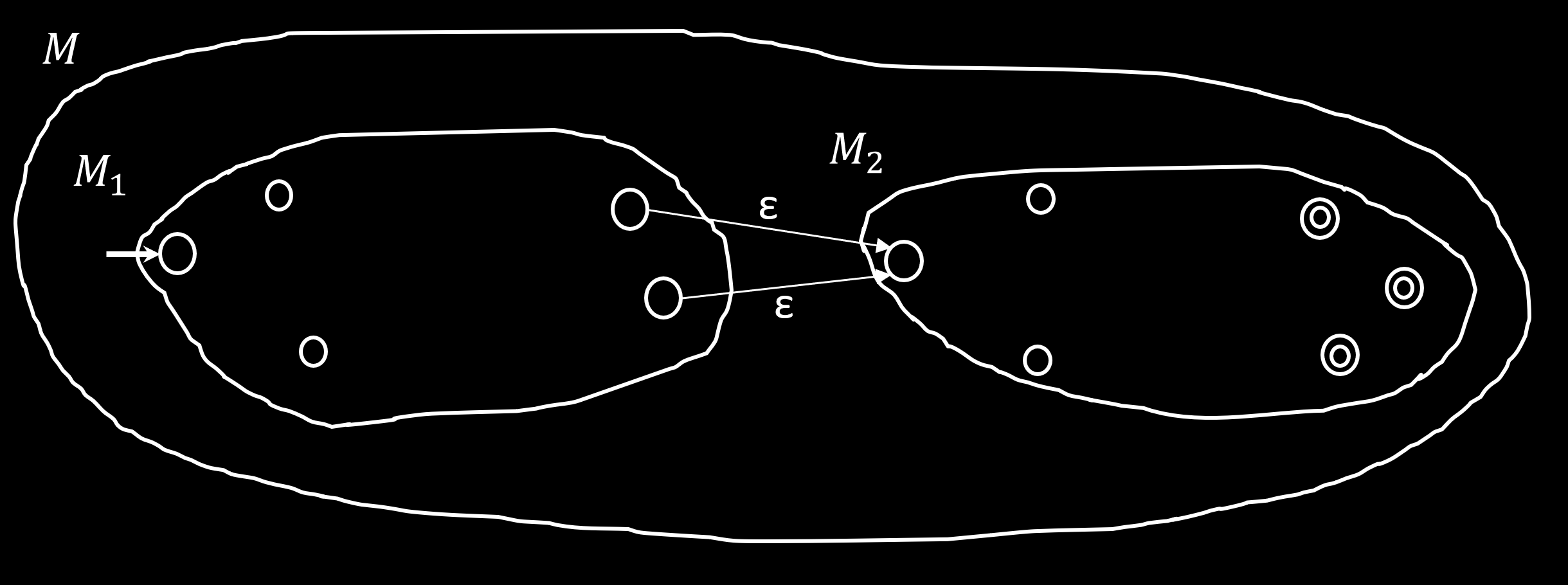
image-20221124195046035

正则语言类在 star 运算下封闭

若 $A$ 是正则语言，则 $A ^ *$ 也是正则语言。

对应的 NFA：（注意空的时候也可以接受）

image-20220915230354918