Lecture 10. Path Coverage 路径覆盖（旷课了）

先考虑不包含循环的情况（只有条件判断）。

就是对于 CFG，要从 起始节点（source node） 到 终止节点（sink node） 的所有可能路径，都跑一遍。

也就是说，每一个 testcase，都是一个路径。每一个测试数据，也只包含一个测试点（路径）。然后设计能走这个路径的测试数据就好了。

包含循环的 CFG

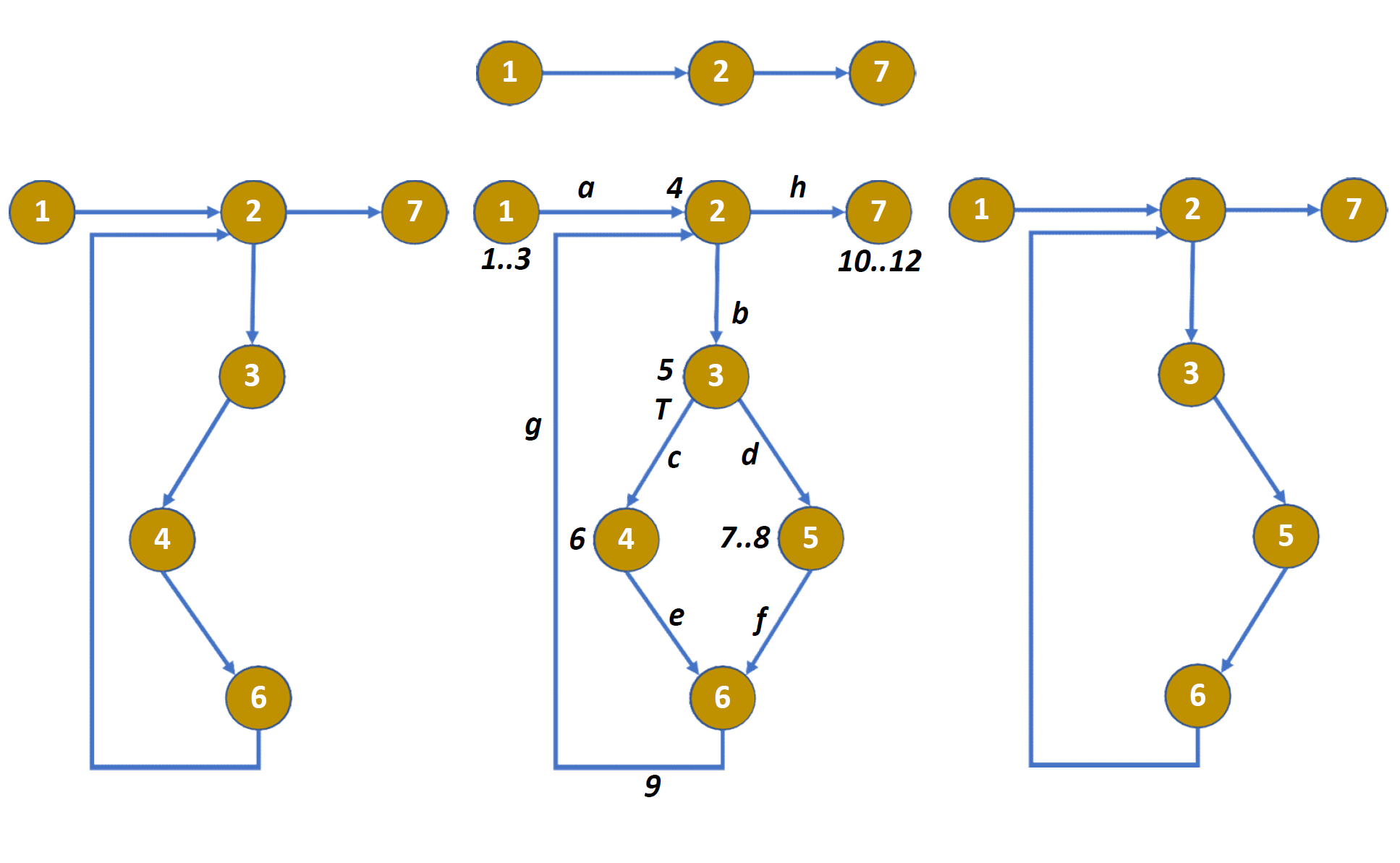
对于包含循环的 CFG，只需要考虑两种路径：一次循环都没执行的路径、执行 $n(n>1)$ 次循环的路径。也可以差不多理解成执行零次和执行一次。比如下图中间那个 CFG，可以拆成三条路（一条是不执行循环的，另外两条执行循环的）

与正则表达式结合

控制流可以用正则表达式表达。

正则表达式三种运算

连接（concatenation，.），就是一个点，表示控制流图当中的一个节点（一段连续的代码）
选择（selection，+），就是一个加号，表示控制流图当中做一个决定
迭代（iteration，()*），就是一个括号外面套个星号，表示控制流图当中一段重复的

比如，上面那个 CFG，就可以用正则表达式描述成：1.2.(3.(4+5).6.2)*.7。

由于由于可以把循环当作只执行一次或者不执行，于是这个循环就退化成了一个简单的条件选择语句。用 0 表示什么都不执行，那么 ()* 就可以用 (()+0) 代替，于是刚才的正则表达式可以化简成：1.2.((3.(4+5).6.2)+0).7。

用正则表达式计算路径总数

神奇的地方来了。把化简后的正则表达式当中的 + 当成加号 $+$，. 当成乘号 $\times$，再把所有节点编号（包括 0）都当成数字 $1$，括号保留不变，然后直接计算这个表达式的值，就是路径总数了。

比如刚才那个正则表达式代表的路径总数就是：$1 \times 1 \times ((1 \times (1 + 1) \times 1 \times 1) + 1) \times 1 = 3$。

从正则表达式当中提取路所有路径

还是要看简化后的正则表达式 1.2.((3.(4+5).6.2)+0).7。

对于表达式当中的每一个这种形式 pre.(x+y).suf，把加号 + 左右两边的东西提出来，拆成俩：pre.x.suf 和 pre.y.suf。比如上面那个正则，就可以拆成 1.2.3.（4+5）.6.2.7 和 1.2.0.7。左边那个由于还是 pre.(x+y).suf 的形式，所以还可以继续拆成 1.2.3.4.6.2.7 和 1.2.3.5.6.2.7。右边那个，由于 0 相当于啥都没执行，所以最后可以删去，变成 1.2.7。

于是，这一个正则表达式可以提取出来三条不同的路径：1.2.3.4.6.2.7、1.2.3.5.6.2.7、1.2.7。跟之前计算出来的路径总数（三条）一致。

还有一个稍微复杂一点的例子。

正则表达式（化简后）是：1.(2+0).3.(4+(5.(6+0))).7，路径提取过程是，先把 pre.(2+0).suf 拆成如下的俩：

1.2.3.(4+(5.(6+0))).7，然后这个拆出俩：1.2.3.4.7 和 1.2.3.5.(6+0).7
后面那个又拆成俩：1.2.3.5.6.7 和 1.2.3.5.7
1.3.(4+(5.(6+0))).7，然后这个拆出俩：1.3.4.7 和 1.3.5.(6+0).7
后面那个又拆成俩：1.3.5.6.7 和 1.3.5.7

总计六个路径。

小结

路径覆盖没有去考虑每一个条件或者判定的取值，但是可以覆盖到所有的可能的组合产生的路径。

如果程序比较复杂，那么很难找出所有的路径。就算找出来了，测试的时候也要花好多时间。