Chapter 3 Part 3: 算术运算

（共 49 页）

二进制整数乘法（无符号）

$A \times B$，先不考虑交换律，把 $A$ 称作 multiplicand（被乘数），把 $B$ 称作 multiplier（乘数）。对于乘数的每一位（$i \in [0, w-1]$）分别考虑：

若第 $i$ 位是 $1$，答案就加上 $A$ 左移 $i$ 位
若第 $i$ 位是 $0$，答案不变

相当于列竖式计算。

事实上，把答案右移保留尾位、再把 $A$ 加给答案的最高位，得到结果也是一样的，但是比较麻烦。

硬件二进制整数乘法（无符号）

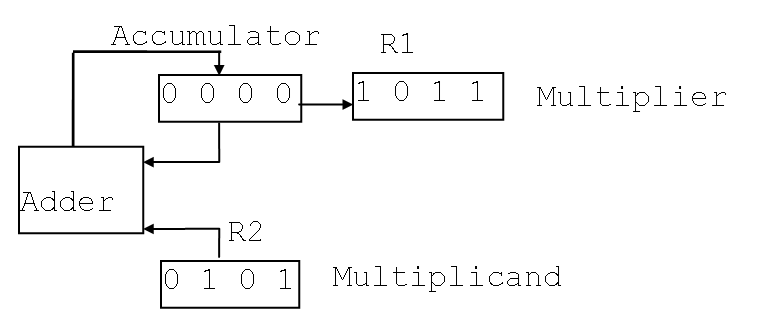
实现 $4$ 位二进制乘法的硬件组合如图所示。将累加器 $Acc$ 和寄存器 $R_1$ 串联起来，得到了一个八位右移寄存器。由于两个 $4$ 位二进制数相乘，得到的结果最大就是 $8$ 位二进制，所以这个八位右移寄存器可以用于存储答案。此外，存在一个加法器 $Adder$，以 $Acc$ 和 $R_2$ 作为输入，再把输出（加法结果）传送给 $Acc$。

运算过程是：

$Acc$ 初值赋零。$R_2$ 赋初值为被乘数，$R_1$ 赋为乘数。
如果 $R_1$ 的最低位是 $1$，就把 $R_2$ 和 $Acc$ 做一次加法，结果存储给 $Acc$。
八位寄存器 $[Acc, R_1]$ 整体右移。
第二、三步，重复 $4$ 次。
最终，八位寄存器整体的值就是答案。用（伪）程序语言来描述就是：

uint8_t mul(uint4_t R_1, uint4_t R_2) {
  // R_2 * R_1
  uint4_t Acc = 0;
  for (int i = 0; i < 4; ++i) {
    if (R_1 & 1) Acc += R_2;
    R_1 >>= 1;
    R_1 += (Acc & 1) << (4 - 1);
    Acc >>= 1;
  }
  return (Acc << 4) + R_1;
}

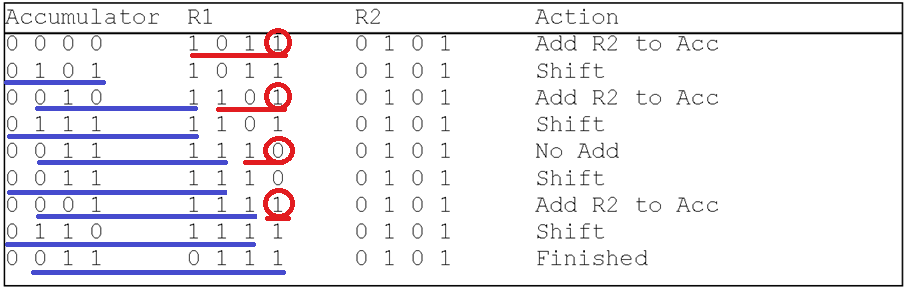
下图逐步描述了 $1011 + 0101$ 的硬件级运算过程。

有符号怎么办？

课件上没有说直接当成补码运算是否可行。但是说，可以把符号去掉，运算完之后再加上符号。

二进制整数除法（无符号）

依然是列竖式。但是除法的竖式计算比较麻烦。

暂时用 $\div$ 表示整数除法。设 $A \div B = C \dots D$，称：$A$ 是 dividend（被除数），$B$ 是 divisor（除数），$C$ 是 quotient（商），$D$ 是 reminder（余数）。

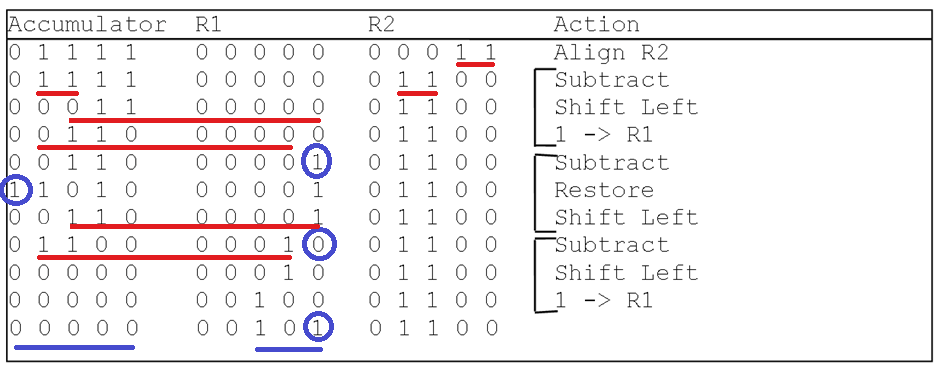
硬件二进制整数除法（无符号）

结构类似于硬件二进制整数乘法。

注意，对于 $w$ 位二进制无符号整数除法，需要使用三个 $w+1$ 位的寄存器，这一点与只需要 $w$ 位寄存器的乘法有区别。因为需要用额外的一个 bit 来表示执行减法后是否会导致结果小于零（我们还没学如何比较两个二进制数的大小。如果 $A-B<0$ 就表示 $A<B$，而有符号加减法可以直接用补码实现。如果相减得到结果小于零，就撤销这次减法操作，往后一位重新尝试减法）。这里的硬件与乘法还有一点不同，乘法是 $[Acc, R_1]$ 整体右移，除法是 $[Acc, R_1]$ 整体左移。

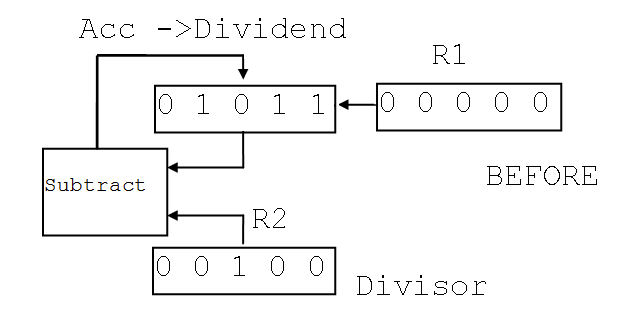
当被除数 $\geq$ 除数，则执行运算过程：

$Acc$ 赋初值为被除数 dividend。$R_2$ 赋值为除数，$R_1$ 赋值为零。
把 $R_2$ 的最高位与 $Acc$ 对齐（仅需第一次减法前进行一次对齐）
从 $Acc$ 中减去 $R_2$
若 $Acc < 0$
把 $R_2$ 加回去 $Acc$（撤销减法）
把 $[Acc, R_1]$ 整体左移，右侧补零
若 $Acc \geq 0$
把 $[Acc, R_1]$ 整体左移，右侧补一
重复数次上述过程（3，4，5）。~~重复几次，没看懂~~
最终 $Acc$ 中存储的是余数（~~可能还需右移几次，没看懂~~），而答案（商）存储在 $R_1$ 中。

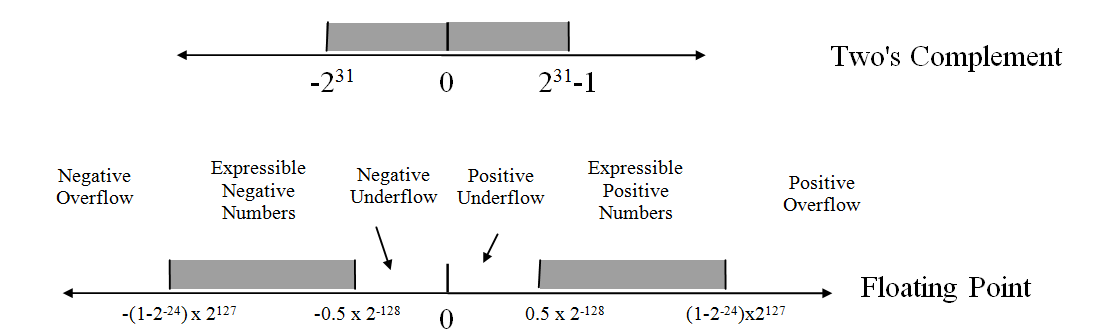
浮点数

25 页开始

IEEE 754

对于 32 位浮点数（正），表示的范围是：$2^{-149} \sim (1-2^{-23}) \times 2^{126}$。咋算出来的不是很懂。数学真奇妙。