Chapter 3 Part 2: 触发器的应用以及时序逻辑电路设计

（共 47 页）

触发器在电路中的几个应用

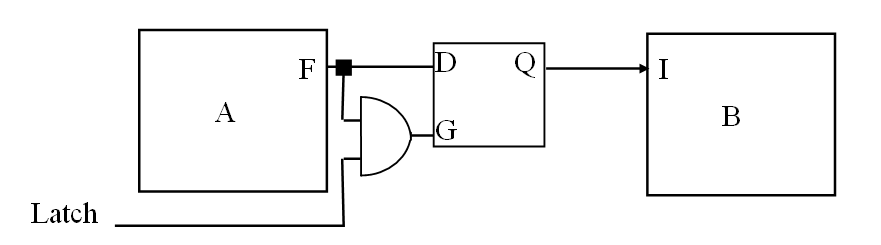
应用一：数据锁存 data latching

假设两个电路 A 和 B。此时 A 计算出了某个值，想要传给 B，但是 B 要过一会儿才有功夫接收。在这段等待时间里，A 还想要做点别的事情。于是 A 可以把数据送给一个 D 触发器存起来，然后干别的事情去，B 有功夫了再从 D 触发器里面取走数据。

应用二：寄存器（移位寄存器）

大概对应维基百科上面的 hardware register 页面：https://en.wikipedia.org/wiki/Hardware_register

寄存器是由一组触发器连接而成的一个单元。寄存器上的每一个触发器都能处理一位的信息。寄存器有许多种类型，比如移位寄存器（shift register），就能实现相邻触发器之间的数据传送，即按位移动。

比如这个电路（俩主从 JK 触发器构成，也就是其实总共有四个触发器）就实现了一次按位移动。（注意 $K$ 相当于 Reset，$J$ 相当于 Set，$K$ 真则 $Q$ 假 $Q'$ 真，$J$ 真则 $Q$ 真 $Q'$ 假，也就是 $J$ 的值会传给 $Q$，$K$ 的值会传给 $Q'$，再分别传给下一个的 $J/K$。

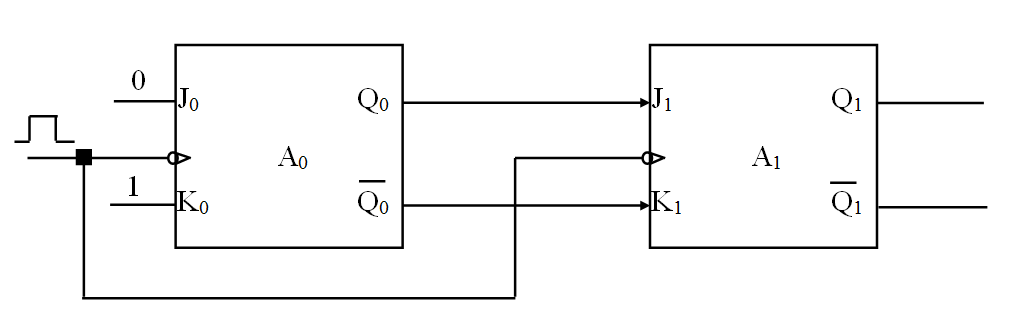
数据向左向右的 shift，分别相当于一个二进制数的乘以二、除以二操作。

~~讲道理，移位寄存器，用 D 触发器实现感觉更简单，不懂这里为啥要用 JK~~

应用三：异步计数器（Asynchronous Counter）

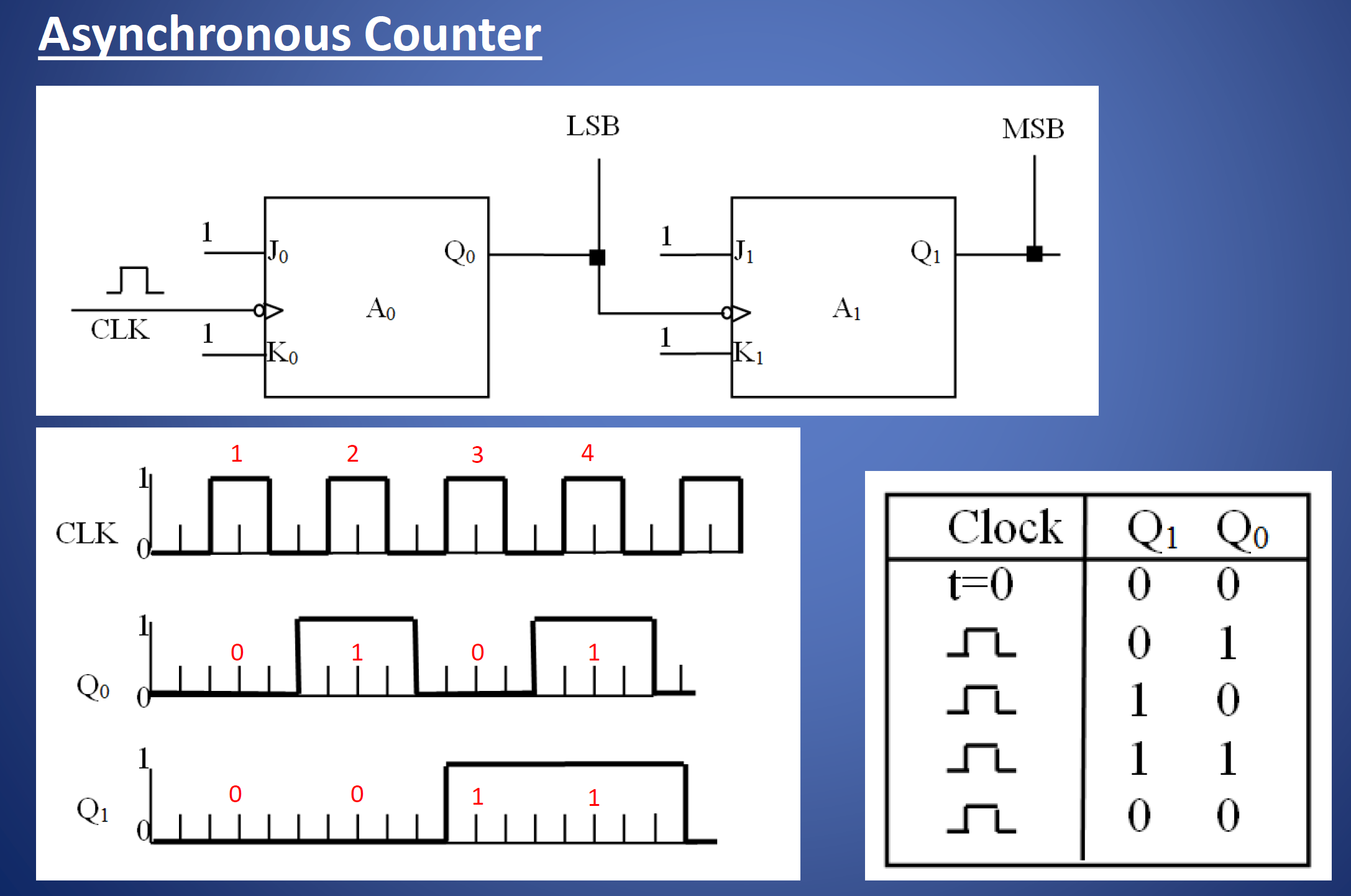
如图。两个脉冲触发的（主从） JK 触发器，第一个表示第零位，第二个表示第一位。所有 JK 的输入都永远为 1（别忘了，JK 触发器当 $J=K=1$ 时，作用是翻转输出值）。第一位的输出信号作为第二个的时钟信号。$Q_1$ 的频率是 $Q_2$ 的一半，在二进制数字上，体现为高位的变化频率等于低位的一半。

横轴每个小格代表 $\Delta t$，这里假设 $\Delta t$ 是一整个触发器的延迟（而不是一个 gate 的延迟）。由此可见，对于异步计数器，每个 JK 触发器可以处理一位。整体的延迟会随着位数的增加而增加。如果是 32 位，那么就会有 $32 \Delta t$ 的延迟。这个延迟太高了，无法接受。

延迟可能造成极端的情况：四位异步计数器，假如当前状态是 $1111$，那么下一个状态应当是 $0000$。但是进入这个状态之前，由于延迟巨大，可能会经历 $1110, 1100, 1000$ 三个中间状态。假如这个四位计数器用到大型电路里面去，这几个中间状态就可能会导致严重的 internal error。为了解决这个问题，需要考虑同步（Synchronous）计数器。

应用四：同步计数器（Synchronous Counter）

~~这里的同步/异步计数器好像跟国内教材的不太一样？~~

同步计数器是同步电路的一种。同步电路是指，所有触发器的时钟信号都是来自于一个共同的时钟源。不像异步计数器，每个触发器的时钟信号都来自上一个的输出。

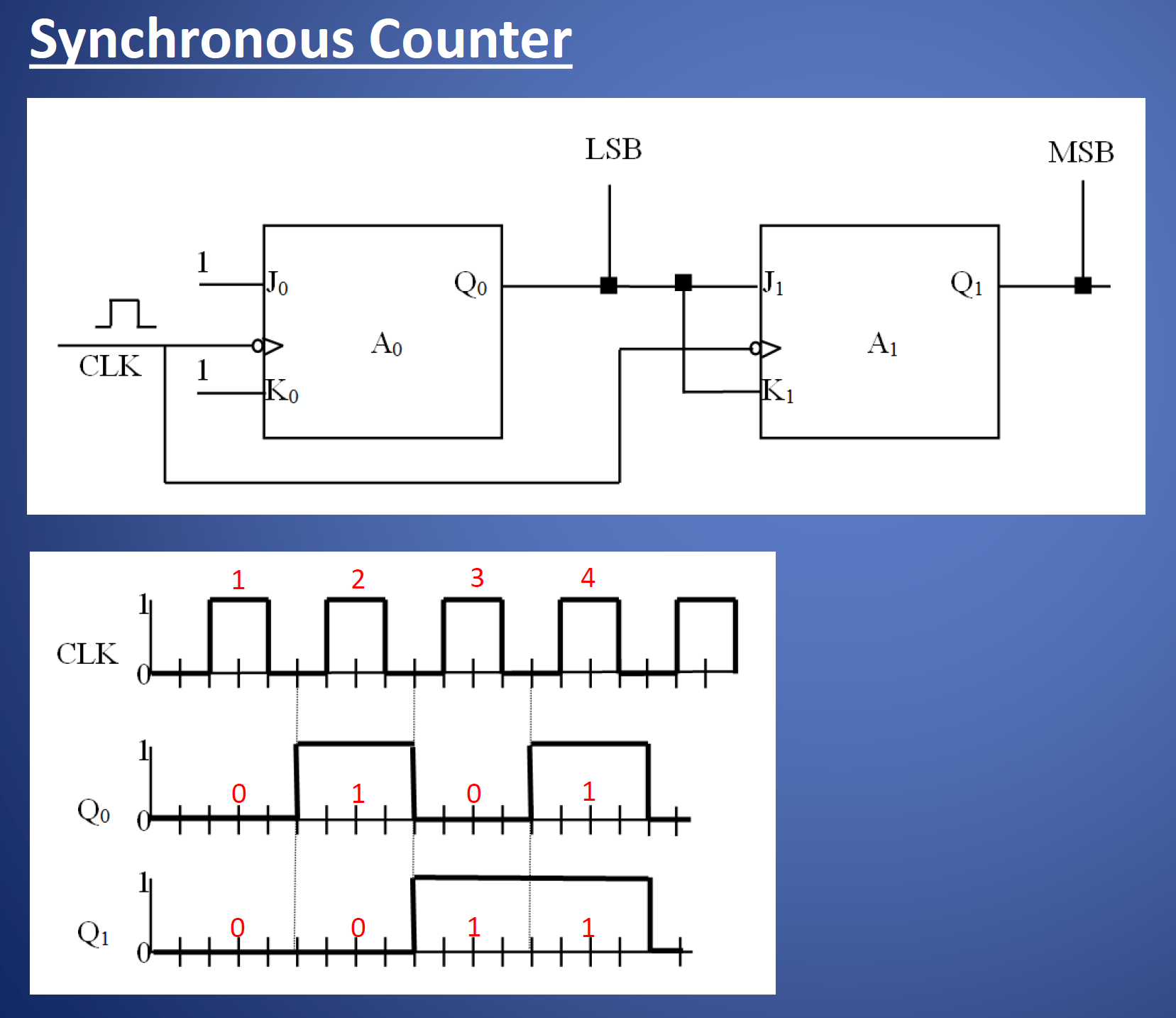
像这样设计的同步计数器，CLK 信号连接到了两个触发器的时钟输入端。因此，$Q_0$ 和 $Q_1$ 总是同步的。更进一步，无论是多少位的计数器，每个输出都是同步的，延迟都是仅有一个 $\Delta t$，时间复杂度 $O(1)$。

异步计数器的 JK 永远为 1，在同步计数器当中，$J = K = Q_{\text{last}}$，同样，利用了 $J=K=1$ 翻转输出的性质。

应用五：多功能寄存器（Multipurpose Register）

场景：你需要完成多次操作。每次操作是两种类型之一：

LS，需要实现一个 2 位左移寄存器
CNT，需要实现一个模 4 计数器

首先，将两种功能分开，讨论单独的电路情况。

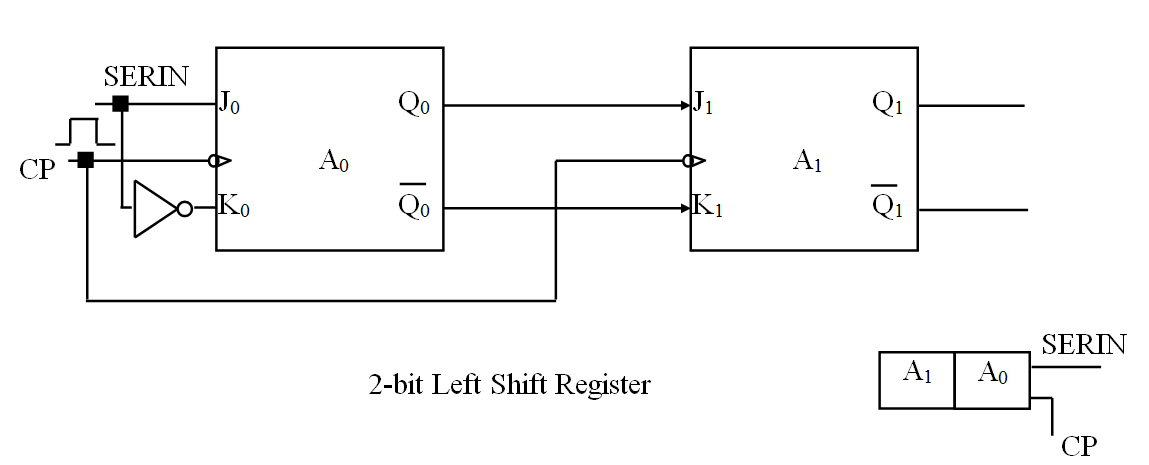
此时，$Ls = 1$，$J_0 = Serin$，$K_0 = Serin'$，$J_1 = Q_0$，$K_1 = Q_0'$。

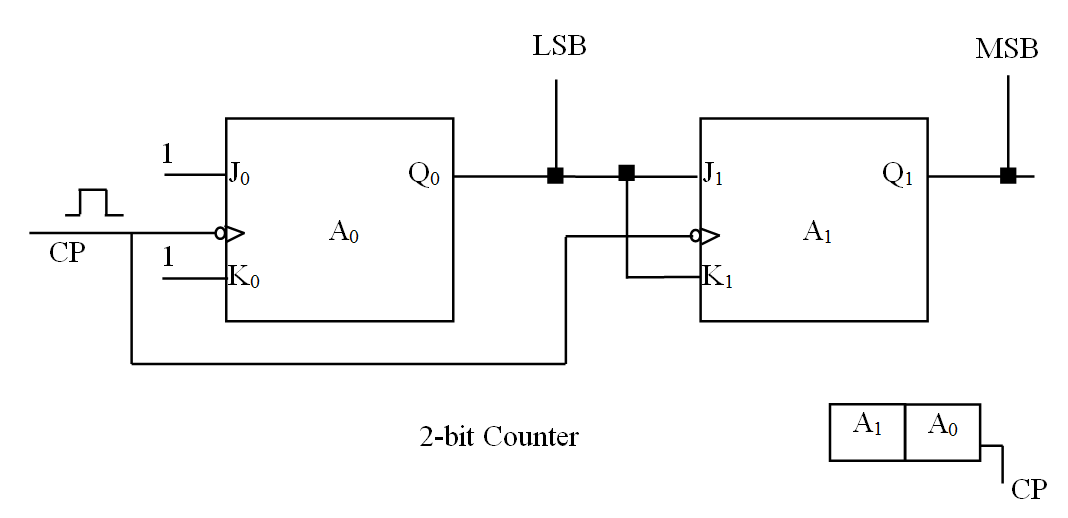
此时，$Cnt = 1$，$J_0 = K_0 = 1, J_1 = K_1 = Q_0$。

结合一下两个情况，利用 SOP，得出以下式子：

$J_0 = Cnt + Ls \cdot Serin$
$K_0 = Cnt + Ls \cdot Serin'$
$J_1 = Cnt \cdot Q_0 + Ls \cdot Q_0$
$K_1 = Cnt \cdot Q_0 + Ls \cdot Q_0'$

于是就可以把这俩东西的电路合在一起了。

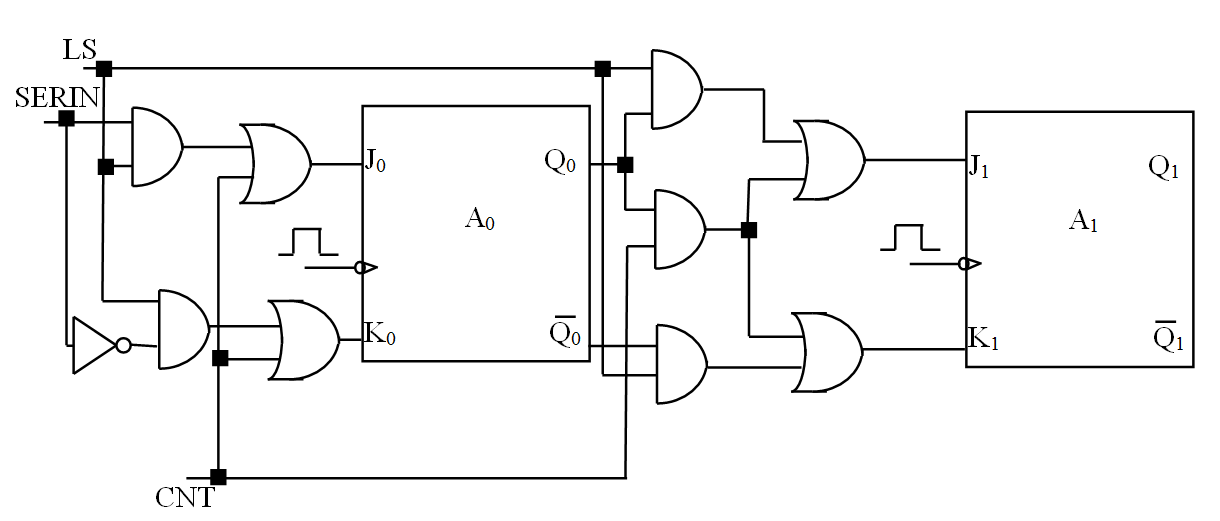
然而，这种设计方法非常令人大跌眼镜，简直是乱搞嘛，根本不具有普遍适用性。

时序电路设计

课件以一个电路作为示例，描述如何设计时序电路。

状态图和状态表

通常，设计时序电路的时候，都是先画出状态图（state diagram）~~感觉有点像 DFA~~，然后推导出状态表（state table）。通常，电路的输出也会包含在状态图里面。

比如这张状态图，是一个 状态/输出表（state/output table），对应这样一个电路：

$Z$ 是 电平输出 level output，当遇到奇数个 $1$ 的时候 $Z=1$，否则 $Z=0$
$z$ 是 脉冲输出 pulse output，当遇到偶数个 $1$ 的时候 $z=1$，否则 $z=0$

注意，这里的脉冲输出，并不是只其值由一段脉冲输入决定，而是他本身是一个脉冲。也就是最重要在输出的时候，与时钟做一个 AND。电平输出的值也可以由一段脉冲决定。

斜杠 slash 前面的 $1, 2$ 代表状态的编号，斜杠后面的 $Z=0$ 或者 $Z = 1$ 代表变量 $Z$ 的输出值。

~~这个脉冲输出的箭头方向，看起来很怪？~~

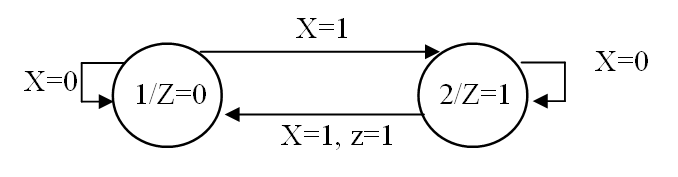
等价状态

有时候，根据电路的 规格要求（specification） 设计出来的状态表，会有冗余（redundant）的状态，冗余的状态就会让电路变得复杂。比如，若两个电路状态在相同的输入下有相同的输出，并且转移到同样的一个次态去，则称这两个状态是 等价状态（equivalence states）。（假如输出相同，但是转移不同，不视为等价状态。）显然可以通过重新设计状态图等方法，去重、精简。

假设一个电路有 $M$ 个状态，需要 $n$ 个触发器来实现这个电路，那么 $n$ 的取值必须满足 $2^{n-1} < M \leq 2^n$。

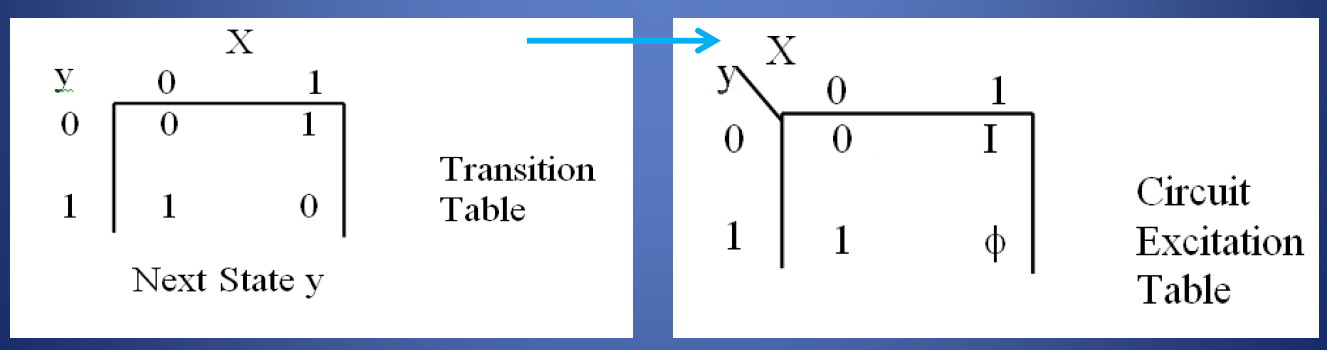
转移表 transition table

上面的电路，一共有两个状态，所以可以用一个触发器来实现。令触发器的输出值 $y=0$ 代表状态 $1$，$y=1$ 代表状态 $2$

下图当中，左边是状态表（同时包含输出），右边是转移表。转移表描述了触发器的行为。

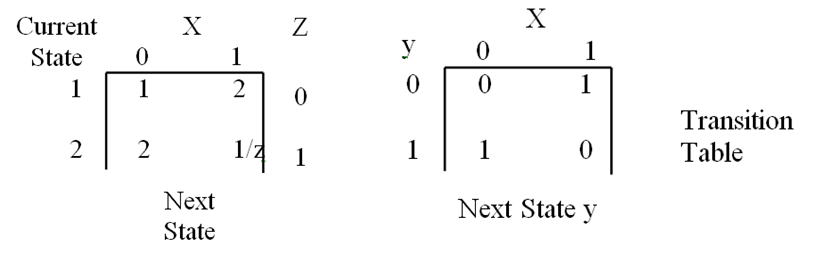
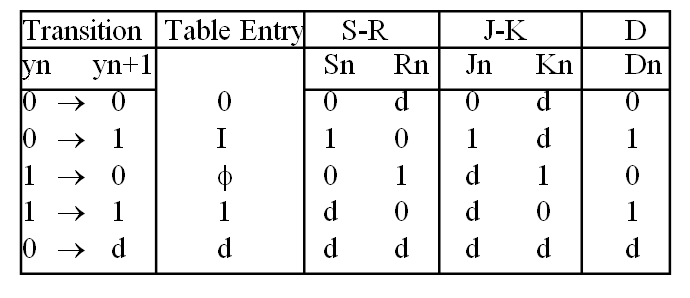
激励表 excitation table

定义几个符号：

$I$ 表示 $0 \rightarrow 1$ 的转移
$\Phi$ 表示 $1 \rightarrow 0$ 的转移
$1$ 表示维持 $1$ 状态（$1 \rightarrow 1$）
$0$ 表示维持 $0$ 状态（$0 \rightarrow 0$）
$d$ 表示上面四种随便转移，don't care

这张图表示，如果想要实现左边的转移，触发器的输入值应该如何选择。

有了激励表，就可以把电路的转移表替换掉。因为用上面这四种符号，比只有 $0,1$ 看起来要明了很多。

激励方程 excitation equation

激励方程，用于描述触发器输入端的取值。比如 JK 触发器，就要用俩方程，一个描述 $J$ 等于啥，另一个描述 $K$ 等于啥。

依然以 JK 触发器为例。$J$ 和 $K$ 有 $0, I, \Phi, 1$ 四个值。

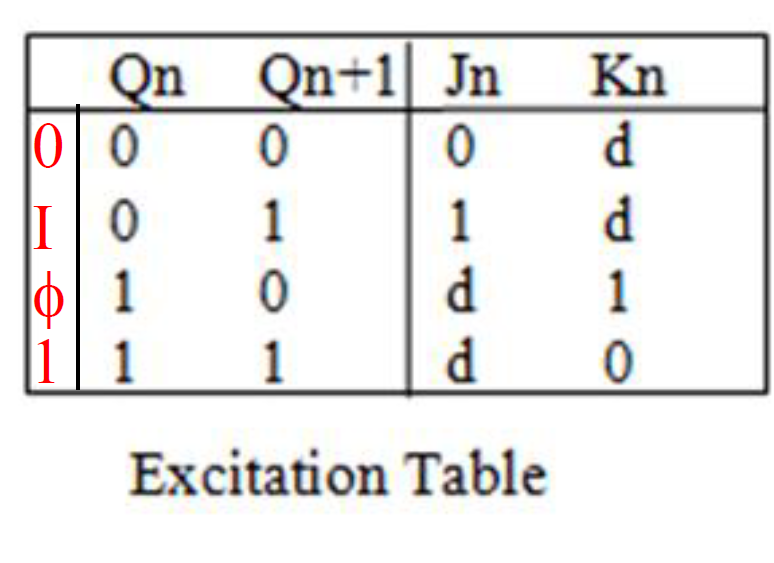
对于 $J$，$I=1,0=0,\Phi=1=d$，意味着，$J$ 的卡诺图当中，$I$ 必须圈，$0$ 必须空着，$\Phi$ 和 $1$ 圈不圈都行
对于 $K$，$\Phi=1, 1 = 0, 0 = I = d$，意味着，$K$ 的卡诺图当中，$\Phi$ 必须圈，$1$ 必须空着，$0$ 和 $I$ 圈不圈都行

于是 $J$ 和 $K$ 都可以这么圈圈。

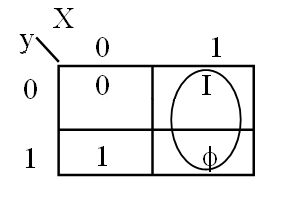
那么，$J = X$ 和 $K=X$ 就是这个触发器的激励方程。

输出方程 output equation

根据以上设计，易得：

$Z = y$
$z = X \cdot y \cdot ClockPulse$（$X \cdot y$ 表示遇到偶数个 $1$，而 $z$ 又是一个脉冲输出）

最终，电路就设计完了

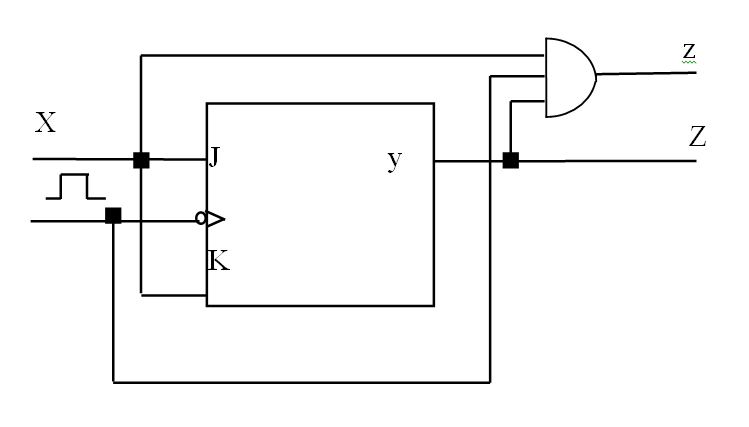
步骤总结

构造状态图
根据状态图写出状态/输出表
如果有等价状态，化简一下，要去重
secondary state assignment，也就是确定用多少个触发器，每个触发器代表什么状态之类的
推导转移表（针对触发器）
推导电路的激励表
根据激励表，选择合适的触发器类型，并结合卡诺图，推导激励方程
推导输出方程
画出逻辑电路图