Chapter 3 Part 1: 触发器 flip flop

（共 46 页）

时序逻辑设计（引言）

众所周知，数字逻辑主要分为两大类，一个是 组合逻辑（Combinational Logic），另一个是 时序逻辑（Sequential Logic）。

组合逻辑电路就像是实现了一个简单的布尔函数。组合逻辑电路的输出值，完全取决于输入的值。当输入值发生改变，输出值也会立刻改变（如果忽略掉延迟的话）。

时序逻辑电路就不一样了。通常时序逻辑电路会包含 触发器（flip flop）。时序逻辑电路的输出与时间有关，是由输入值和当前状态共同决定的。

时序逻辑电路由时钟信号触发。若没有时钟信号，那么无论输入值如何变化，电路中的触发器都会保持当前的状态。

触发器是时序逻辑电路的基本组成部分。不同类型的触发器也具有不同的触发行为和输入组合。

SR 锁存器（Set Reset Latch）（NAND 实现）

SR 锁存器，是基本 RS 触发器的别称。

原理

接下来假设每一个门的延迟都是 $\Delta t$。

首先考虑这样的一个电路图

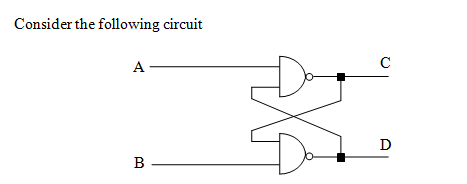
假如初始状态下，全都是零；先后把 $A, B$ 的两个输入值都拨到 $A = 1$ 且 $B = 1$ 的状态，那么输出就会是：$C = 0$，$D = 1$。不难发现，只要输入的值不再改变，那么两个输出的值就永远也不会变化。

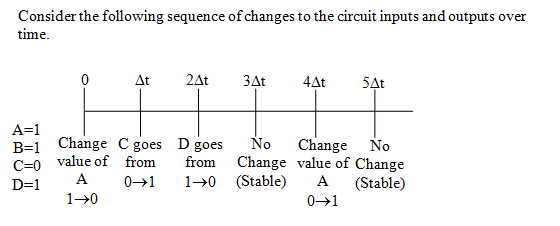
但是假如更改一下输入的值（此处拨动 A 开关），那么这个电路的输出就会发生一点变化。一个单位时间的延迟后 $C$ 的输出改变，两个单位延迟后 $D$ 的输出也改变，然后达到稳定状态（stable）。

然而就算这时候再把 A 重新拨为 1，输出的值依然是不会改变的，依然处于稳定状态（模拟一下这个电路的过程就明白了）。

换句话说，在计时器开始之前，以及 $5\Delta t$ 时刻，输入的值都是一样的（$AB = 1$），然而这两个时刻的输出不同。所以称这个电路是 双稳态（bistable） 的。

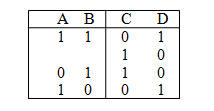
总结的讲，如果此时此刻，$A,B = 1,1$，那么这个电路其实是能「回忆起」上一个为零的输入是哪一个。假如 $C,D = 1,0$，就说明刚才 $A$ 是 0；反过来，假如 $C,D = 0,1$，那么上一个是 0 的输入就是 $B$。当然，如果此时此刻 $AB \not= 1$，输出就直接表示当前那个输入为零：状态表如下

那么假如 $A,B = 0,0$ 会怎么样？

$A, B = 0, 0$ 的时候，会输出 $C,D = 1, 1$。此时如果再同时把 $A$ 和 $B$ 改成 1，那么两个 NAND 门的四个输入就都是 1，从而 $C$ 和 $D$ 同时变为 0。接下来有趣的事情发生了：NAND 门不断地循环输出 0 和 1，即这一时刻输出俩 0，下一时刻输出俩 1，再下一时刻又变成了俩 0，如此往复…

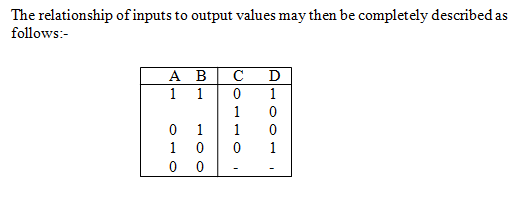
为了方便起见，不如干脆定义：这个电路不允许 $A,B = 0,0$ 的输入。于是状态表变成了这个样子：

改造

观察发现，$C$ 和 $D$ 的值永远是互补的。因此不妨用字母 $Q$ 代替 $C$，那么 $Q'$ 就表示 $D$。

观察还发现，当 $A,B$ 的取值变成 $1,1$ 的时候，电路的输出不会发生变化；然而直觉上好像 $A,B = 0,0$ 的时候电路不变更正常一些。因此以可以在输入端给 $A$ 和 $B$ 分别接上俩 NOT 门（不过这样就增加了一个单位延迟）。同时，$A$ 改名 $S$，表示 set；$B$ 改名 $R$，表示 reset。

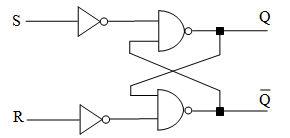
那么：

$S, R = 1, 0$ 的时候，经过 NOT 门之后对应刚才真值表的 $A, B = 0,1$，此时结果是 $Q = 1$，即设一（set）。
$S, R = 0, 1$ 的时候，结果是 $Q = 0$，即清零（reset）
$S, R = 0,0$，电路输出没有变化，即保持上一个输入的输出值
$S, R = 1, 1$，不允许这样的输入

同时可以推导出 $Q$ 的方程：$Q^* = S + R'Q, (RS = 0)$。~~（此处方程与 EE103 数字系统有差异，但与维基百科一致，应该是 EE103 错了）~~

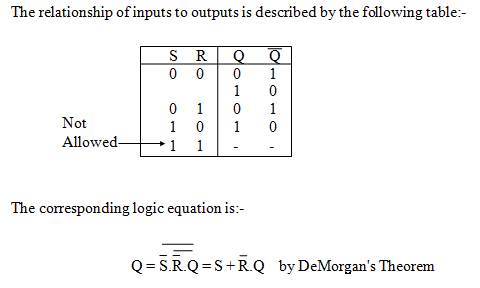
延迟与时钟信号

另外，根据上面的电路图和时间轴，可以得知：

如果要设一，需要保持 $S, R = 1, 0$ 至少两个单位延迟时间 $2 \Delta t$
如果要清零，需要保持 $S, R = 0, 1$ 至少两个单位延迟时间 $2 \Delta t$

也就是说设一和清零的操作，都需要保持相应的输入状态（激活）至少两个单位时间，才能让 $Q$ 获得期望的输出。$Q$ 获得期望输出之后，$R$ 和 $S$ 就可以都灭活了。

然而，虽然 $Q$ 仅需两个单位延迟时间，但是 $Q'$ 需要三个单位延迟时间才能得到。尽管如此，灭活还是仅需等待两个单位时间，因为灭活后不会影响到 $Q'$ 的值。

SR 锁存器可以在输入端加上一个时钟信号 $C$，$C$ 与 $S$，$R$ 分别 NAND 起来之后再传给后面（省略了 NOT 门）。

需要注意，时钟信号 $C$ 的一个取值，必须持续至少 $2 \Delta t$ 的时间；同时，$C = 1$ 的时候，$RS$ 两个输入不应发生改变。这样才能保证电路的正常运行。

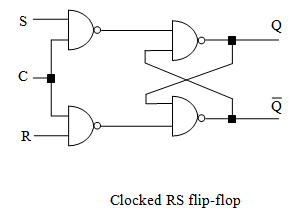
加入时钟信号后，特征方程就可以改为 $Q_{n+1} = S_n + {R_n}'Q_n$ 了。

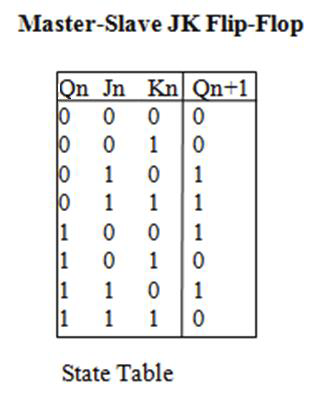
JK 触发器

JK 触发器和触发器中最基本的 RS 触发器结构相似，其区别在于，RS 触发器不允许 $R$ 与 $S$ 同时为 $1$，而 JK 触发器允许 $J$ 与 $K$ 同时为 $1$。当 $J$ 与 $K$ 同时变为 $1$ 的同时，输出的值状态会反转。也就是说，原来是 $0$ 的话，变成 $1$；原来是 $1$ 的话，变成 $0$。

观察 JK 触发器的结构会发现，其实就是在输出端的交叉回授（feedback），也就是把 $Q$ 的值回授给 $K$，$Q'$ 回授给 $J$。当然了，从计算出 $Q$ 和 $Q'$ 再到回授的过程，是有一定延迟的。

为了与 RS 触发器进行区分，以后将 $S$ 改名 $J$，$R$ 改名 $K$。

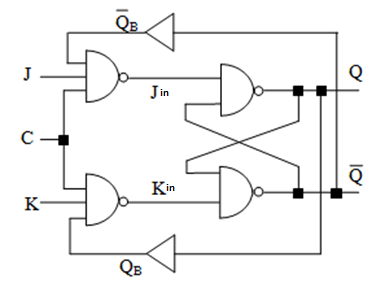
变化示意图：

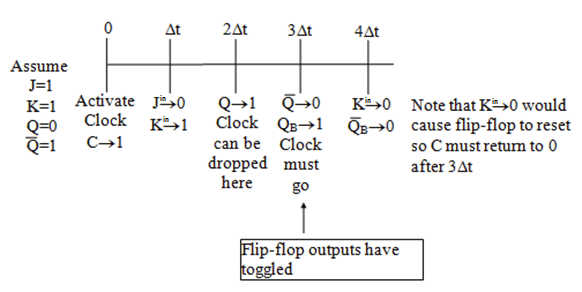
由上图可知，必须保证时钟信号的时间范围在 $[2\Delta t, 3\Delta t]$ 之间，否则输出值会回过头过来影响输入的值。即，$2 \Delta t$ 的时候可以撤走时钟信号，$3 \Delta t$ 的时候时钟信号必须撤走，否则就坏大事儿了！

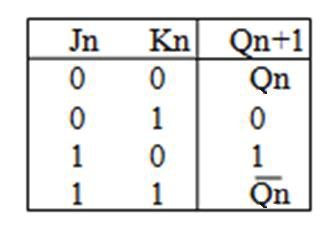
若能保证时钟信号的持续时间在此范围内，则 JK 触发器的状态表如下

那么，就需要设计一种电路，能提供精准时间范围的时钟信号。

（边沿触发）脉冲整形电路 Pulse Shaper Circuit

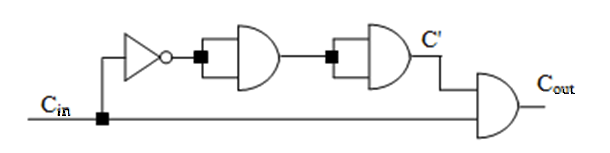
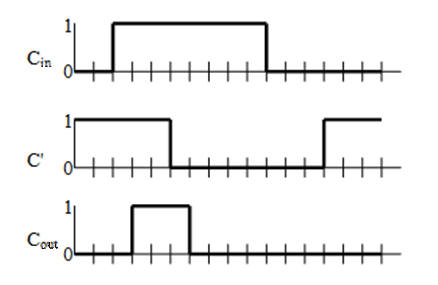
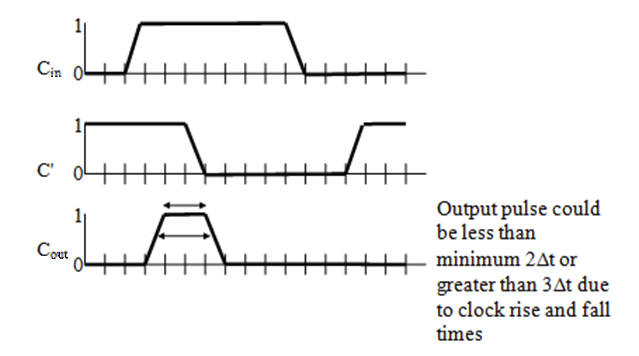
像这样。时钟信号未被激活的时候，即 $C_{in} = 0$ 的时候，上路值是 $1$，下路值是 $0$，这时候最后的 AND 门输出的 $C_{out} = 0$。

一旦 $C_{in}$ 变成了 $1$，下路立即变成 $1$，而上路要等 $3\Delta t$ 的时间，所以这时候 $C_{out}$ 会有 $3 \Delta t$ 的激活时间（前提是 $C_{in}$ 也要保持至少 $3 \Delta t$ 激活状态）。$3\Delta t$ 时间过后，$C_{out}$ 变成 $0$。

也就是说，上路的值的变化，总是比下路要慢 $3 \Delta t$ 的时间。

于是，这就构造出来了一个，最长维持 $3\Delta t$ 的时钟信号。

如果把这种东西当作时钟信号输入给 JK 触发器，那么这就是一个 边沿触发（edge-triggered） 的 JK 触发器，即仅在时钟的有效边沿期间接受 $J$ 和 $K$ 输入。

上面这个图太理想化了。实际上，$0$ 和 $1$ 之间不是瞬间变化的，而是逐渐的。比如，实际情况很可能是这个样子，于是实际的时钟信号时间会很有可能不在 $[2\Delta t, 3 \Delta t]$ 范围内。

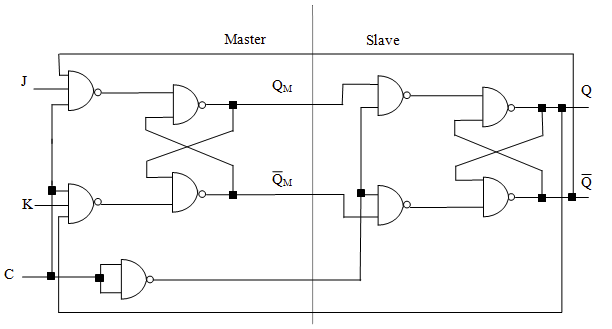
（脉冲触发）主从 JK 触发器（Pulse Triggered Master Slave JK Flip Flop）

上述问题，可以用主从触发器来解决。主从触发器，顾名思义，是由两个触发器构成的，一个是 主触发器（master），另一个是 从触发器（slave）。它们之间用一个反相器（或同输入的 NAND 门）来连接时钟信号：

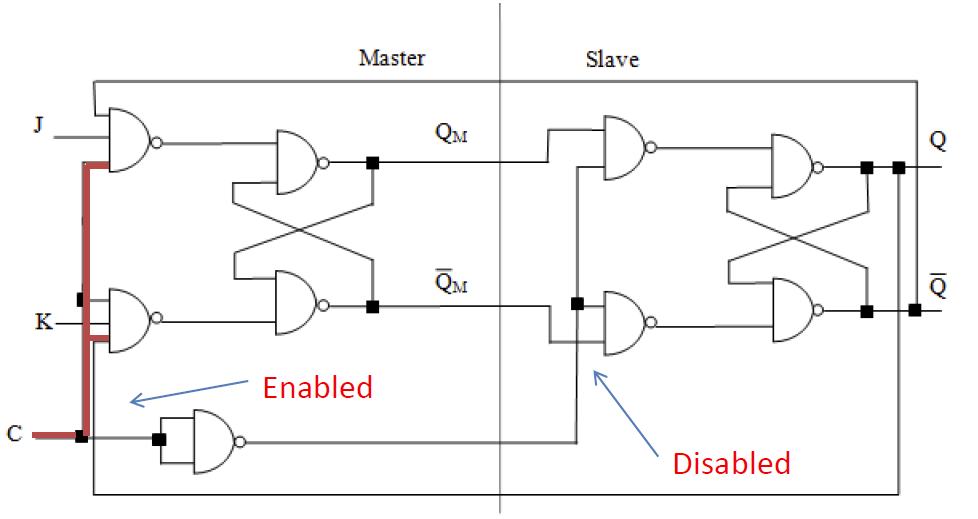
这种结构非常巧妙。最开始，认为时钟信号 $C$ 是 $0$。当时钟信号 $C$ 激活的时候，从触发器接受到的时钟信号就会被置零，于是从触发器就处于未激活的状态。即：此时仅有主触发器会做出响应，从触发器会保持之前的状态不变。（时钟信号需要保持激活状态至少 $3 \Delta t$ 的时间）

当时钟信号从高电平恢复到低电平的时候，主触发器被禁用，从触发器激活，并且从触发器的输出会被置成主触发器输出，也就是保持一致。最后，我们选取从触发器的输出作为最终输出。（时钟信号需要保持未激活状态至少 $3 \Delta t$ 的时间）

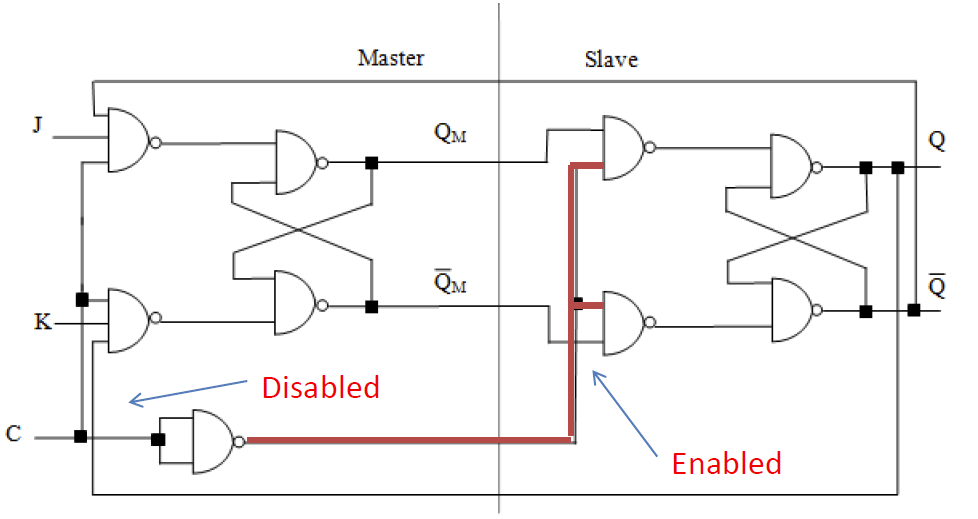
由此可见，在一个时钟周期里，输出端的状态只可能改变一次，而且发生在时钟信号 $C$ 的下降沿，因为只有在这个时候从触发器才会被激活。

知乎上说，边沿触发的输出，取决于边沿时刻的输入信号；而脉冲触发的输出，取决于整个高电平时间内，主触发器的状态。

（电平触发）D 锁存器（D Latch）

D 锁存器是双稳态（bistable）的，类似于 SR 锁存器，只不过是永远维持 $R = S'$（$S = D, R = D'$）；此外，加入了一条激活线（enable line） $G$，类似于时钟信号的作用。

当激活线 $G = 1$ 时，输出 $Q$ 取决于 $D$ 的值。反之，若 $G=0$，则输出 $Q$ 维持不变。

状态表如下：

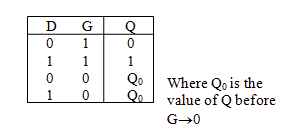
（边沿触发）T 触发器

就是 $J,K$ 永远相等的 JK 触发器。

T 触发器的逻辑功能是：当 $T = 1$ 时，每来一个时钟信号，状态就翻转一次；$T=0$ 则维持不变。

电平触发、边沿触发、脉冲触发的区别

个人理解：

电平触发，就是当时钟信号激活的时候，输出随时跟随输入改变。
边沿触发，就是仅时钟信号上升沿到达的时候，输出才会改变，且仅取决于当前的输入。图示上，在时钟信号的位置用小三角标记表示边沿触发。
脉冲触发，就是仅时钟信号下降沿到达的时候，输出才会改变，但这个输出取决于整个时钟信号激活周期中，主触发器的最终状态，而不是下降沿到达的输入的瞬间状态。图示上，在输出信号的位置用直角符号表示脉冲（也叫延迟）触发。

RS，JK，T，D 触发器的特性方程

SR：$Q^* = S + R'Q$
JK：$Q^* = JQ' + K'Q$
T：$Q^* = T \oplus Q$
D：$Q^* = D$

状态表和激励表（state table，excitation table）

两者差不多就是一正一反的关系。

状态表，用于描述触发器在当前输入组合下的响应。比如前面那些，左边是输入，最右边是输出的，都叫状态表。

激励表则相反。激励表通常左边是输出，右边是输入，也就是：我想要达到目标的输出值，需要什么样的输入值。