Chaper 2 Part 1: Boolean Algebra 布尔代数
(共 42 页)
逻辑门
基本逻辑门,就是 AND,OR,NOT 这仨啦。
观察真值表容易发现,AND 有逻辑乘法的作用,而 OR 有逻辑乘法的作用。NOT,有时候被称作 Inverter。
而 AND 与 NOT 组合,产生了 NAND。OR 与 NOT 组合,产生了 NOR。
EX-OR,全称 exclusive-or,顾名思义,不包含全是 1 的 OR,也就是异或。符号是 $\oplus$。$A \oplus B = A'B + AB'$。
与异或对应的是 EX-NOR,同或,说白了就是异或再接上一个 NOT。
下面表格摘自 EE103 笔记:
常见逻辑门
| gate name | 中文名 | IEEE 符号 | 布尔表达式 | 计算方法 | 备注 |
|---|---|---|---|---|---|
| NOT | 非 | 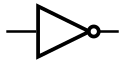 |
$f = \overline{A}$ | 输出反码 | 也叫反相器 Inverter |
| AND | 与 |  |
$f = AB$ | 当且仅当 所有 输入都是 HIGH 才输出 HIGH 否则为 LOW | 执行逻辑乘法 |
| OR | 或 | 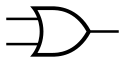 |
$f = A+B$ | 当且仅当 所有 输入都是 LOW 才输出 LOW 否则为 HIGH | 执行逻辑加法 |
| NAND | 与非 |  |
$f = \overline{AB}$ | 当且仅当 所有 输入都是 HIGH 才输出 LOW 否则为 HIGH | |
| NOR | 或非 | 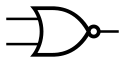 |
$f = \overline{A+B}$ | 当且仅当 所有 输入都是 LOW 才输出 HIGH 否则为 LOW | |
| XOR | 异或 | 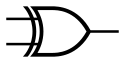 |
$f = A \oplus B$ | 当且仅当 HIGH 的个数是奇数,输出是 HIGH 否则为 LOW | 可以看作二元加法器 |
| XNOR | 同或 | 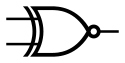 |
$f = \overline{A \oplus B}$ | 当且仅当 HIGH 的个数是奇数,输出是 LOW 否则为 HIGH |
布尔函数
跟数学上的函数基本上一样。比如 $f(A, B, C) = AB' + BC + C'$ 就是一个布尔函数。
对偶函数(dual)
函数的对偶函数(dual),就是把所有的 AND 换成 OR,OR 换成 AND;1 换成 0,0 换成 1;保持原先的变量及其运算顺序(加上适当的括号)。比如上面 $f$ 的对偶函数就是 $f_d(A, B, C) = (A + B')(B + C)C'$。
所有布尔表达式都具有一个与之对应的对偶式 dual。
补函数(complement)
布尔代数领域的补函数就是说,对于 $2^n$ 种变量输入组合,函数值永远与原函数相反。
把对偶函数的每个变量 invert 一下,就可以构造出一个补函数。然而课件里面没说是怎么证明的,就记住这个结论好了。
比如,上面函数 $f$ 的补函数就是 $\overline{f} = (A' + B)(B' + C')C$。
反函数(inverse)
把函数 $f$ 的真值表列出来,$f$ 本身相当于把所有 $f=1$ 的项求 SOP。
而 $\overline {f}$ 相当于把所有 $f=0$ 的项求 SOP。
这里的反函数 inverse 和补函数 complement 是 同一个概念,只是求出来的途径、表达形式不一样。
自足算子 Functionally Completeness
一个运算的集合被称作 functionally complete(或者 universal),当且仅当这几个运算可以表达任何的布尔函数。
例如,{AND, NOT} 就是一个自组算子,因为 NOT 和 AND 可以组合成 NAND,而 NAND 可以表示任意门。同理,{OR, NOT} 也是自足算子(complete set)。
再进一步,NAND 本身构成的集合 {NAND} 就是一个自足算子。
用 NAND(与非)表示其他逻辑运算(CS171)
表示 NOT
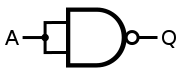
NOT(A) = A NAND A
表示 AND
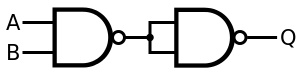
A AND B = ( A NAND B ) NAND ( A NAND B )
表示 OR
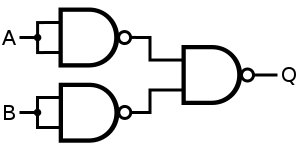
A OR B = ( A NAND A ) NAND ( B NAND B )
表示 NOR
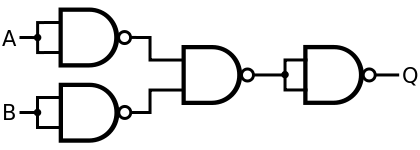
A NOR B = [ ( A NAND A ) NAND ( B NAND B ) ] NAND [ ( A NAND A ) NAND ( B NAND B ) ]
表示 XOR

A XOR B = [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ]
POS 形式的布尔函数
有两种方法,一种是利用对偶函数和反函数,另一种是利用最大项
利用对偶函数和反函数
- 列出真值表
- 给所有 $f=0$ 的求 SOP,即求出反函数(可以用卡诺图)
- 给反函数求对偶函数
- 再把对偶函数的每个变量 invert 一下,就得到原函数的 POS 形式
即:原函数经过对偶再翻转变量,得到反函数;反函数经过对偶再翻转变量,同样可以得到原函数。
利用最大项
所谓 最大项 maxterm,就是一堆变量直接加起来。相对应的 最小项 minterm,就是一堆变量直接乘起来。变量和运算次数相同的时候,最大项写起来长,最小项写起来短。
- 列出真值表
- 找出所有 $f = 0$ 的项,把构成这个项的所有变量 OR 起来。注意,变量值取 0 的不变,取 1 的翻转。
- 把刚才求出来的所有 S 给乘起来,就得到了 POS
如,$f = \Sigma(1,2,3,5) = \Pi(0,4,6,7)$ 这个函数:
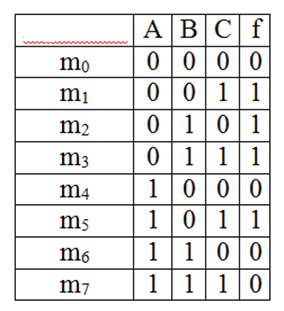
- 第一个 $f=0$ 的行,变量取值是 $0,0,0$,因此对应 $A+B+C$
- 第二个 $f=0$ 的行,变量取值是 $1,0,0$,因此对应 $A' + B + C$
- 以此类推,最终得到:$f(A,B,C) = (A + B + C)(A' + B+ C)(A' + B' + C)(A' + B' + C')$
布尔运算的基本性质与运算律
AND
$A.0 = 0$
$A.1 = A$
$A.A' = 0$
$A.A = A$
OR
$A+0 = A$
$A + 1 = 1$
$A + A' = 1$
$A + A = A$
NOT
$A = A''$
运算优先级(Operator Precedence)
概括来说,就是 NOT > AND > OR。
因为 NOT 的运算与符号后面的 atom 直接融为一体,而 AND 的运算优先级总是高于 OR 的。
布尔运算的运算律
交换律 Commutation
- $A + B = B + A$
- $AB = BA$
结合律 Association
- $A + (B + C) = (A + B) + C$
- $A(BC) = (AB)C$
分配律 Distribution
- $A + BC = (A + B)(A + C)$
- $A(B + C) = AB + AC$
吸收律 Absorption
- $A + AB = A$
- $A(A + B) = A$
理解:
- $A + AB = A \cdot 1 + AB = A(1 + B) = A$
- $A(A + B) = AA + AB = A + AB = A$
一致律 Consensus
- $AC + BC' = AB + AC + BC'$
- $(A + C)(B + C') = (A + B)(A + C)(B + C')$
推导:
- $\begin{aligned} \text{等式右侧} &= AB + AC + BC' \\ &= AB(C + C') + AC(B + B') + BC'(A + A') \\ &= ABC + ABC' + ABC + AB'C + ABC' + A'BC' \\ &= ABC + ABC' + AB'C + A'BC' \\ &= AB(C + C') + B'C(A + A') \\ &= AB + B'C \\ &= \text{等式左侧} \end{aligned}$
- $\begin{aligned} \text{等式右侧} &= (A+B)(A+C)(B+C') \\ &= (A + BC)(B + C') \\ &= AB + AC' + BC \\ &= AB + AC' + BBC + BCC' \\ &= AB + AC + BC + CC' \\ &= A(B + C') + C(C + C') \\ &= (A + C)(C + C') \\ &= \text{等式左侧}\end{aligned}$
德摩根律
$(A + B)' = A'B'$
$(AB)' = A' + B'$
CS172 笔记摘录
| 运算律 | 示例 1 | 示例 2 |
|---|---|---|
| 交换律 | $p \wedge q = q \wedge p$ | $p \vee q = q \vee p$ |
| 结合律 | $(p \wedge q) \wedge r = p \wedge (q \wedge r)$ | $(p \vee q) \vee r = p \vee(q \vee r)$ |
| 分配律 | $p \wedge(q \vee r) = (p \wedge q) \vee(p \wedge r)$ | $p \vee(q \wedge r) = (p \vee q) \wedge(p \vee r)$ |
| 德摩根 | $\neg(p \wedge q) = (\neg p) \vee(\neg q)$ | $\neg(p \vee q) = (\neg p) \wedge(\neg q)$ |
| 吸收律 | $p \vee(p \wedge q) = p$ | $p \wedge(p \vee q) = p$ |
| 条件句 | $(p \rightarrow q) = (\neg p \vee q)$ | $\neg(p \rightarrow q) = (p \wedge \neg q)$ |
布尔表达式化简示例
$$\begin{aligned} F &= (A + B)(A + B')(A' + C) \\ &= (AA + BB')(A' + C) \\ &= (A + 0)(A' + C) \\ &= AA' + AC \\ &= 0 + AC \\ &= AC \end{aligned}$$