跳转至

Lecture 17. Relational Algebra and Query Planning in SQL and More Referential Integrity 关系代数、查询过程、参照完整性

首先声明：关系代数虽然写成数学里的代数形式，但其实跟数学里面的代数没啥关系，不过它是基于集合论的。

关系代数是用于给关系数据库当中的数据进行建模，同时定义查询的。

关系代数的主要应用是，给关系数据库提供理论基础。

关系代数的五种运算分别是：

  • selection
  • projection
  • 笛卡尔积 Cartesian product（也叫 cross join）
  • 集合并 set union
  • 集合差 set difference

在 DBMS 当中对于关系的底层操作，都类似于关系代数的操作。

把关系视作 tuple 的集合（不允许重复）。

SQL 是 declarative 的。也就是说只需要告诉 DBMS 想干什么，而不用告诉他如何一步步的实现。

简单关系代数示例

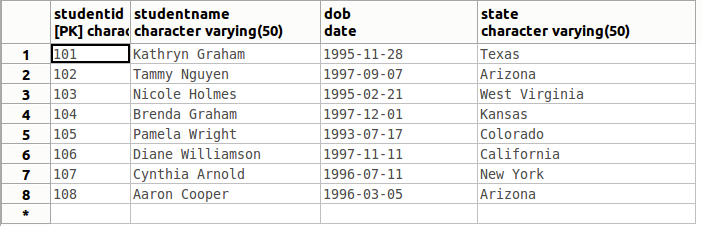
image-20221118103557378

以这张 Student 表为例。在关于代数中，用 $S$ 表示这张表。

projection

用数学符号 $\pi$ 表示。相当于 SQL 当中的 SELECT。$\pi(A)(B)$ 相当于在集合 $B$ 当中取出子集 $A$。

如，SELECT studentname, dob FROM student 可以表示为 $\pi(\texttt{studentname, dob})(S)$。

selection

用数学符号 $\sigma$ 表示。相当于 SQL 当中的 WHERE。为了跟 SELECT 进行区分，有时候叫做 restriction。

如，WHERE dob > '2000-12-31' 可以表示为 $\sigma(\texttt{dob > '2000-12-31'})(S)$

projection 和 selection 的结合

就相当于带有 WHERE 条件的 SELECT。

比如，SELECT studentname, dob FROM student WHERE dob > '2000-12-31' 可以写成：$\pi(\texttt{studentname, dob})(\sigma(\texttt{dob > '2000-12-31'}))(S)$。

带有 AND 的 WHERE

比如如果 WHERE 当中的条件是：SELECT xx FROM yy WHERE A > B AND C > D，写成关系代数，就是 $\pi(xx)(\sigma(A>B)\&\&(C>D))(yy)$。

规律总结

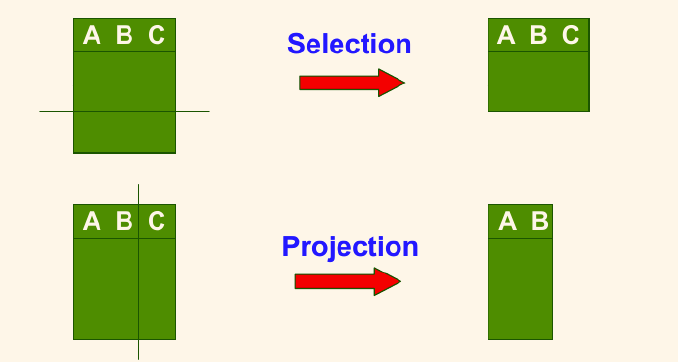
可以发现，$\pi$ 和 $\sigma$ 都是相当于一元的操作。$\sigma$ 是横向切割，$\pi$ 是纵向切割。

image-20221118105018028

关系代数中的笛卡尔积

笛卡尔积直接用乘号 $\times$ 表示。

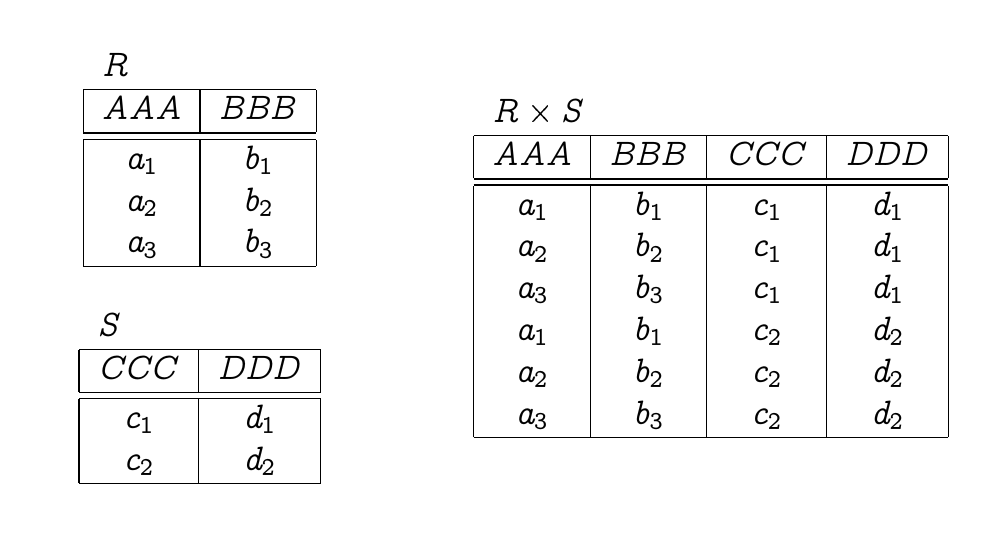
image-20221118105205907

可以看到，$R$ 有三行，$S$ 有两行，每行想象成一个 tuple，所以相乘得到六行（$3 \times 2$个 tuple）。$R$ 两列，$S$ 两列，乘起来就是（$2+2=4$）。注意行的变化是乘法，列的变化是加法，不要搞混了。

在 SQL 当中，SELECT * FROM T1, T2 就相当于把 T1 和 T2 两张表做了个笛卡尔积。

关系代数当中的 join

用数学符号 $\bowtie$ 表示。join 用于连接具有相同属性的两个关系（表）。

条件 join

表示为 $E_1 \bowtie_{\text{condition}} E_2$，相当于 $\sigma_{\text{condition}}(E_1 \times E_2)$。

自然 join

表示为 $E_1 \bowtie E_2$。DBMS 计算自然 join 结果的过程如下：

  1. 先直接计算 $E_1 \times E_2$ 的笛卡尔积。如果有重复的属性（列），就先重命名一下。
  2. 然后删掉所有重复的地方不相等的行。
  3. 把重复属性合并。

说白了，共享列就是用来删行的。如果没有共享列，那就相当于直接笛卡尔积了。

自然 join 的例子

例一

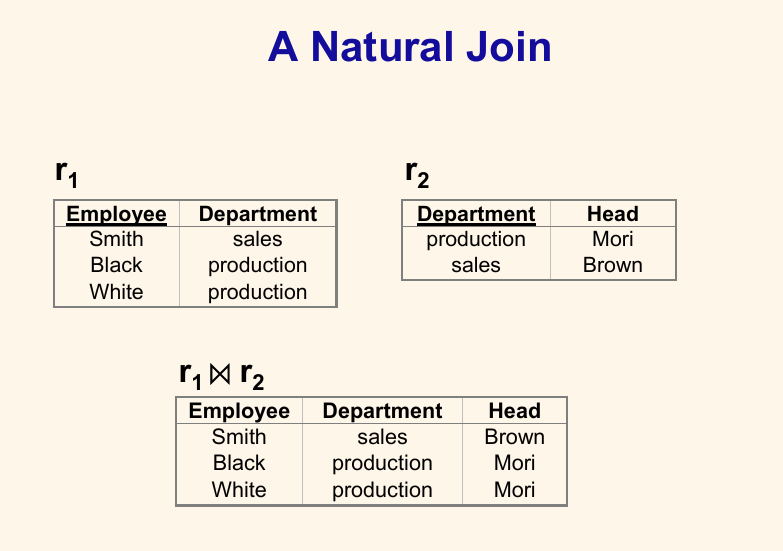
image-20221118111642599

如果 $r_1$ 和 $r_2$ 先直接笛卡尔积，会产生六（$3 \times 2$）行、四（$2+2$）列。列分别是：$E, D_1, D_2, H$。

然后顺着每一行去检查。如果有某一行 $D_1 \not= D_2$，就把这一行删掉。在这个例子当中，总共有三个被删了。

最后再把 $D_1$ 和 $D_2$ 合并成一个 $D$（反正俩是相等的）。

例二

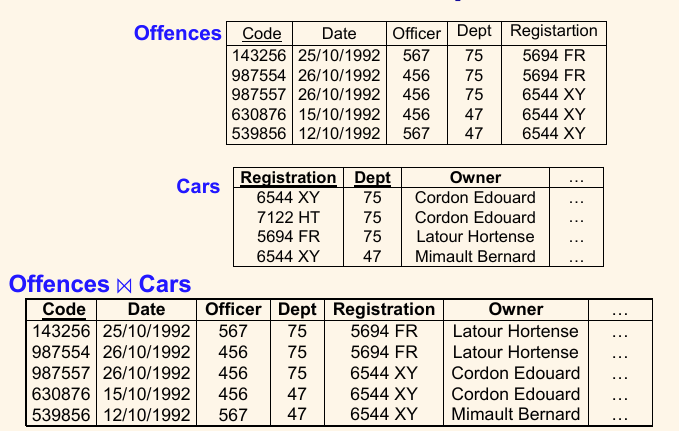
image-20221118112149826

这个例子当中，两个要 join 的表，不仅有一个列相同（共享）。这种情况下，每一对共享列删掉一个留一个。

但是考试的时候，全都列出来再删，太麻烦了！一种简单方法是：对于第一个表当中的每个行，用共享列直接去找第二个表当中与之匹配的，单独做笛卡尔积，然后合起来。

例三

image-20221118112815715

既然共享列是用来删行的，那么就有把行删光的可能性。

通常的 join 都是跟外键 foreign key 有关的，然而这里 $r_2$ 的 D 不是外键（外键必须出现在另一个表里），造成了这种删光的现象。

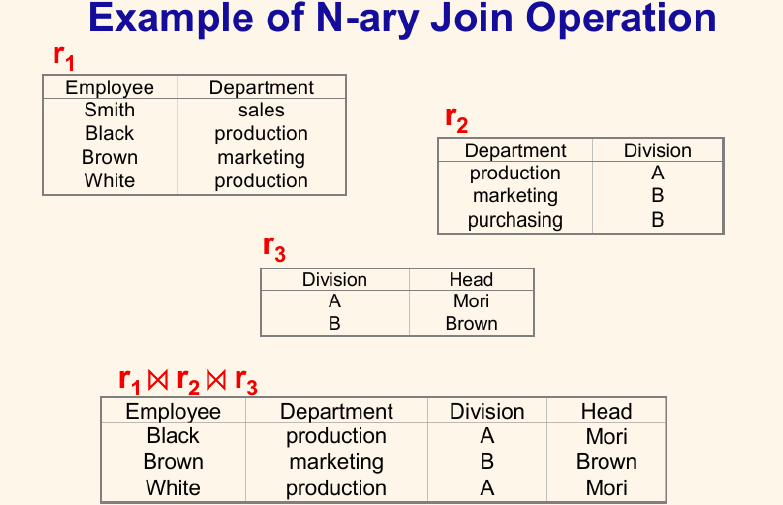
例四：多次 join

image-20221118113257568

SQL 的 join 翻译成关系代数式子

其实，关系代数式子只能有一种，但是不同的 SQL 当中可能会有不同的表达。所以说只有关系代数是准确的。

例一

~~（晕）~~

SELECT co.name, cp.name
    FROM cp, ap, co
    WHERE (co.r = ap.r) AND (cp.id = ap.id) AND (co,name like '%L%');

翻译之后：$\pi(\texttt{co.name, cp.name}) (\sigma(\texttt{co.name like '\%L\%'})( (\texttt{co}\bowtie_{\texttt{r = r}}\texttt{ap}) (\texttt{cp} \bowtie_{\texttt{id = id}} \texttt{ap})))$。

例二

~~？？？~~

画成树状图会比较好看一点

叶子节点代表的是表，也就是关系的集合。

询问过程 Query planning

询问过程是一个有序集合，表示如何一步一步的访问数据，也就是表示了一个过程。

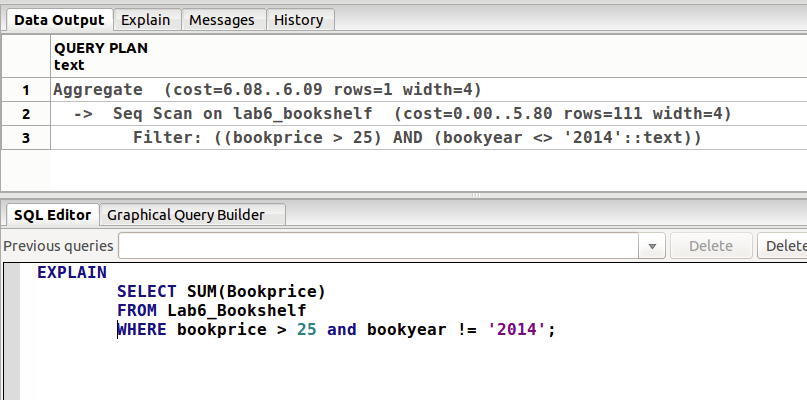
EXPLAIN 关键字

Postgre SQL 当中，用 EXPLAIN 关键字可以打印出 SQL 语句的执行过程。如：

EXPLAIN <...>

image-20221125102402709

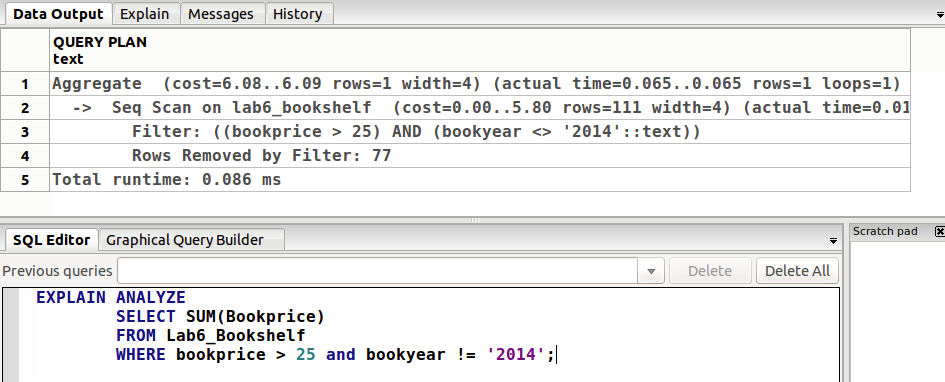
EXPLAIN ANALYZE 关键字

一个例子

EXLLAIN ANALYZE <...>

image-20221125102918147

另一个例子（Having）

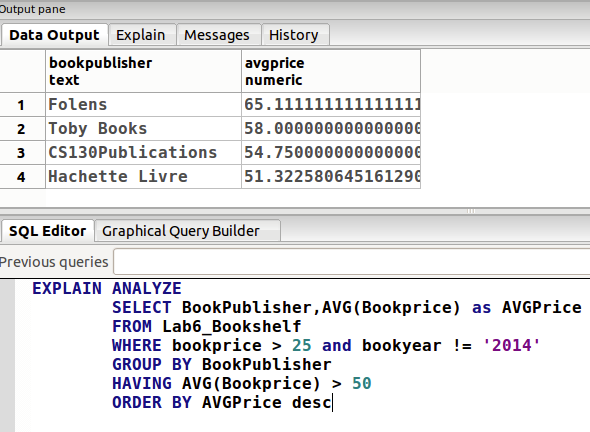
image-20221125103517248

这个例子里面的输出是 hash aggregate，刚才是 aggregate。因为 GROUP BY 分组类似哈希表。~~

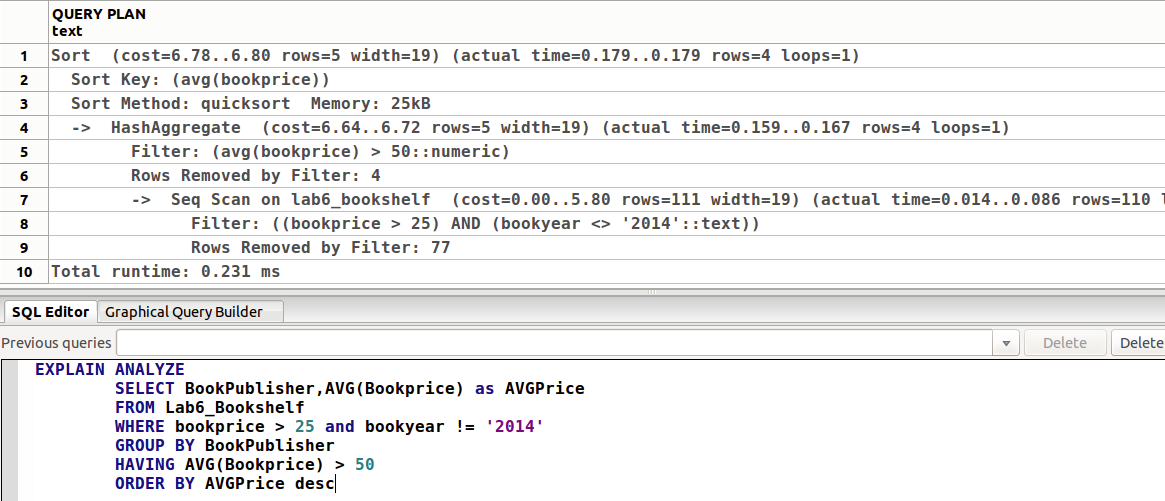
image-20221125103201712

再一个例子（join）

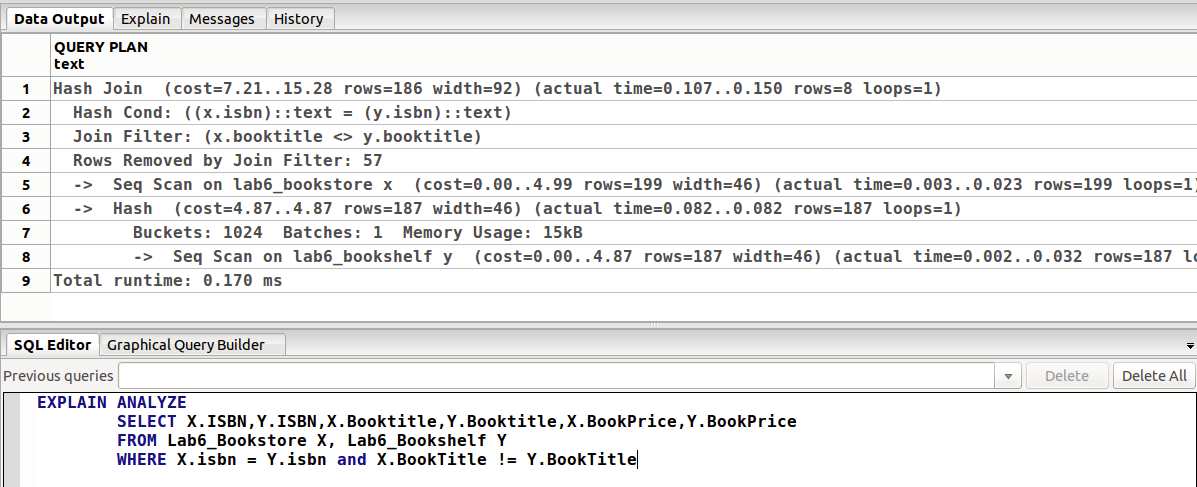
image-20221125103640021

函数

用 PREPARE 关键字，搞一个类似于函数的东西（好像这里叫做模板 template），然后再传参调用，可以简化重复的代码部分。其中，$1 和 $2 分别代表第一个和第二个参数（parameter）。

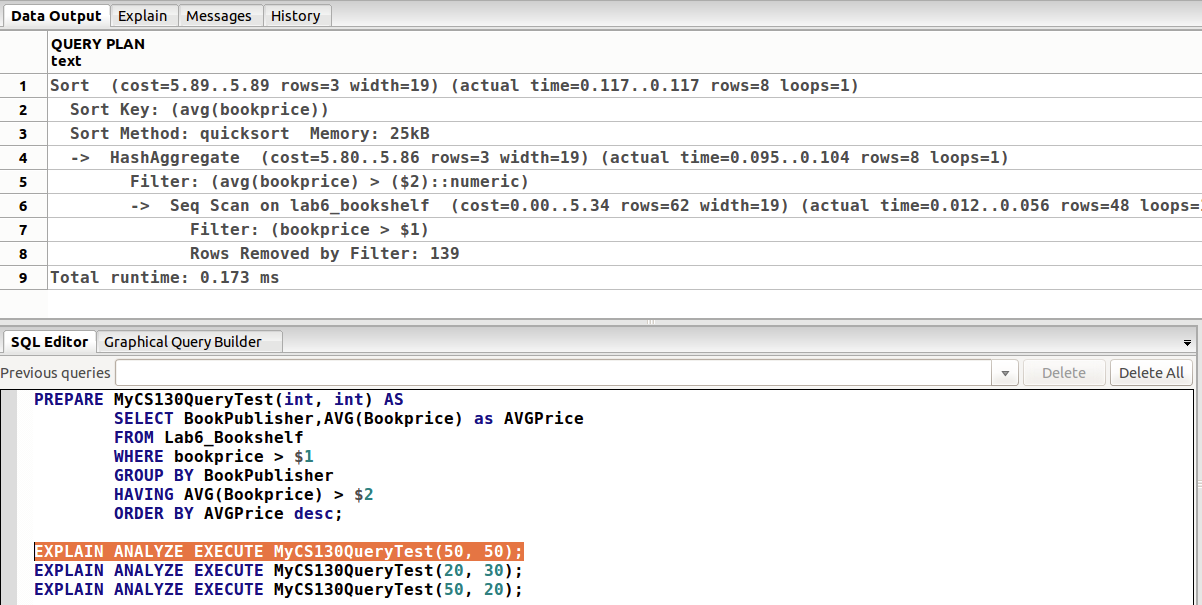
image-20221125104125460

Query Planner

~~就一页 ppt ，不知道讲了啥。。。~~