Chapter 8 比较两个对象
- treatment:处理组
- experimental unit:实验单元
-
response:响应
-
例子 8.1,专家组,新手组,独立样本设计(independent sample design),在课本 266 页
- 还有例子二,土木工程师,研究车道油漆耐用性的
考虑:
- 独立样本
- 配对的样本
关于独立的大样本的假设
若:
- 样本 $X_1, X_2, \cdots, X_n$ 来自均值、方差分别为 $\mu_1, \sigma_1^2$ 的一号总体
- 样本 $Y_1, Y_2, \cdots, Y_n$ 来自均值、方差分别为 $\mu_2, \sigma_2^2$ 的二号总体
- 两个样本都是大样本($n_1\geq 30$,$n_2\geq 30$)且相互独立
则两个样本的均值的差值,服从正态分布。形式化的说就是: $$\boxed{Z = \frac{\overline X - \overline Y - \delta}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}}$$,$Z \sim N(0, 1)$,因为 $\overline X - \overline Y \sim N(\mu_1-\mu_2, \frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2})$,其中用 $\delta$ 表示两个样本均值的差值($\delta = \mu_1-\mu_2$)。反正对于大样本,已知 $\sigma$ 就用 $\sigma$,不然就用 $S$ 代替。
跟第七章类似。样本均值的差的 $(1-\alpha)100\%$ 置信区间是:$$\boxed{(\bar x - \bar y) \pm z_{\alpha/2}\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}}$$。
对于原假设 $H_0: \mu_1-\mu_2 = \delta_0$,$Z$ 是刚才上面那一坨,表格如下(其实跟第七章的基本一样)
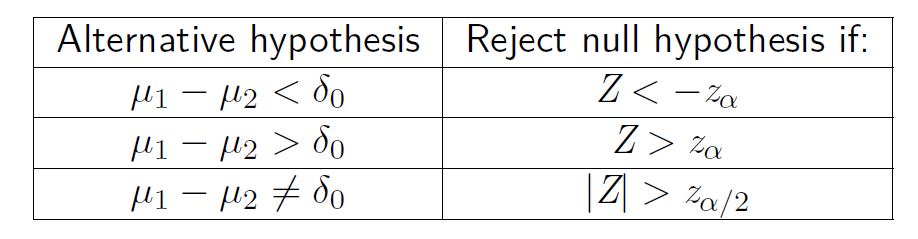
关于独立的小样本(等方差)的假设
注意,对于小样本的题目,必须满足总体服从正态分布才可做!但是对于大样本,就没有这个限制。因为 大样本小样本的区别就在于中心极限定理。大样本无论什么总体分布可以用正态分布,小样本只有总体服从正态分布的时候才能用正态分布,否则用 t 分布。
对于大样本来说,如果方差未知,直接用样本标准差代替就好了;但是对于小样本来说,不能直接用标准差代替。
对于两组小样本方差相差不大的情况,可以池化(pool),就是两组扭起来,以此来估算总体方差 $\sigma^2$:$$S_p^2=\frac{\sum_{i=1}^{n_1}\left(X_i-\bar{X}\right)^2+\sum_{i=1}^{n_2}\left(Y_i-\bar{Y}\right)^2}{n_1+n_2-2}= \boxed{\frac{\left(n_1-1\right) S_1^2+\left(n_2-1\right) S_2^2}{n_1+n_2-2}}$$,这个东西 $$t=\frac{\bar{X}-\bar{Y}-\delta}{S_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$$ 服从 t 分布,自由度是 $\boxed{n_1+n_2-2}$.
$(1-\alpha)100\%$ 的置信区间是 $$(\bar{x}-\bar{y}) \pm t_{\alpha / 2} \cdot S_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}$$,还是移项算出来的,其中 t 的自由度是 $n_1+n_2-2$.
小样本,不等方差
t 发生了变化$$t^{\prime}=\frac{\bar{X}-\bar{Y}-\delta}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}$$,自由度也不再是整数,而是 $$\frac{\left(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}\right)^2}{\frac{\left(S_1^2 / n_1\right)^2}{n_1-1}+\frac{\left(S_2^2 / n_2\right)^2}{n_2-1}}$$。这个方法是比较近似的,不是精确解,名叫 Smith-Satterthwaite test.
$(1-\alpha)100\%$ 的置信区间是 $$(\bar{x}-\bar{y}) \pm t_{\alpha / 2} \cdot \sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}$$。
算这个实在太麻烦了,所以说,在实际应用当中,如果方差相差不大(三倍以内),一般就当作等方差了。
配对比较
刚才是不配对的,现在研究一下配对的(很简单)。配对意思就是 $X_i$ 与 $Y_i$ 一一对应了。定义 $D_i = X_i - Y_i$,所以本质上就变成一个变量的问题了。