Chapter 2 描述数据的方法

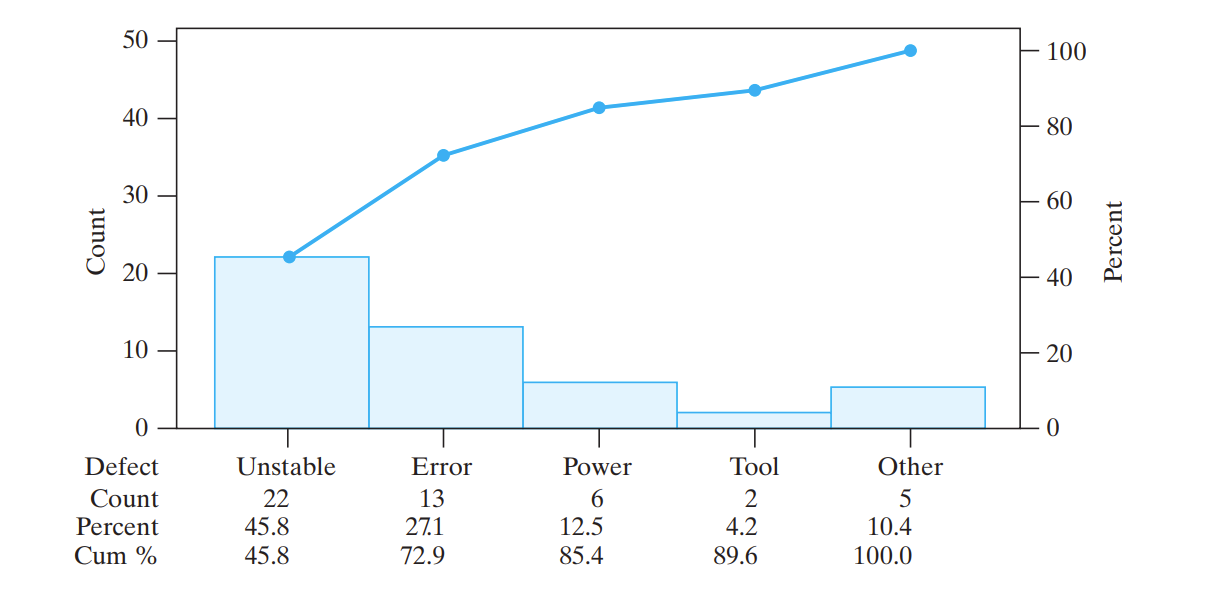
帕累托图 Pareto Diagrams

条形图和折线图的结合。

差不多就是，几个数据，最多的放左边，最少的放右边，Other（其他）放在最右边，条形柱子表示数量，百分比的前缀和用折线图。

这样，最左边的通常就是比较主要的数据。

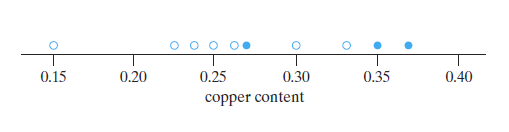
散点图 Dot Diagrams

两点作用。

可以很方便的看出异常值（离群值）。离群值 outlier，比如一堆几十的混进去一个几万的，无论是不是测量错误，都需要特殊关照。
感官上区分两组数据是否不同。比如实心点表示第一次测量，虚线点表示第二次。如果第一次普遍在左边，第二次普遍在右边，那么两组就明显数据不同。

频率分布 Frequency Distributions

几十个数据，一般分成五六个区间（等距、等间隔）。然后统计每个区间内的数量，换算成频率。应当是左闭右开或者左开右闭。

max 和 min 不一定是左端点或者右端点。比如 max 可能是 388，右端点可以取 400，好算。

最大的缺点是，位于一个区间内的数据出现了多少次，能知道，但是这个数字具体是谁，不知道。有一种不太精确的解决方案，是用一个区间的中点的值，作为 class mark，代表这个区间的所有数。

也有一种，把频率换成了前缀和。

频率分布（直方）图

通常，频率分布图都是 histogram（柱状图），常见的是频率分布直方图。

横坐标可以标注区间，也可以标注 class mark。

有单峰（peak）、双峰、斜的……

有的图纵坐标是个数，也有的图纵坐标是 $\frac{\text{相对频率}}{区间宽度}$。这样，所有条柱的面积总和就是 $1$。这种叫做 密度柱状图 density histogram。这种处理方式是「归一化」。

茎叶图 Stem-and-Leaf Displays

频率图可以知道有 $x$ 个数在某个区间里，但是不知道具体是多少。茎叶图可以直观地看出来一个区间有多少个数字，还能保留原始数据。

然而一般茎叶图都是，每 10 个分一个区间。左侧（stem，茎）记录抠掉个位的，右边（leaf，叶）是个位。

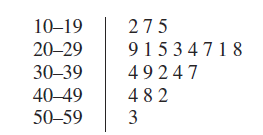
描述测量 Descriptive measures

平均值 sample mean，$$\bar x = \frac{1}{n} \times \sum_{i=1}^n x_i$$
中位数 sample median，若 $n$ 是奇数，就是第 $\frac{n+1}{2}$ 个；若 $n$ 是偶数，就是第 $\frac{n}{2}$ 和 $\frac{n}{2}+1$ 个的平均。

中位数不容易被少数的异常值影响。如：$[10, 10, 10, 10, 200]$。

在统计学中，异常值是指与其他观测值有显著差异的数据点。异常值可能是由实验误差造成；后者有时会从数据集中排除。异常值可能会导致统计分析中出现严重问题。能妥善处理异常值的估计量，称为“稳健”。例如，中位数是集中趋势的稳健统计量，但平均数则不然。

样本方差 sample variance，描述偏离程度，$$s^2 = \frac{\sum_{i=1}^{n}(x_i - \bar x)^2 }{n-1} = \frac{ \sum_{i=1}^{n}x_i^2 - \frac{(\sum_{i=1}^{n}x_i)^2}{n}}{n-1}$$，这个等式可以用完全平方公式推导。关于分母为啥是 $n-1$ 不是 $n$，大概原因是因为这个式子的分子永远偏小，所以调整一下分母，具体原因后面再推。可参考知乎.
标准差 standard deviation，$s = \sqrt{s^2}$
相对方差 relative variation，$V = \frac{s}{\bar x} \times 100\%$，意义参考课本 P39 E13

推导方差

对于独立的随机变量 $X_1$, $X_2$，有 $$\begin{aligned}0 &= E[(X_1-\mu_1)(X_2-\mu_2)] \\ &= E(X_1X_2-\mu_1X_2-\mu_2X_1+\mu_1\mu_2) \\ &= E(X_1X_2)-\mu_1E(X_2) - \mu_2E(X_1)+\mu_1\mu_2 \\ &= E(X_1X_2)-\mu_1\mu_2-\mu_2\mu_1+\mu_1\mu_2 \\ &= E(X_1X_2)-\mu_1\mu_2\end{aligned}$$，因此 $$E(X_1X_2)=\mu_1\mu_2$$ 于是： $$\begin{aligned}& E\left(\sum_{i=1}^n\frac{\left(X_i-\overline{X}\right)^2}{n-1}\right) \\ =& \frac{1}{n-1}\sum_{i=1}^nE\left(X_i-\overline{X}\right)^2 \\ =& \frac{1}{n-1}\sum_{i=1}^nE\left(X_i^2-2X_i\overline{X}+\overline{X}^2\right) \\ =& \frac{1}{n-1}\sum_{i=1}^nE\left(X_i^2-2X_i\frac{\sum_{j=1}^nX_j}{n}+\left(\frac{\sum_{j=1}^nX_j}{n}\right)^2\right) \\ =& \frac{1}{n-1}\sum_{i=1}^n\left(\sigma^2+\mu^2-\frac{2}{n}\left((n-1)\mu^2+\sigma^2+\mu^2\right)+\frac{\sigma^2}{n}+\mu^2\right) \\ =& \frac{1}{n-1}\sum_{i=1}^n\left(\sigma^2+\mu^2-2\mu^2-\frac{2}{n}\sigma^2+\frac{\sigma^2}{n}+\mu^2\right) \\ =& \frac{1}{n-1}n\frac{n-1}{n}\sigma^2 \\ =& \sigma^2\end{aligned}$$

四分位、百分位 Quartiles and Percentiles

（这个概念的定义不同教材可能不同）

直观理解，中位数就是排在 50% 位置的，那么第一二三四分位就分别是 25%，50% 和 75% 位置的，分别表示为 $Q_1, Q_2, Q_3$。百分位，就是任意百分之几位置的。

具体定义，$100p$-th 的数，就代表至少有 $100p\%$ 的数小于等于它，也有至少 $100(1-p)\%$ 的大于等于它。计算方法就是，先排序，若 $np$ 不是整数，然后计算出 $k = \lceil np \rceil$ 的值，那么第 $k$ 个就是；如果 $np$ 是整数，那么第 $np$ 和第 $np+1$ 个的平均值就是。

极差 range 就是最大值减去最小值。四分位距 interquartile range 就是 $Q_3 - Q_1$。

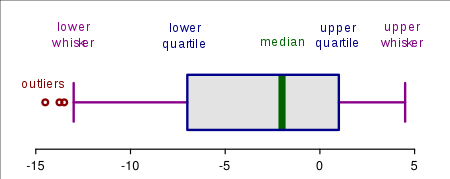
箱线图 boxplot

表示从 $Q_1$ 到 $Q_3$ 的数据；是个方块；方块以外用横线表示。

中间那条竖线是 $Q_2$，也就是中位数。

但是不能体现异常值。

修正箱线图 modified boxplot

可以体现异常值。原理就是，如果最大值与 $Q_3$ 的距离在 1.5 倍箱线长度之内，就正常画线；否则，线画到 1.5 倍以内最远的一个数据，将离群值用圆点标注。$Q_1$ 那一段同理。

注意，修正箱线图的边界，是 正常值范围内的最大/最小值，而不是正常值范围。