Lecture 5. 进程调度 3 关于进程调度的数学建模（26 页）

多进程的性能

队列定理

多处理器系统的队列组织

分布式系统

实时系统

使用两个处理器，并不一定能带来两倍的性能提升，因为调度会变得更复杂，而对于 IO、内存、系统代码的 争吵（contention），以及为了维护 缓存一致性（cache coherency），都会导致一定的性能损失。

排队论 Queuing Theory

概括来说，就是为了最大化吞吐量，减少排队时间。

在建模之前，必须先搞清楚如下三点：

任务到达的模式，比如按照约定时间到达、一群人结伴到达、固定时间到达、随机到达
如何安排排队和调度，队列可能也不止一个，有 VIP 的，有普通的，有的人可能嫌排队太久还会中途离开
服务可提供的容量

排队论就是通过建模，帮助管理者分析怎样才能达到最佳。

关于进程的数学建模（泊松分布、指数分布）

可以认为计算机当中进程的到达模式是随机到达，且同一时间只会到达一个进程，且每个进程之间是相互独立的。

设 $\lambda$ 表示平均单位时间内进程到达的数量，于是就可以研究泊松分布研究，一段时间内到达指定数量的进程的概率是多少。

泊松分布指出，单位时间内到达 $k$ 个事件的概率为：$$P = \frac{\lambda^k e^{-\lambda}}{k !}$$。ST211 当中有学到过说，若 $\lambda$ 是整数，那么 $f_{\max}(x;\lambda) = f(\lambda-1;\lambda) = f(\lambda;\lambda)$；若 $\lambda$ 不是整数，则 $f_{\max}(x;\lambda) = f(\lfloor\lambda\rfloor;\lambda)$，如图：

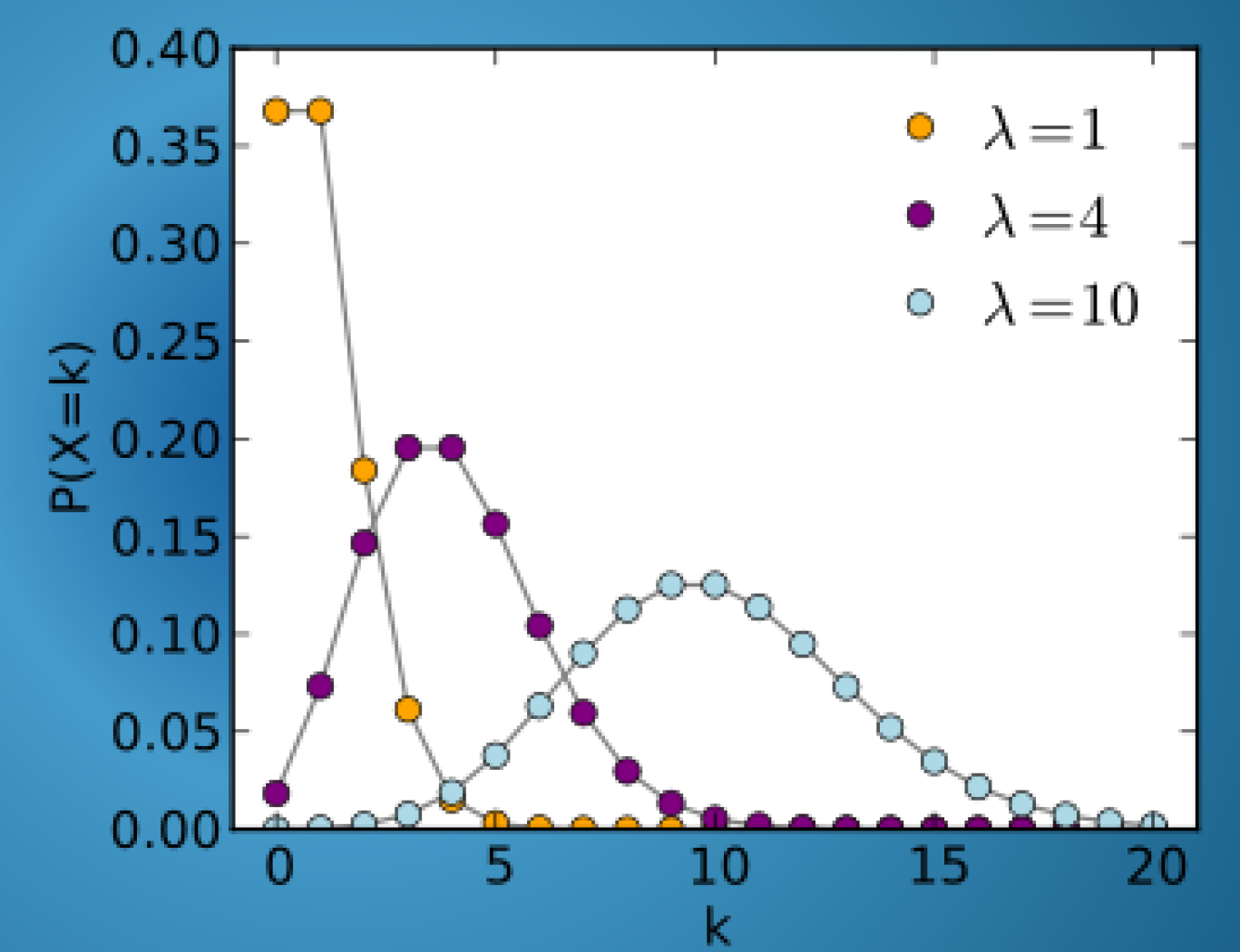
然后假设计算机当中所有的进程只要进入队列，再执行完成之前都不会离开。

设 $\mu$ 表示单位时间内平均可以处理的进程的数量。（这里就是指数分布了）。

于是平均每个进程的周转时间，根据一些奇怪的数学知识，可以算出来，就是 $\frac{1}{\mu-\lambda}$。

对于多核系统，如果每个核的队列都有一个队列，那么每个核都是 $T = \frac{1}{\mu-\lambda}$。如果所有核心公用一个队列，那么 $T_1 = \frac{1}{n\mu-n\lambda} = \frac{T}{n}$，可以变得更快，前提是每个处理器都不停的繁忙工作。

其它系统

分布式系统

分布式系统就是通过网络把一堆电脑连接起来。分布式系统的调度应当尽量让每一台电脑的负载差不多平衡。

分布式系统由于涉及到了网络，有网络延迟、丢包等等因素影响，所以调度起来非常复杂。

实时系统 real time

工厂生产线，原材料在一端提供，成品在另一端获取。

计算机必须在限定的时间内处理好所有的数据、做好响应。时间一旦对不上就可能会出错。

硬实时系统还需要在代码执行之前预估所需时间，要求即使遇到最坏情况也能在 ddl 之前完成。软实时系统的要求就没那么严格。

如果在实时系统上面抢占式的运行进程，还要满足进程切换尽量快，要不然也可能出事儿。

有一些专门应用于实时系统的调度算法，比如：

最早 ddl 优先，用一个优先队列存储 ready 的进程，最急迫的在最前面
最小松弛算法 Least Laxity Algorithm，就是说一个进程假设至少需要 $t_1$ 时间，不能超过 $t_2$ 时间，那么就按照松弛时间 $t_2-t_1$ 排序，选取松弛时间最小的。这个算法在非周期性的情况下表现得挺不错。