Lecture 7. 贪心算法

贪心的原理

贪心算法就是在每一步做选择的时候，都选取局部最优解；贪心算法认为，这样可以导致最终得到全局最优解。

有些最优化问题，可以使用贪心算法。但依然存在许多问题，担心算法给出的解不是全局最优解。

贪心的步骤

确定问题的最优子结构
设计一个递归的算法
证明：如果贪心的进行选择，那么剩下的子问题只会有一个
证明：贪心的选择是安全的
设计一个贪心算法的递归实现
把递归实现改成迭代实现

贪心 vs 动规

动规每一步的选择通常取决于子问题，而贪心每一步的选择不会考虑子问题，只考虑局部
动规通常自下而上，贪心自上而下，不断减小问题规模

有些看起来很相似的最优化问题，可能有的能用贪心，有的不能用贪心。比如分数背包问题可以用贪心，零一背包不行。

哈夫曼编码

使用哈夫曼编码压缩数据，通常可以节省 20%~90% 的空间。

哈夫曼编码是根据字符出现的频率来构造字符的编码的。频率高的就分配一个短编码，频率低的就分配一个长编码。与定长编码相比，变长编码显然可以达到更好的压缩率。

无前缀码 prefix code

也有的文献当中将其译作「前缀码」。意思就是 没有任何字符的编码，是其他字符编码的前缀。可以证明，无前缀码可以保证达到最优数据压缩率。

无前缀码的一大优点，就是 没有歧义，解码结果一定唯一。在解码的时候可以直接扫描，遇到匹配的就匹配，然后继续解码后面的内容。

编码树

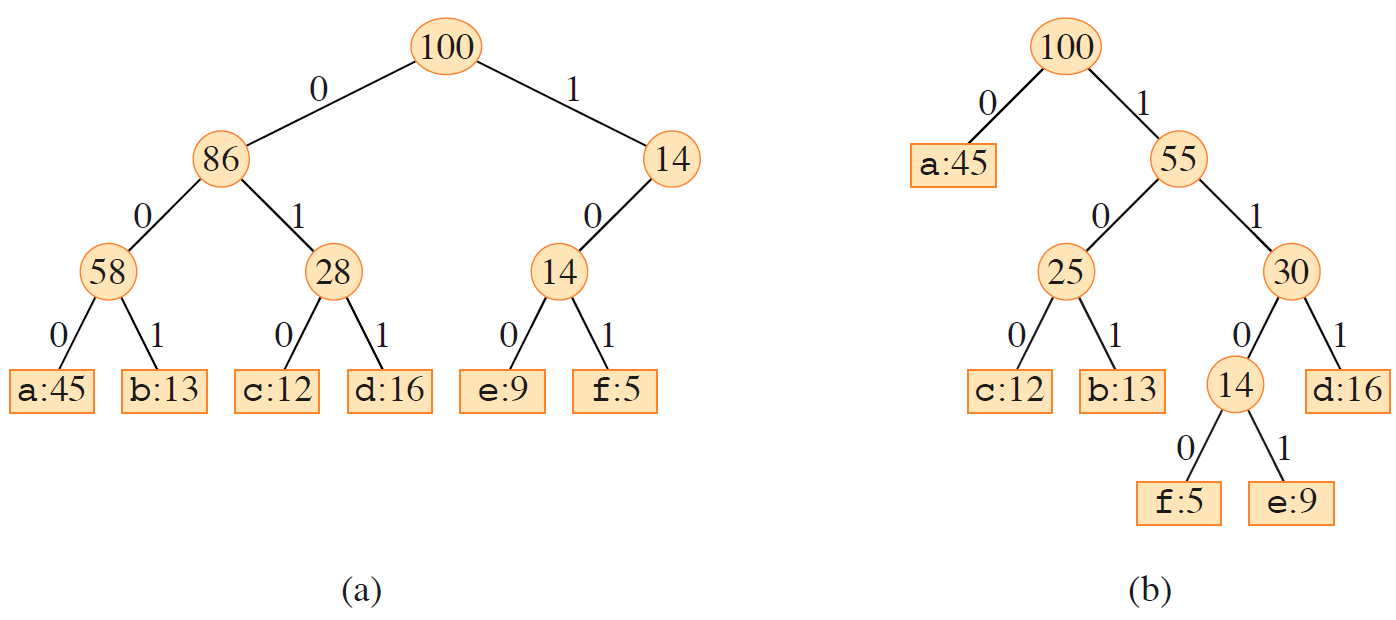
如图所示的二叉树叫做编码树，普通节点表示子树内所有字符的频率和，叶子节点表示字符及其频率。字符的编码是从根节点到自身的路径上字符的拼接。

对于所有的路径，遇到 0 向左，遇到 1 向右。

左边那个是定长编码的编码树，右边那个是哈夫曼编码的编码树（哈夫曼树）。

可以证明，最优编码方案：

一定对应着一棵 满（full）二叉树，即所有的非叶节点都必须有两个子节点。
设 $C$ 是字母表，则树中一定有恰好 $|C|$ 个叶子节点和 $|C|-1$ 个非叶节点

设 $d_T(c)$ 表示字符 $c$ 在这个编码树当中对应叶子节点的深度，这个深度等价于它的编码的长度。那么对于整个文件，使用编码树 $T$ 编码所需要的二进制位数就是 $$B(T) = \sum_{c\in C}c.freq \cdot d_T(c)$$。

哈夫曼树的构造

构造哈夫曼编码，要先构造哈夫曼树。如下代码使用给定字符集 $C$（包含字符及其频率）构造一个哈夫曼树。

这个哈夫曼树是 从叶子节点开始构造的，执行 $|C|-1$ 次合并操作，最终构造出哈夫曼树。代码当中，$Q$ 是一个以频率为关键字的优先队列，每次选取频率最低的两个进行合并，然后再插入回去（这不就是合并果子吗）。

如图体现了这个哈夫曼树的构造过程。

有了哈夫曼树就可以得到每个字符的编码了。

课件当中并没有讲哈夫曼编码正确性的证明。

哈夫曼编码构造方案的时间复杂度分析

假设优先队列是使用二叉堆实现的。

注意构造二叉堆需要的时间复杂度与从零插入所有元素的时间复杂度不同。构造仅需 $O(n)$ 时间。

然后提取优先队列当中最小元素相当于提取堆头，$O(1)$；但是插入是 $O(\lg n)$ 的。

一共进行了 $n-1$ 次操作，故总时间复杂度 $O(n + n \lg n) = O(n \lg n)$。

最小生成树

生成树

对于一个图 $G = (V,E)$，$V$ 的一个无环子集 $T$，能够将所有的节点连接起来，那么这个 $T$ 就一定是一棵树，叫做图 $G$ 的生成树。

说白了就是从具有 $n$ 个节点的图当中选取 $n-1$ 条边把所有节点连接起来所形成的树，

假设 $V$ 当中的边是带权的，边 $(u,v)$ 的权是 $w(u,v)$，那么生成树 $T$ 的权就是 $w(T) = \sum_{(u,v)\in T}w(u,v)$；权最小的生成树就叫做最小生成树。

求解最小生成树常用的有 Kruskal 算法和 Prim 算法，二者都是基于贪心的思想，且二者的时间复杂度都是 $O(E \lg V)$，注意不是 $O(V \lg E)$。

对于 Prim 算法，如果使用斐波那契堆进行优化，可以达到 $O(E + V \lg V)$ 的复杂度。

生成树算法的概括性描述

初始化一个空的边集 $A$
循环，如果 $A$ 暂时没有构成一棵生成树，那么就往里面加入一条 safe 的边（个人理解是要保证加入后不成环）
最终 $A$ 就是一棵生成树

Kruskal 与 Prim 算法的区别就在于 safe 的边的选择。

Kruskal 维持 $A$ 是一个森林，每次加入 $A$ 的新边都是权重最小的连接两个连通块的边
Prim 当中集合 $A$ 是一棵树，每次加入 $A$ 的新边都是连接 $A$ 和 $V-A$ 的权重最小的边

概念补充：割

定义无向图 $G=(V,E)$ 的一个 割（cut） $(S,V-S)$ 是集合 $V$ 的一个划分
如果一条边 $(u,v)\in E$ 的一个顶点位于 $S$ 中，另一个顶点位于 $V-S$ 中，就称这条边 横跨（cross） 了这个割 $(S,V-S)$
如果一个集合 $A$ 当中，不存在横跨这个割的边，那么就说这个割 尊重（respect） 集合 $A$
这个语境下，在横跨一个割的所有边当中，权最小的边，称作 轻边（light edge）（可能不唯一）

看图会比较好理解：红线把这个无向图分成了两块；这个割尊重蓝色边构成的集合；$(c,d)$ 是轻边。

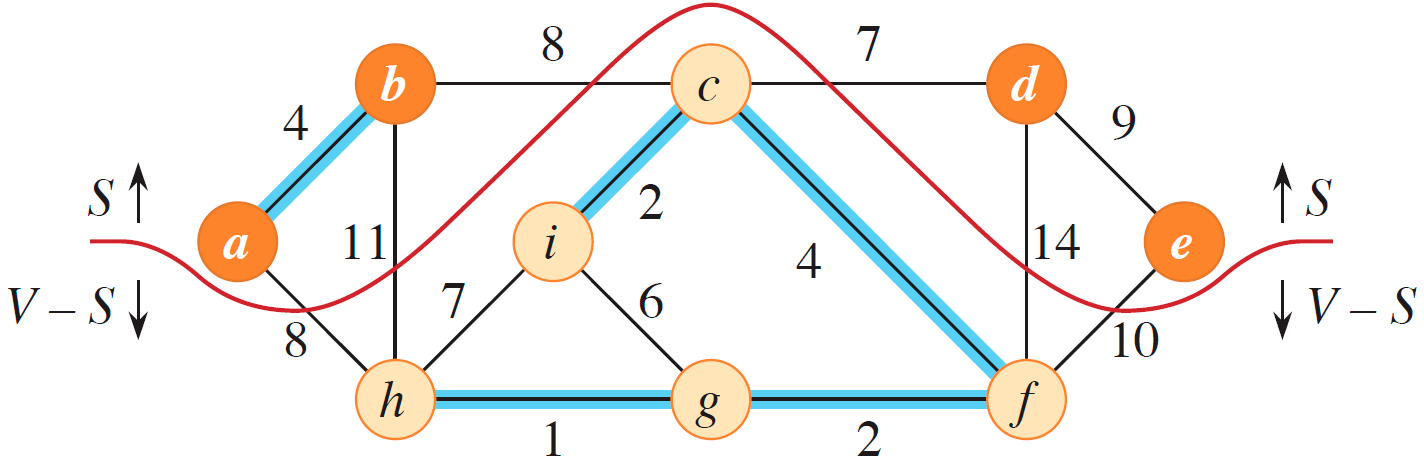
如何选择 safe 的边

设 $G=(V,E)$ 是一个连通的无向带权图，$A$ 是 $G$ 的某个最小生成树的边集的子集。设割 $(S,V-S)$ 是尊重 $A$ 的，且 $(u,v)$ 是横跨 $(S,V-S)$ 的一条轻边，那么这个 $(u,v)$ 对于集合 $A$ 来说就是安全的，可以加入。

具体证明没讲。在书上。

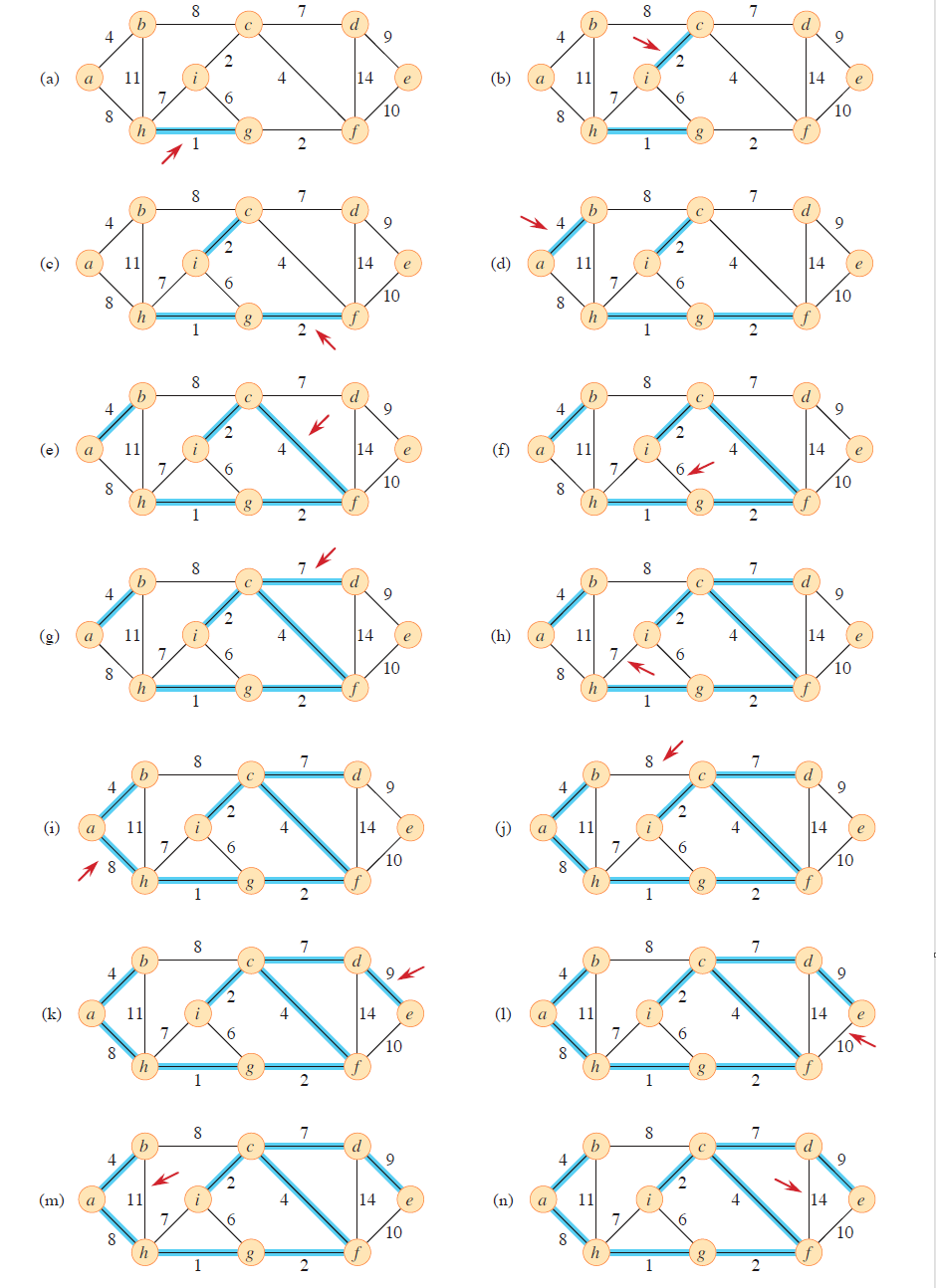
Kruskal 算法

伪代码

先对所有边排序，然后利用并查集检查是否在同一个连通块。

这里的并查集同时使用了路径压缩和按秩合并，因此每次操作的时间复杂度是反阿克曼函数级别.

图解

性能分析

最开始的排序需要时间 $O(E\lg E)$
并查集的操作执行了 $O(V+E)$ 次，贡献时间 $O(\alpha(V)(V+E))$，由于 $|E|\geq|V|-1$，式子化为 $O(\alpha(V)E)$
于是总时间 $O(E(\lg E + \alpha(V)))$，由于 $\alpha(V) = O(\lg V) = O(\lg E)$，化为 $O(E \lg E)$
由于边的数量最多是点的数量的平方，所以 $\lg |E| = O(\lg V)$，最终复杂度表示为 $O(E \lg V)$

Prim 算法

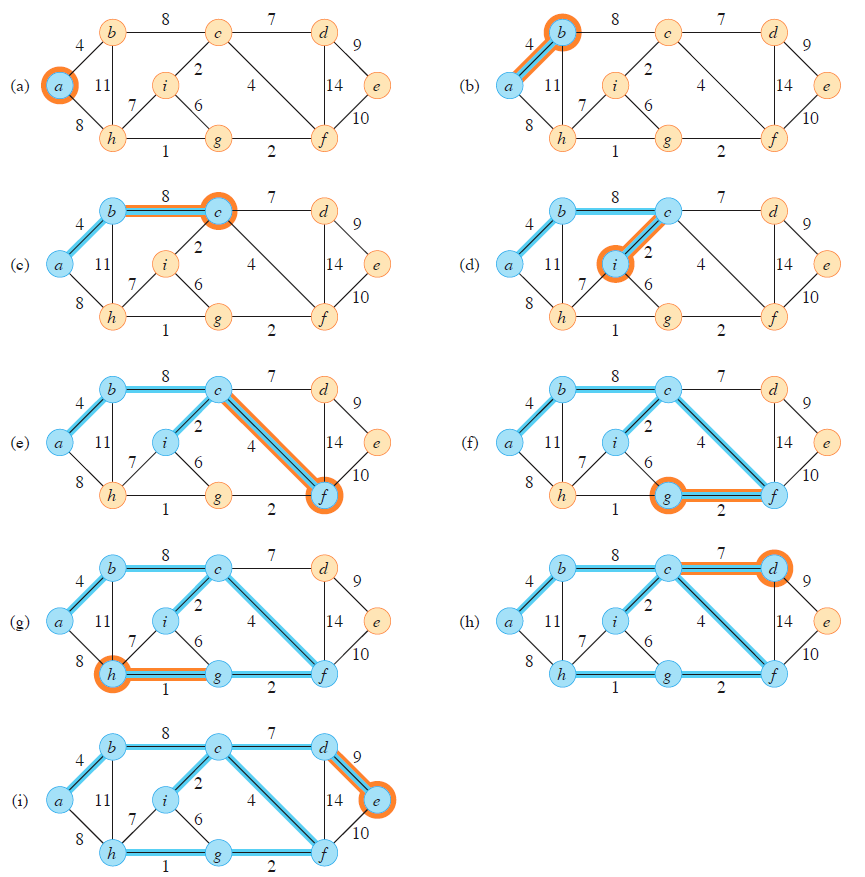
图解

初始的根节点随便选择一个就行，那就 a 号吧。

然后不停的从连接 $A$ 到 $V-A$ 边当中，找最短的那一条。因此需要数据结构（比如二叉堆/优先队列/斐波那契堆）来维护。

伪代码

这份伪代码使用一个功能很强大的优先队列来维护。其中 $u.\pi$ 是指节点 $u$ 在树当中的的父节点，$u.key$ 是给优先队列用于排序的键。

对于节点 $v$，$v.key$ 表示的是，能把 $v$ 连接到当前树的最小的边权。由于最开始还没有树，所以为了方便，先初始化为无穷。

第一个选择的节点是 $r$。

后面那个 for 有点类似 Dijkstra 或者 DP 的感觉，作用是更新其他非树节点的键值。不太好理解。

循环不变式

略

性能分析

Prim 算法的性能主要取决于优先队列的实现方式。这里的优先队列支持查找和修改键，不是普通的二叉堆。

那么构造这个优先队列耗时 $O(V)$
提取队首是 $O(\lg V)$ 的，执行了 $|V|-1$ 次，因此提取的总耗时应当是 $O(V \lg V)$
里面那一层 for 循环配上外面的 while，一共执行了了 $O(E)$ 次（因为是遍历邻接表），然后里面有一个 $O(\lg V)$ 的对优先队列的操作。因此这个循环耗时 $O(E \lg V)$
因此总共耗时 $O(V + V\lg V + E\lg V) = O(E+ E\lg E + E \lg V) = O(E \lg V)$