Lecture 6. 动态规划
为贪心而设的门紧锁着,为爆搜而开的洞敞开着,一个声音高叫着:用动规吧,给你满分!
动规基本原理
分治 vs 动规
分治是把一个大问题,分解成若干个 disjoint 互不相交的子问题,然后递归求解子问题,再把子问题合并成原问题的解。
对于子问题重叠(overlap)的情况,即子问题和子问题中间有共同的子子问题。这种情况下如果使用分治,就会重复计算;
动态规划,对于每一个子子问题,只求解一次,然后将结果保存到一个表格里。再次需要这个子子问题的时候,查表即可,无需重复计算(记忆化 memorization)。
通常动态规划用来求解 最优化问题(optimization problem),就是说找到一堆可行解当中的最优解。实际上最优解可能不仅有一个,动态规划方法找到一个即可。
动规的步骤
- 刻画(characterize)一个最优解的结构特征
- 递归地定义最优解的值
- 计算出最优解的值(通常是自底向上)
- (可选)利用前三步计算的信息,把最优解的方案构造出来
什么时候用动规
适合使用动规求解的最优化问题,应当具备两个基本性质:最优子结构、重叠子问题。
动规的时间复杂度
对于不同的问题,时间复杂度不尽相同,取决于两个因素
- 有多少个子问题
- 对于每个子问题,要考察多少个不同选择
最优子结构 optimal sub-structure
一个问题的最优解,包含其子问题的最优解,这就是「最优子结构」
如果某个问题具有最优子结构的性质,那么他可能就可以用动规求解。
动规的第一步:刻画最优子结构。那么如何发掘最优子结构?
- 需要证明:问题的最优解的第一个组成部分是,做出一个选择。这个选择会产生一个或多个子问题,比如背包问题。
- 假定在第一步的选择当中,已经知道了哪种选择可以得到最优解(并不关心该如何选,只是假定能知道哪个是)
- 做出选择后,确定出这个选择会产生哪些子问题,以及如何最好的刻画子问题空间
- 利用 cut-and-paste 方法证明,这个问题的最优解当中子问题的解,对于子问题而言,也是最优解。
- 可以用反证法证明。假设最优解当中子问题的解不是最优解
- 然后把子问题的解「剪贴粘贴」改成最优解
- 然后发现原问题的解变地更好了,形成矛盾
对于不同的问题,可能还会有两点不同:
- 原问题的最优解,涉及到的最优子结构的个数
- 确定最优解包含哪些子问题的时候,可以选择的个数
一般在代码实现当中,会使用自底向上的方法,来利用最优子结构。说白了就是,得到子问题的最优解,从而得到原问题的最优解。原问题的解的值,一般就是子问题的解的值,加上选择所产生的值。
重叠子问题 overlapping sub-problem
就是说一个问题的递归算法,总是在反复求解某些相同的问题,而没有不断生成新的子问题。也就是说子问题的空间应当是足够小的,最好是多项式等级的。这就叫「重叠子问题」性质。
于是可以用记忆化(查表)的方式快速得到某个已经计算过的问题的解。
例:最长公共子序列问题
用四个步骤来算出最长公共子序列。
第一步:刻画 LCS
定义:
- 长度为 $m$ 的字符串 $X = \langle x_1, x_2, \cdots, x_m \rangle$
- $X_i = \langle x_1, x_2, \cdots, x_i \rangle$ 是 $X$ 的第 $i$ 个前缀
- 长度为 $n$ 的字符串 $Y$ 及其 $n$ 个前缀同理
则显然满足以下三点性质(详细证明在书上):
- 若 $x_m = y_n$ 即 $X$ 与 $Y$ 的最后一个字符相等,则 $z_k = x_m = y_n$ 且 $Z_{k-1}$ 是 $X_{m-1}$ 和 $Y_{n-1}$ 的一个 LCS,减小原问题的规模
- 若 $x_m \ne y_n$ 即 $X$ 与 $Y$ 的最后一个字符不相等,那么 $z_k \ne x_m$ 就意味着 $Z$ 是 $X_{m-1}$ 和 $Y$ 的一个 LCS,即假如 LCS 的最后一个字符与 $X$ 的最后一个字符不同,就可以当作 $X_{m-1}$ 和 $Y$ 的 LCS 问题,减小规模
- 若 $x_m \ne y_n$ 即 $X$ 与 $Y$ 的最后一个字符不相等,那么 $z_k \ne y_n$ 就意味着 $Z$ 是 $X$ 和 $Y_{n-1}$ 的一个 LCS,即假如 LCS 的最后一个字符与 $Y$ 的最后一个字符不同,就可以当作 $X$ 和 $Y_{n-1}$ 的 LCS 问题,减小规模
简单总结来说就是:两个字符串的 LCS 会包含两个字符串的前缀的 LCS,因此 LCS 问题具有最优子结构性质。
第二步:递归解
根据上述性质,求解 LCS 问题的时候,要分两类情况讨论
- 一个情况是 $x_m = y_n$,直接转化为 $X_{m-1}$ 和 $Y_{n-1}$ 的 LCS 问题
- 另一情况是 $x_m \ne y_n$,则求 $X_{m-1}$ 与 $Y$ 的一个 LCS,再求 $X$ 与 $Y_{n-1}$ 的一个 LCS,取两个当中长的那个
由于这样分类讨论可以覆盖所有的可能情况,所以必然有一个子问题的最优解,出现在原问题的最优解($X$ 与 $Y$ 的 LCS)当中。
然后 $X_{m-1}$ 与 $Y$ 的子问题当中可能包含 $X_{m-1}$ 与 $Y_{n-1}$ 的 LCS 问题,这就产生好多重叠。
最后列出状态转移方程。令 $c[i,j]$ 表示 $X_i$ 与 $Y_j$ 的 LCS 的长度:
$$c[i,j] = \begin{cases}0 & i=0\text{ 或 }j=0 \\ c[i-1,j-1]+1 & i,j>0\text{ 且 }x_i=y_j \\ \max(c[i,j-1],c[i-1,j]) & i,j>0\text{ 且 }x_i \ne y_j\end{cases}$$
第三步:算出 LCS 的长度是多少
所有子问题的规模总和,即 $c[i,j]$ 的大小,是 $\Theta(mn)$,于是可以自底向上递归计算。
由于每一个 $c[i,j]$ 都是 $\Theta(1)$ 计算的,所以这个函数的时间复杂度也是 $\Theta(nm)$。

第四步:构造出一个 LCS
在计算 $c[i,j]$ 的同时,维护了一个 $b$,$b[i,j]$ 表示的是计算 $c[i,j]$ 的时候,选择了哪一个子问题的最优解,取值只有三种:左、上、左上。
然后根据 $b$ 的信息,把所有 ↖ 箭头对应的 $i,j$ 拿出来($x_i=y_j$ 一定满足),就可以构造出来一个 LCS,如图所示。
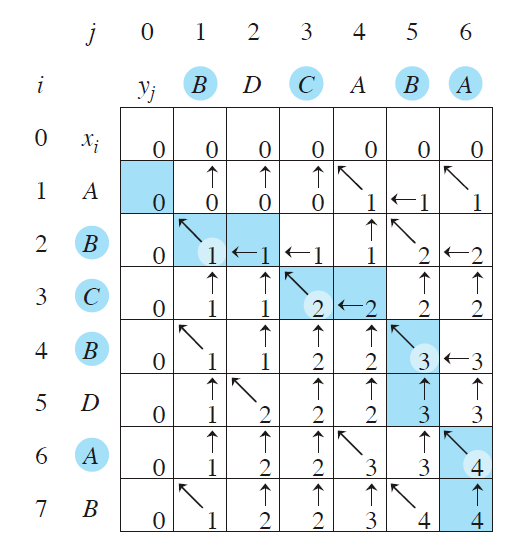
对应到代码,就是从右下角开始一直根据箭头方向走,时间复杂度 $O(m+n)$。

算法的改进
其实 $b$ 是不需要的,因为 $b[i,j]$ 可以根据 $c$ 算出来,所以 $b$ 数组可以省略。
但是由于 $c$ 数组是必须的,所以空间复杂度仍然是 $\Theta(mn)$ 没啥变化。
然而如果不需要构造 LCS 只想知道长度的话,可以利用滚动数组之类的思想,减少 $c$ 的空间使用。