Lecture 4. 树

二叉搜索树 Binary Search Tree

搜索树是一种支持 search get-min get-max insert delete predecessor successor 等动态集合操作的数据结构。

搜索树可以当作字典，也可以当作优先队列。

二叉树三种递归遍历方式

由于二叉树每个节点最多拥有两个子节点，所以，二叉树有以下三种递归的遍历方式（还有非递归的层次遍历）

中序遍历：左根右（inorder）。BST 的中序遍历产生的序列是单调的！伪代码如下。
先序遍历：根左右（preorder）
后序遍历：左右根（postorder）

三种遍历方式都是 $\Theta(n)$ 的。

二叉树可以用链表实现。每个节点除了 key，还包含左右儿子和父节点（如果不存在则 NIL）。只有根节点的父节点是 NIL。

BST 性质

对于二叉搜索树，各种操作的效率与树高有关。对于完全二叉树，效率最坏 $\Theta(\lg n)$。但是最坏情况下树退化成一条链，复杂度变成最坏 $\Theta(n)$。

二叉搜索树当中，对于每个节点 $x$，设 $y \in x.l, z \in x.r$，都满足：$y.key \leq x.key \leq z.key$。也就是说，左子树当中所有节点都小于等于根，右子树当中所有节点都大于等于根。

此外，CLRS 当中认为根节点的深度是 0。 如下图，CLRS 认为这棵 BST 的高度是 $2$。

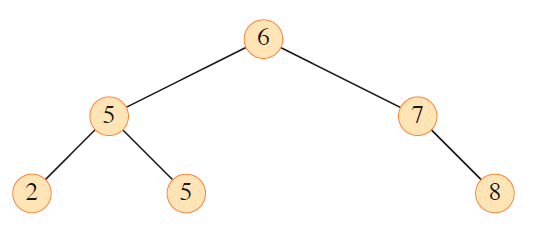
然而，根节点如果选取不当，则可能导致不平衡，树高增长到 $4$：

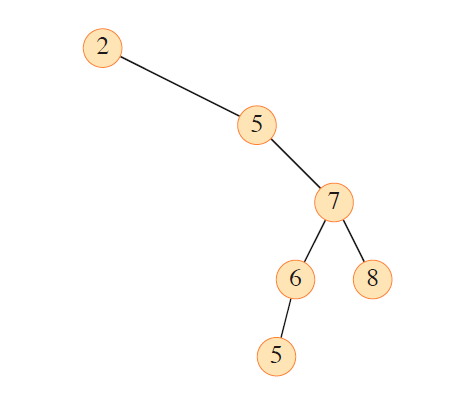
BST 的各项查找操作

查找指定元素

Search(x, k) 表示在根是 $x$ 的子树当中查找键值 $k$ 的元素的指针。效率 $O(h)$。

递归的版本比较好写，也可以写非递归的版本，常数小一些。以下是两种伪代码。

查找最大最小值

最大值就一路向右，最小值一路向左，效率 $O(h)$。

代码就一个 while：

查找前驱和后继

这里的前驱和后继，都是指 中序遍历 产生的序列上的前后相邻的节点。

中序遍历是「左根右」产生的，因此它单调。如果一棵 BST 当中所有的键值互不相同，那么一个节点的

前驱（predecessor）就是比他小的最大节点
后继（successor）就是比他大的最小节点

最简单的办法就是，执行中序遍历，把序列搞出来，然后再从这个序列里面线性或者二分的去找当且节点，然后得到前驱后继。但是这个效率太低了。

分析（以查找后继为例）

情况一：有右子树

如果这个节点具有右子树，那么它的后继结点，就是右子树当中的最小值。

直接调用 get-min(x.r) 即可获得后继。

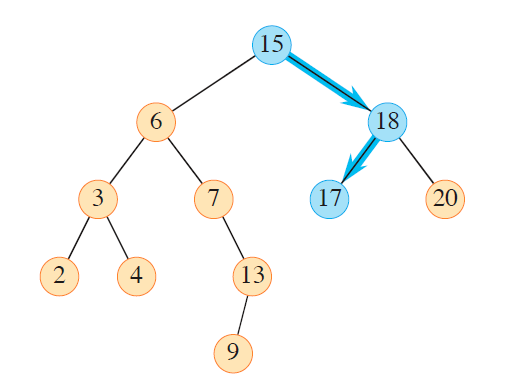
情况一：无右子树

如果这个节点不具有右子树，它仍有可能具有后继结点：

它如果是父节点的左儿子，那么它的父节点就会比他大。此时它的父节点就是后继。
如果它是父节点的右儿子，虽然它的父节点没它大，但是它的父节点可能属于它的太太太太太爷爷的左子树，于是它的父节点大不过它的太太太太太爷爷，从而有可能它的太太太太太爷爷比它大，是它的后继。

再结合中序遍历左根右的特性，这种情况下，$x$ 的后继是：位置最深的，左儿子是（$x$ 自己或 $x$ 的祖先）的 $x$ 的祖先。

如下图，从 $13$ 自底向上（寻找满足要求的深度最深的），它的所有祖先节点 $x$ 当中，第一个是 $x.fa$ 的左儿子的 $x$ 是 $x=6$。于是，$13$ 的后继就是 $6.fa = 15$。

伪代码

效率是 $O(h)$ 的。

YYF 感觉这个 else 用了个 y，反而画蛇添足不太好理解。不如改成：

TREE_SUCCESSOR(x)
1 if x.right != NIL
2   return TREE_MINIMUM(x.right)
3 else
4   while x.fa != NIL and x.fa.left != x
5     x = x.fa
6   return x.fa

BST 的插入与删除操作

插入和删除会影响原先 BST 的结构。需要保证插入或删除之后，树依然满足 BST 的性质。

插入操作比较简单（插到合适的叶子上，结构肯定没有影响），但是删除操作需要调整结构。

插入

插入的元素，一定会成为新的叶子。

示例

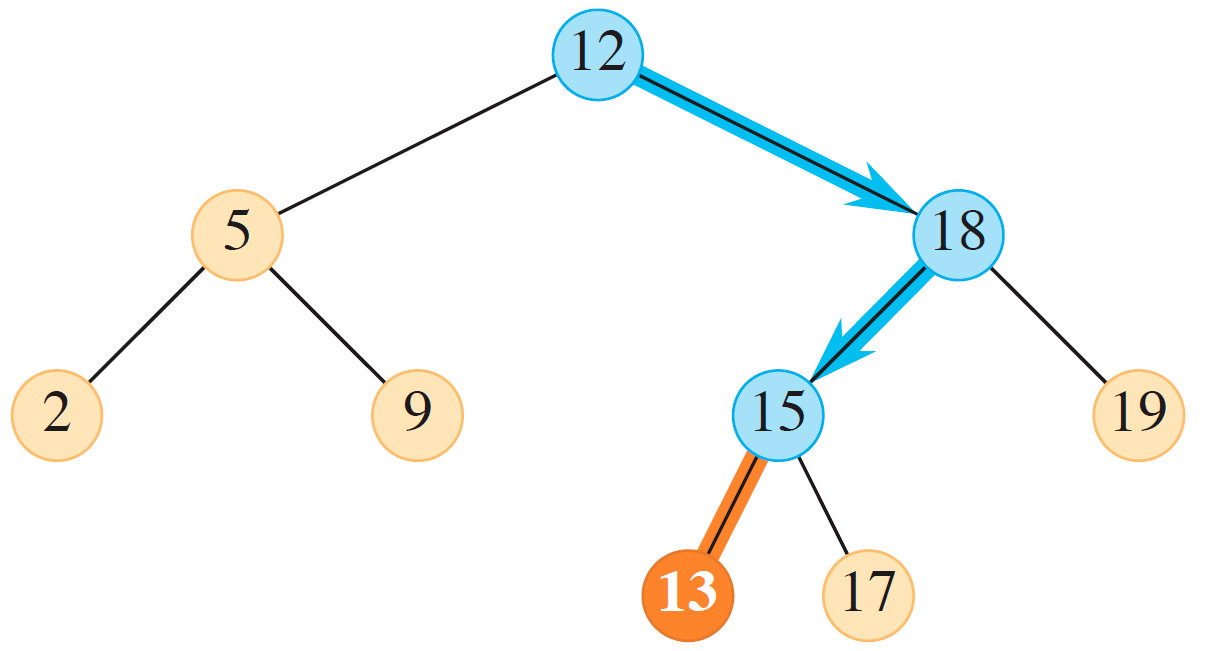
带有颜色的路径表示插入过程走过的路径。深橙色表示要插入的元素最终能够确定的位置。

插入的过程可以用递归的方式描述：

首先与根节点比较。$13>12$，因此现在移动到右子树。
再跟当前的根节点比较，$13<18$，移动到左子树。
再跟当前的根节点比较，$13<15$，还是移动到左子树。
再跟当前的根…欸，不对，现在这棵树是空的。那就插在这儿了！

效率 $O(h)$。

伪代码：将 $z$ 插入到 BST $T$ 中

然而，CLRS 当中给出的伪代码是非递归的，常数小一些：

以下代码用 $x$ 表示当前走到的节点（从根开始），不断更新
直到 $x = NIL$ 表示走到空树（递归边界），开始处理
$y$ 一直用于备份 $x$。因此，当 $x \leftarrow x.lr$ 后，$y$ 就是 $x.fa$
由于 $z$ 要插入到当前空树的位置，所以 $z.fa \leftarrow y$
由于 $z$ 是叶子，所以 $z.lr = NIL$（这在伪代码中没有体现，因为我们假设插入前的 $z$ 的各个指针都是 NIL）
最后用条件语句更新一下 $z.fa.lr$ 也就是 $y.lr$（判断 $z$ 是 $y$ 的左儿子还是右儿子）。对于特殊情况（树空，$y$ 不存在），把 $z$ 当作树根。

删除

删除操作有点麻烦，因为需要维护树的结构，保持 BST 的性质。

分析

删除节点有三种情况：

要删除的节点是叶子——那就直接删掉他，然后父亲丧子！
要删除的节点有一个孩子——那就把他删掉，孙子变成了爷爷的儿子！
要删除的节点有两个孩子——哎呀太麻烦了。不想学了。

每个要删除的节点 $z$，总共有五种可能的情况（00D、01D、10D、111、110）：

没左儿子（0XD)：
- 没右儿子（00D）
- 有右儿子（01D）
有左儿子（1XD）：
- 没右儿子（10D）
- 有右儿子（11X）
  - 右儿子是后继节点（111）
  - 右儿子不是后继节点（110）

方案：没左儿子、没右儿子（00D）

它是叶子。直接删掉。更新父亲的指针。

方案：没左儿子、有右儿子（01D）

用右儿子替换掉 $z$，更新父亲的指针。

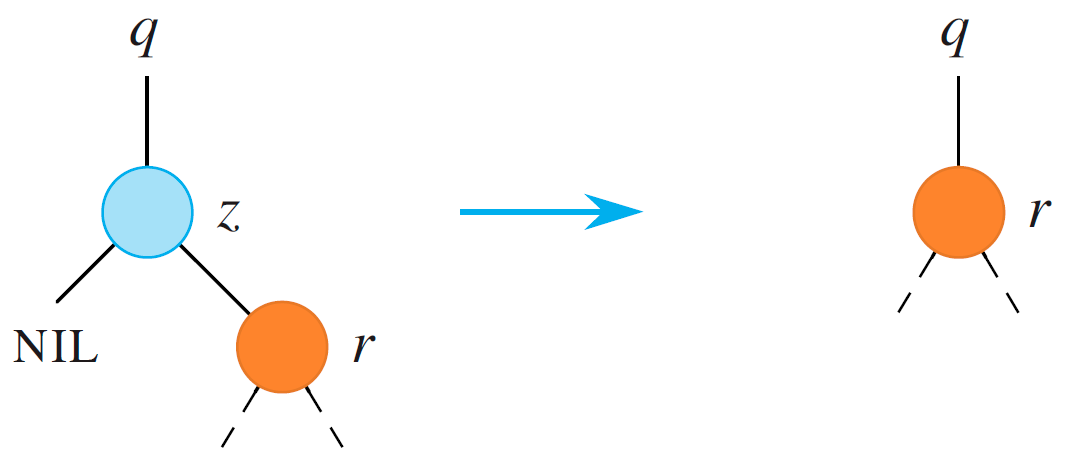
方案：有左儿子、没右儿子（10D）

用左儿子替换掉 $z$，更新父亲的指针。

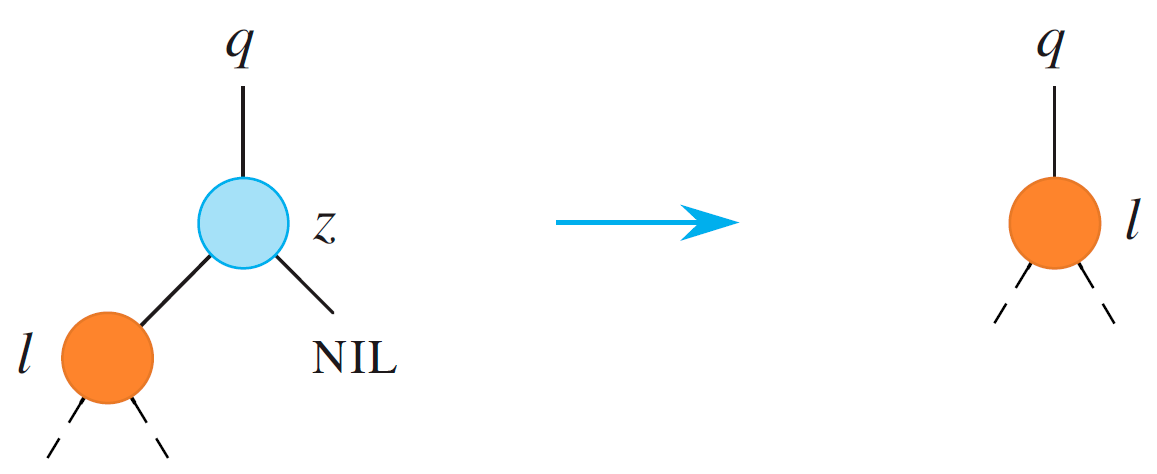
方案：有左儿子、有右儿子（11X）

考虑 $z$ 的后继节点 $y$。由于两个儿子都存在，所以 $y$ 一定在右子树当中。由中序遍历的性质可知，这个后继节点 $y$ 一定不会拥有左儿子，可能拥有右儿子。

如果后继 $y$ 不是 $z$ 的直接右儿子，就先 $y \leftarrow y.r$，然后 $z \leftarrow y$。
如果后继 $y$ 是 $z$ 的直接右儿子，就直接 $z \leftarrow y$。

总之，后继 $y$ 要变成新的根。

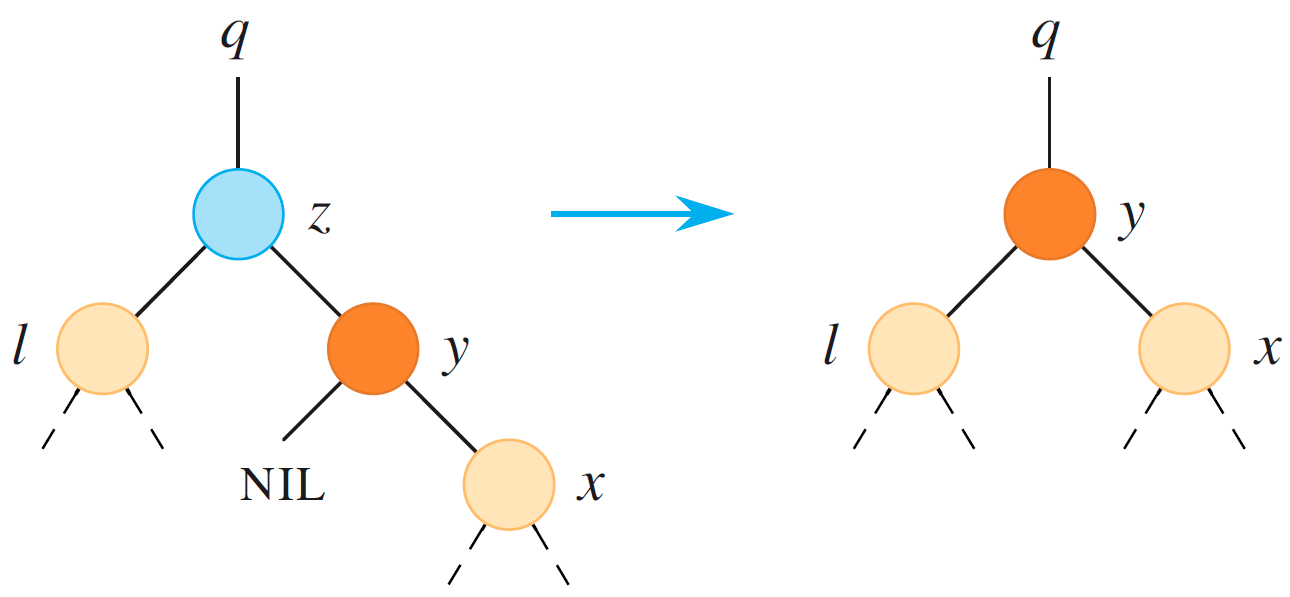
如果 $y$ 是 $z$ 的直接右儿子（111）

把 $z$ 的左儿子变成 $y$ 的左儿子（原本不存在），然后用 $y$ 替换 $z$。记得修改 $z$ 的父节点指针。

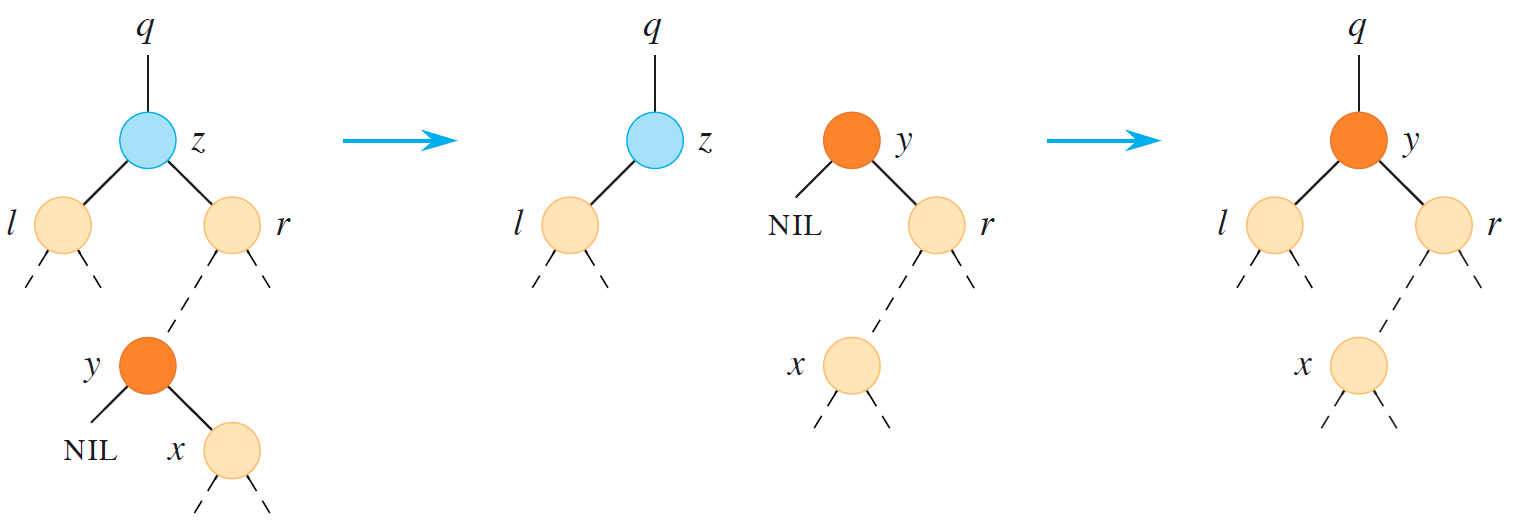
如果 $y$ 不是 $z$ 的直接右儿子（110）

最麻烦的一种情况。概括起来说，就是 $y$ 的右子树替换掉了 $y$，然后再用原先的节点 $y$ 替换节点 $z$；详细来说，就是（课件这个示意图太麻烦了，不要管他）：

从 $z$ 的右子树当中，删掉后继结点 $y$（它没左儿子，可能有右儿子，很好删）
从某个地方新建一个 $y$ 节点
把 $z$ 的右子树（以 $r$ 为根）抽出来，作为 $y$ 的右儿子（图中）
把原先 $z$ 的左子树（以 $l$ 为根）抽出来，作为 $y$ 的左儿子
此时 $z$ 已经是个叶子了。把以 $y$ 为根的子树替换掉节点 $z$（图右），结束。

伪代码：从树 $T$ 中删除节点 $z$

由于删除操作涉及到「子树移动」操作，所以需要一个 Transplant(T, u, v)，把以 $u$ 为根的子树，替换成以 $v$ 为根的子树。注意，这里的 $v$ 可以是空树。

移植操作的效率是 $O(1)$。

注意这里的指针修改只涉及 $u.p.left$ 或 $u.p.right$，并不包含 $v.left$ 与 $v.right$，因为 $v$ 的子树是一起移动过来的

然后是删除操作的伪代码，效率 $O(h)$：

注意，$y$ 本身是不可能有左儿子的。而 $y$ 替换掉 $z$ 之后就有左儿子了，所以执行 Transparent(T,z,y) 之后要更新一下 $y.left$ 的信息。类似地，$y.right$ 替换掉 $y$ 之后，新的 $y.right$ 也要做出相应的修改。

前两种情况只需要移植不需要手动修改其他指针。后两种（俩儿子）需要手动修改指针。

红黑树

BST 的各项操作都是 $O(h)$ 的，但最坏情况下一棵 BST 可能退化成链，那么每次操作就都是 $O(n)$ 的。

红黑树也是一种 BST，但可以避免退化成链。红黑树确保没有一条路径会比其他路径长出两倍，因而是近似于平衡的。因此红黑树的各项操作，时间复杂度都是 $O(h) = O(\lg n)$。

红黑树的每个节点，除了 $key$, $left$, $right$, $p$，还新增了一个 $color$。红黑树当中还有一个特殊的黑色哨兵（sentinel）节点 $T.nil$，表示根节点的父节点以及所有叶子节点，除了 $color$，它的其他四项属性可以等于任意值。这个哨兵节点对于红黑树的边界处理很方便。在红黑树的代码实现当中，所有的 NIL 都用 T.nil 替换。

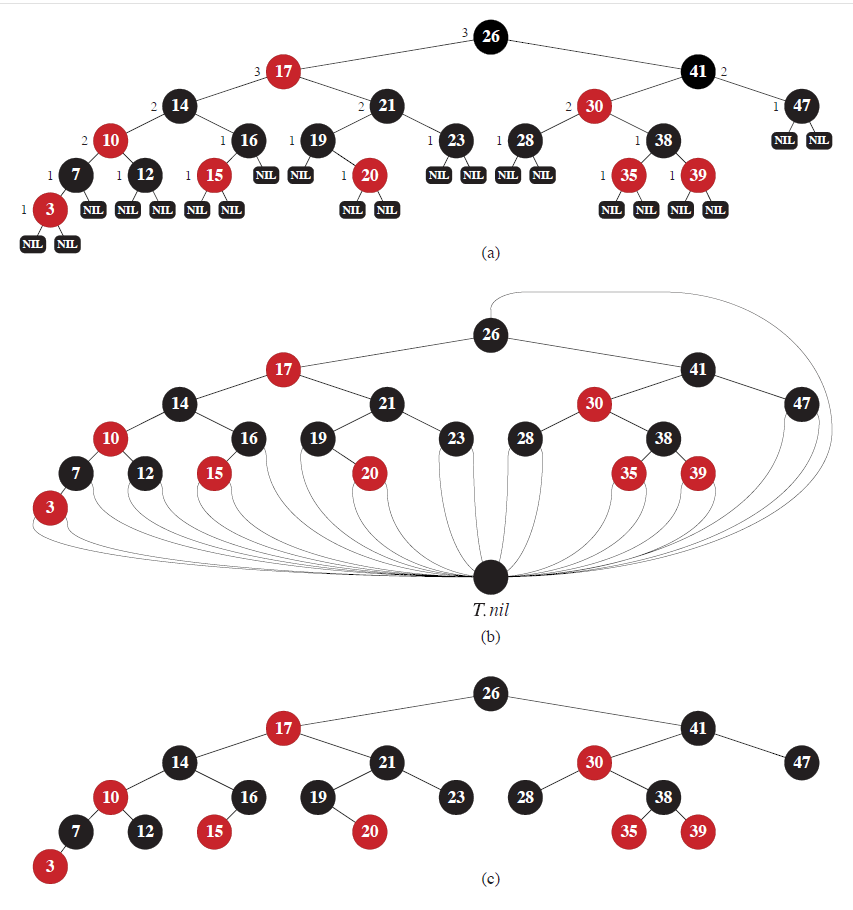
红黑树可以有三种表示方式。图一比较原始，图二把所有的 $NIL$ 替换成了 $T.nil$，图三省略了所有的哨兵，关注核心部分。

红黑树基本性质

红黑树除了满足 BST 的基本性质，还满足以下五条红黑性质：

每个节点都具有一个颜色，要么红色，要么黑色
根节点是黑色的
每个叶子节点（T.nil）是黑色的
如果一个节点是红色的，那么它的两个子节点，必须是黑色的
对于每一个节点，从它到子树中每个叶子节点的简单路径上，黑色节点的数量都相等

定义 黑高（black height） $\operatorname{bh}(x)$ 表示节点 $x$ 出发（不含），到任意一个叶子节点的简单路径上，黑色节点的个数。红黑树的黑高等于根节点的黑高。

证明：红黑树的高度不超过 $2\lg(n+1)$

首先证明：任意节点 $x$ 的子树中，至少包含 $2^{\operatorname{bh}(x)}-1$ 个非 nil 节点。当 $x$ 是叶子（nil），高度为 $0$，显然成立；再考虑高度非零的情况，它的子节点的黑高要么是 $\operatorname{bh}(x)$ 要么是 $\operatorname{bh}(x)-1$。注意，由于红黑树的叶子 nil 是填满了所有位置的，所以每一个节点高度非零的节点都一定有且仅有两个子节点。所以每个 $x$ 的子节点的子树当中，至少包含 $2^{\operatorname{bh}(x)-1}-1$ 个非 nil 节点，于是 $x$ 的子树当中包含的非 nil 节点的个数就至少是 $2 \times \left(2^{\operatorname{bh}(x)-1}-1\right) + 1 = 2^{\operatorname{bh}(x)}-1$。

设整棵红黑树的高度（根节点的高度）是 $h$。根据性质四，从根节点到任意叶节点的简单路径（不包含根本身）上，至少有一半是黑色节点，即 $\operatorname{bh}(T.root) \geq \frac{h}{2}$。而根节点的子树当中非 nil 节点的个数恰好是 $n$，也就是说，$n \geq 2^\frac{h}{2}-1$。

上面这个式子移项再取对数，可得 $\lg(n+1) \geq \frac{h}{2}$，即 $h \leq 2\lg(n+1)$。

因此红黑树的各项查找操作（只读）的时间复杂度都是 $O(h) = O(\lg n)$。对于插入和删除其实也是 $O(\lg n)$ 的，但是麻烦一点，后面再说。

旋转 rotation

研究红黑树的插入和删除之前，先研究一下，BST 的旋转操作。

旋转分为左旋右旋，且操作之后仍然保持 BST 性质，如图。

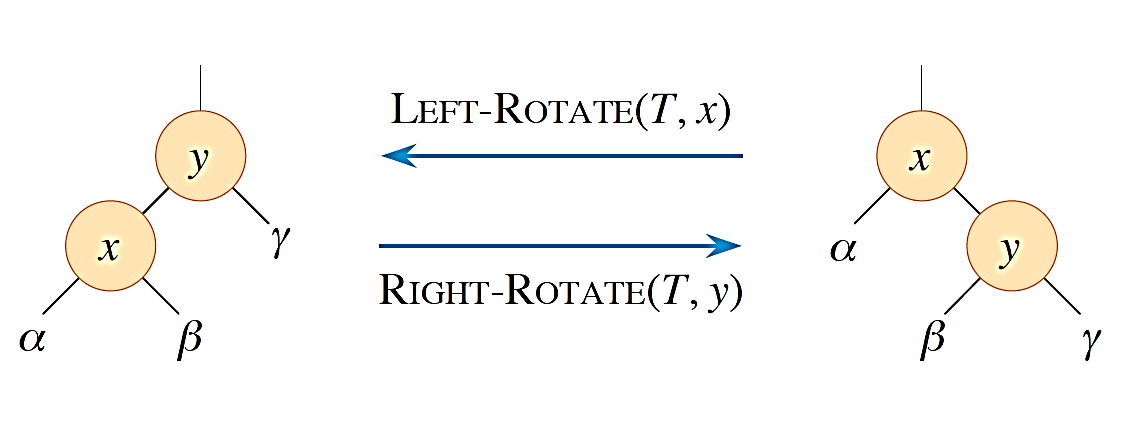
左旋就是把当前根节点 $x$ 的右子节点（非 nil），旋到上面去。右旋就是把当前根节点 $y$ 的左子节点 $x$（非 nil），旋到上面去。

对于左旋

把 $x$ 的右子树换成 $y$ 的左子树，随后视情况更新 $y.left.p$
把 $y.p$ 换成 $x.p$，随后视情况更新 $x.p.left$ 或 $x.p.right$ 或 $T.root$
$x.p$ 更新为 $y$，同时 $x$ 成为 $y.left$

对于右旋

把 $y$ 的左子树替换成 $x$ 的右子树，随后视情况更新 $x.right.p$
把 $x.p$ 换成 $y.p$，随后视情况更新 $y.p.left$ 或 $y.p.right$ 或 $T.root$
$y.p$ 更新为 $x$，同时 $y$ 成为 $x.right$

代码跟左旋是对称的（呼唤所有的 x、y 以及 left、right），这里就不放了。

旋转操作的性能

由于只涉及到指针的修改，所以是 $O(1)$ 的。

插入

红黑树的插入操作 RB-INSERT(T, z 与 BST 的插入非常类似：

所有的 NIL 改成了 T.nil
给新插入的节点新增了两个 T.nil 作为叶子
把插入的节点的颜色弄成红色
为了维持红黑树的性质，最后调用了一个 RB-INSERT-FIXUP

那么，主要研究的问题就是，红黑树的性质可能会因为什么而遭到破坏？

修复红黑性质

由于插入的是红色节点，黑高一定不会受到影响。那么唯一可能影响红黑性质的情况就是，插入的节点的父节点也是红色（代码当中体现为 while (z.p.color == RED) {}）。

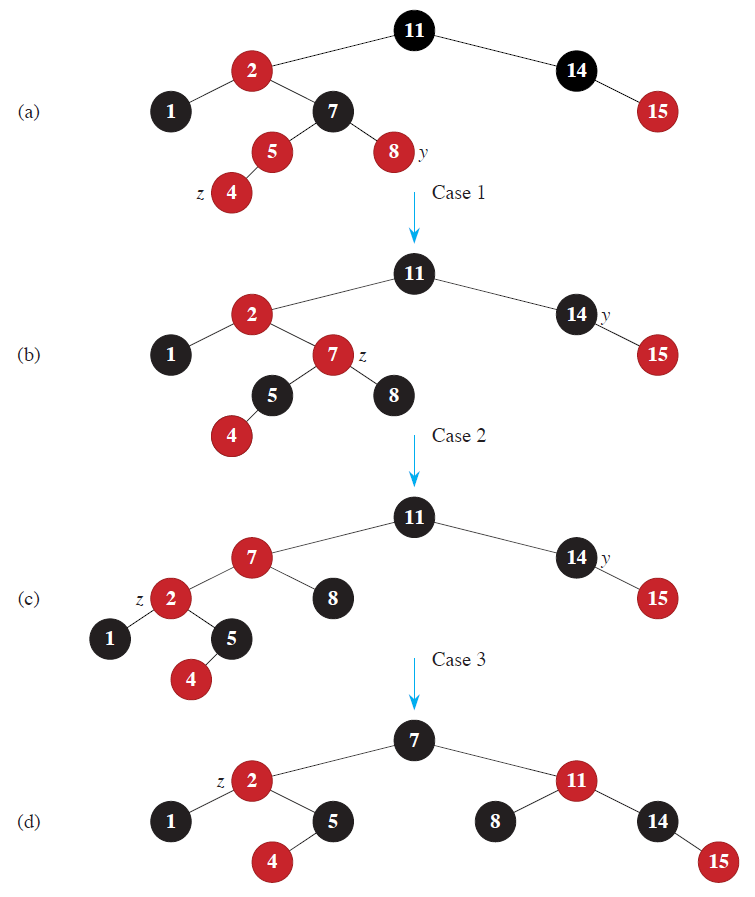
看图研究。

以开始刚把 $z$ 插入进去，它和爹都是红的，不行。他爹是他爷爷的左子节点，他叔叔是他爷爷的右子节点。他叔叔竟然也是红的。这时候（爹跟叔叔都是红的）就应用代码的 case 1：爹跟叔叔都改成黑的，爷爷改成红的。然后 $z=z.p.p$ 跳上去两格
现在的 $z$ 跟他爹又都是红的，还得继续修！不过这时候他叔叔是黑的了。这时候（爹红叔叔黑，自己是爹的右孩子），应用代码的 case 2：先 $z=z.p$ 跳一格，然后对 $z$ 左旋，然后（这时候 $z$ 已经变了）爹改成黑色，爷爷改成红色，再给爷爷执行右旋
现在的 $z$ 跟他爹依然都是红的，又要继续修！现在（爹红叔叔黑，自己是爹的左孩子），只需要爹改黑，爷爷改红，然后爷爷右旋
过程中可能把根作为爷爷给改成红色了，那最后再赋回黑色就好了

修复的代码

代码前半段与后半段高度对称（所有 left、right 互换）

插入操作的性能

首先 RB-INSERT 的前半部分跟之前 BST 的插入没什么变化，所以是 $O(h)=O(\lg n)$ 的。那么主要分析修复过程的效率。

对于 case 1，由于每次循环后都执行 $z = z.p.p$，所以 case 1 执行循环次数最多是 $O(h)=O(\lg n)$ 级别的。
一旦执行了 case 2 或者 case 3 的代码，由于把爹改成黑的了，所以循环会就此终止。
因此修复过程也是 $O(\lg n)$ 的。

因此，红黑树的插入操作是 $O(\lg n)$ 的。

删除

不考。