Lecture 2. Divide and Conquer 分治

分治算法的核心步骤是：

分 divide。把当前问题分成子问题。
治 conquer。递归的解决子问题。当问题规模足够小（递归边界）就直接解决。
合并 combine。根据子问题的答案，计算出当前问题的答案。

归并排序 Merge Sort

归并排序是分治算法的典型例子。归并排序是 bottom-out（触底反弹，也可以理解为自底向上）的，其中，底是指当前序列长度为 $1$ 的情况。

归并排序的三个分治步骤是：

分解 divide：将原数组对半分成子数组
解决 conquer：递归，对两个子数组进行归并排序
合并 combine：把两个有序的子数组合并成一个新的有序的数组

归并排序的核心： `MERGE`

归并排序的核心，是「合并」步骤，也就是把两个已经排序好了的子数组合并成一个新的有序数组。这个合并过程需要 $\Theta(n)$ 的时间。MERGE(A, p, q, r) 实现合并 $A[p .. q]$ 和 $A[q + 1.. r]$ 的过程。

MERGE 的原理是，先把两个有序子数组提取出来，然后设立两个指针，边比较大小边移动。最后处理剩下的部分。

YYF 的版本

YYF 觉得 CLRS 写的这个太丑了，于是用 Java 重新实现了一个

public static void merge(int[] a, int p, int q, int r) {
    int nl = q - p + 1, nr = r - q;
    int L[] = new int[nl], R[] = new int[nr];
    for (int i = 0; i < nl; ++i)
        L[i] = a[p + i];
    for (int j = 0; j < nr; ++j)
        R[j] = a[q + j + 1];
    int i = 0, j = 0, k = p;
    while (i < nl && j < nr)
        if (L[i] <= R[j])
            a[k++] = L[i++];
        else
            a[k++] = R[j++];
    while (i < nl)
        a[k++] = L[i++];
    while (j < nr)
        a[k++] = R[j++];
}

归并排序性能分析

要分析归并排序的性能，先要分析 MERGE 的性能。显然一次 MERGE 是 $\Theta(n)$ 的（这个 $n$ 其实是 $r-p+1$），因为指针 $i$ 和 $j$ 总共移动的距离之和恰好是 $r-p+1$。

由于归并排序的实现是涉及到递归的，所以在分析复杂度的时候也可以列出递归的式子。

设 $T(n)$ 表示解决原问题所需要的时间。当 $n$ 足够小，无需分治，此时只需要常数时间，即 $\Theta(1)$；当需要分治的时候，设原问题可以被拆解为 $a$ 个子问题，每个子问题的规模是原问题的 $\frac{1}{b}$，那么就需要解决 $a$ 个规模为 $\frac{n}{b}$ 的问题，再设将原问题拆开所需要的时间是 $D(n)$，合并子问题答案所需时间是 $C(n)$，那么：$$T(n)= \begin{cases}\Theta(1) & \text { if } n<n_0 \\ D(n)+a T(\frac{n}{b})+C(n) & \text { otherwise }\end{cases}$$。对于归并排序，$a=b=2$，于是 $aT(\frac{n}{b}) = 2T(\frac{n}{2})$。（注意：归并排序当中 $a=b=2$，但是有一些分治算法当中 $a\not= b$）

接下来分析一下 $D(n)$ 和 $C(n)$：

由于拆分问题只是需要计算一下中点的位置，所以是 $D(n) = \Theta(1)$
$C(n)$ 就是 MERGE 所需要的时间，所以 $C(n) = \Theta(n)$

于是，得到 $$T(n)= \begin{cases}\Theta(1) & \text { if } n=1 \\ 2T(\frac{n}{2}) + \Theta(n) & \text { otherwise }\end{cases}$$，其实 $T(n) = \Theta(n \lg n)$，这个可以用主定理证明。接下来用图示的方式解释为何是 $\Theta(n \lg n)$（为了方便，设 $n$ 是 $2$ 的幂，同时用 $c_1$ 代替 $\Theta(1)$，用 $c_2n$ 代替 $\Theta(n)$），得到 $$T(n)= \begin{cases}c_1& \text { if } n=1 \\ 2T(\frac{n}{2}) + c_2n & \text { otherwise }\end{cases}$$

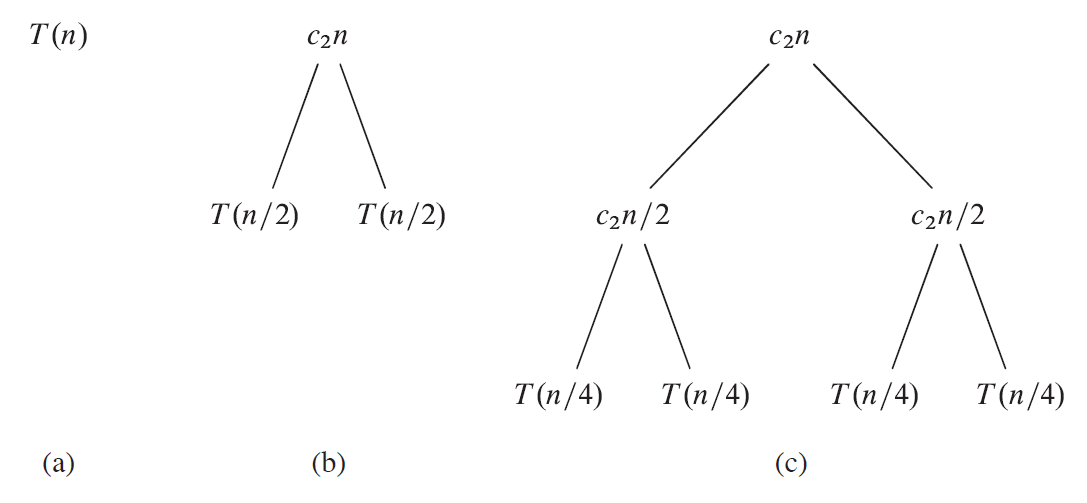
图 (a) 表示原式子
图 (b) 表示进行一次递归，把 $T(n)$ 代换成了 $c_2n$（根节点）加上两个子节点 $2T(\frac{n}{2})$
图 (c) 表示继续再递归一层，把两个 $T(\frac{n}{2})$ 也代换掉了
接下来的图 (d) 表示递归到最深层后，整棵树的样子。

可以看到，除了最底层叶子节点，每一层都是 $c_2n$ 的时间，这样的层数是 $\lg n$ 层。最后一层是 $n$ 个常数问题规模的子问题，所以最后一层需要时间 $c_1n$。因此，总共需要 $c_2n \lg n + c_1n$ 的时间，即 $\Theta(n \lg n)$。

快速排序 Quicksort

归并排序虽然时间复杂度很不错，但是它不是 原址排序（sort in place），也就是说，归并排序的额外空间使用高于常数级别。

快速排序是一种 原址排序，也使用了分治的思想，期望时间复杂度是 $\Theta(n \lg n)$，且常数很小。不过，它在最坏情况下是 $\Theta(n^2)$ 的

快速排序的三个分治步骤是：

分解 divide：选取一个下标 $q$，将数组 $A[p..r]$ 划分为两个（可能为空的）子数组 $A[p..q-1]$ 和 $A[q+1,r]$，使得前一个子数组的每个元素都小于等于 $A[q]$，后一个子数组的所有元素都大于等于 $A[q]$
解决 conquer：递归，对两个子数组进行快速排序
合并 combine：快速排序无需这个步骤，因为快速排序是原址排序的，所以递归结束后两个子数组就已经有序了，进而整个数组都是有序的

由此看来，快速排序最重要的部分是第一步：分解。

快速排序的核心：`PARTITION`

PARTITION 选取当前数组最右端的元素 $A[r]$ 作为主元，以它作为中间点，划分数组。注意，这个划分只是把比主元小的挪到左边去，把比主元大的挪到右边去，并不进行排序。

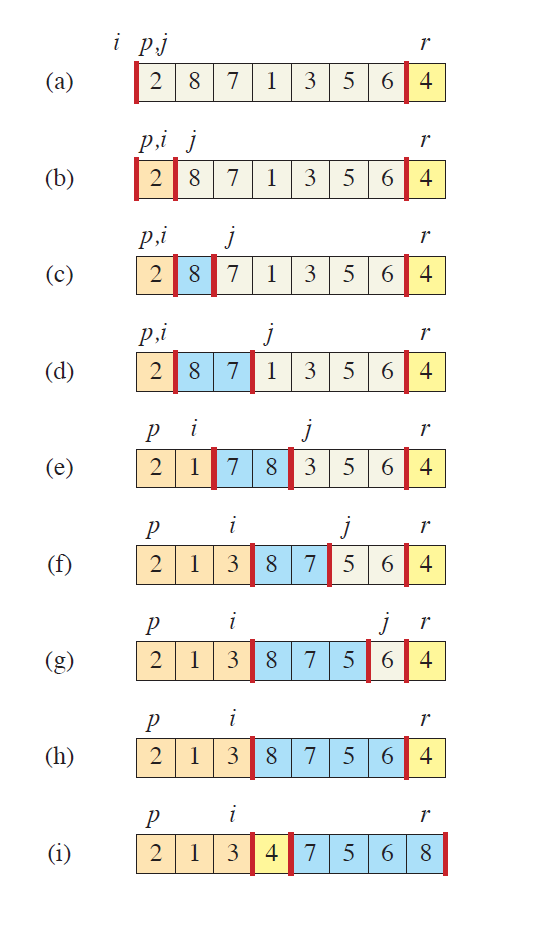
以这张图为例（黄色表示主元，橙色表示（$A[p..i]$）被划分到小于等于主元区域的值，蓝色表示（$A[i+1..j-1]$）被划分到大于主元区域的值，白色表示（$A[j..r-1]$）还未被划分的元素）

图 (a) 表示 PARTITION 循环开始之前的状态。$A[r]$ 被选为主元，用黄色标识。此时 $i$ 初始化为 $p-1$，$j=p$
图 (b) 表示 $2$ 自己与自己交换，即把自己放在了小于等于区域。
图 (c) 和图 (d) 继续进行循环，由于 $8$ 和 $7$ 都比主元大，所以不被交换，分配给蓝色区域，$j$ 持续增长
图 (e) 终于遇到了比主元小的元素，增加一个橙色区域的槽位，把最左边的的蓝色区域元素换到后面去
图 (f) 又遇到一个比主元小的，划分给橙色区域，最左边的蓝色元素被换到右边去
图 (g) 和图 (h) 没找到小于主元的元素，所以都分给蓝色区域，循环结束
图 (i) 是最后一步：退出循环，把主元换到中间，结束

`PARTITION` 过程的循环不变量

上述 PARTITION 过程当中每一次循环开始之前，都满足：

若 $k \in [p, i]$ 则 $A[k] \leq x$，也就是橙色区域
若 $k \in [i+1, j-1]$ 则 $A[k] > x$，对应着蓝色区域
若 $k = r$ 则 $A[k] = x$，即主元的位置始终不变

该不变式没有涉及到 $k \in [j, r-1]$ 的情况，这对应着白色未知区域，没有特殊性质。

下面证明该循环不变量在初始化（initialization）（第一轮循环开始前）阶段和保持（maintenance）（每一轮循环结束）阶段都为真，并且在终止（termination）阶段可以体现算法正确性：

初始阶段，前两条都是空集，显然成立；第三条也显然成立
保持阶段，分两种情况考虑
- $A[j] > x$，此时只有 $j$ 的值发生变化，所以仅考虑第二条性质是否依然成立。显然依旧成立。
- $A[j] \leq x$，此时 $i, j$ 都自增，且发生了交换。分别考虑三条性质：
  1. 因为本来是 $A[j] \leq x$ 的，而 $A[j]$ 被换到了 $i$ 位置，所以此时 $A[i] \leq x$ 成立，故第一条仍然成立
  2. 只需判断 $A[j-1] > x$ 是否成立。其实这个 $A[j-1]$ 就是交换之前的 $A[i]$，也就是上一轮的 $A[i+1]$。由于上一轮 $A[i+1]>x$ 成立，所以这一轮的 $A[i] > x$ 本成立，交换并自增 $j$ 后使得 $A[j-1]>x$ 成立。故第二条仍然成立
  3. $A[r]$ 没有发生变化，所以第三条仍然成立
终止阶段，$j=r$，整个数组被完全划分成了三段：$[p, i]$，$[i+1, j-1]$，$[j=r, r]$，分别是所有小于等于主元的、大于主元的、一个主元。故该算法是正确的。

快速排序性能分析

快速排序的性能依赖于划分是否平衡，而划分是否平衡又依赖于主元的取值。如果划分平衡，那么快速排序的性能与归并排序相同；如果划分不平衡，那么快速排序的性能退化为接近插入排序。

显然，PARTITION 过程的时间复杂度是 $\Theta(n)$ 的。

最坏情况

最坏情况就是，划分产生了一个大小为 $n-1$ 的子数组、一个大小为 $0$ 的子数组、一个主元，且每一轮划分都是如此，即：输入的原数组是已经升序或降序排序好了的。那么此时，$$\begin{aligned}T(n) &= \Theta(n) + T(n-1) + T(0) \\ &= \Theta(n) + T(n-1) + \Theta(1) \\ &= \Theta(n) + T(n-1) \\ &= \Theta(n^2)\end{aligned}$$

最好情况

最好情况下，每次划分，产生的两个子问题规模分别是 $\lfloor \frac{n}{2} \rfloor$ 和 $\lceil \frac{n}{2} \rceil - 1$，此时 $$T(n) = \Theta(n) + 2T(\frac{n}{2}) = \Theta(n \lg n)$$

平衡的情况

假如每次划分，不是 $0 : n-1$，而是 $\frac{n}{10} : \frac{9n}{10}$，那么此时的性能是怎样的？

直观上，感觉这样的划分好像很不平衡，会很慢，但实际上这样划分依然是 $O(n \lg n)$。画出下面这棵树，如图，在前 $\log_{10}n$ 层，每一层的总时间代价都是 $n$；总共有 $\log_{\frac{10}{9}}n$ 层，之后每一层的代价都 $\leq n$，所以总代价依然是 $O(n \lg n)$ 的。

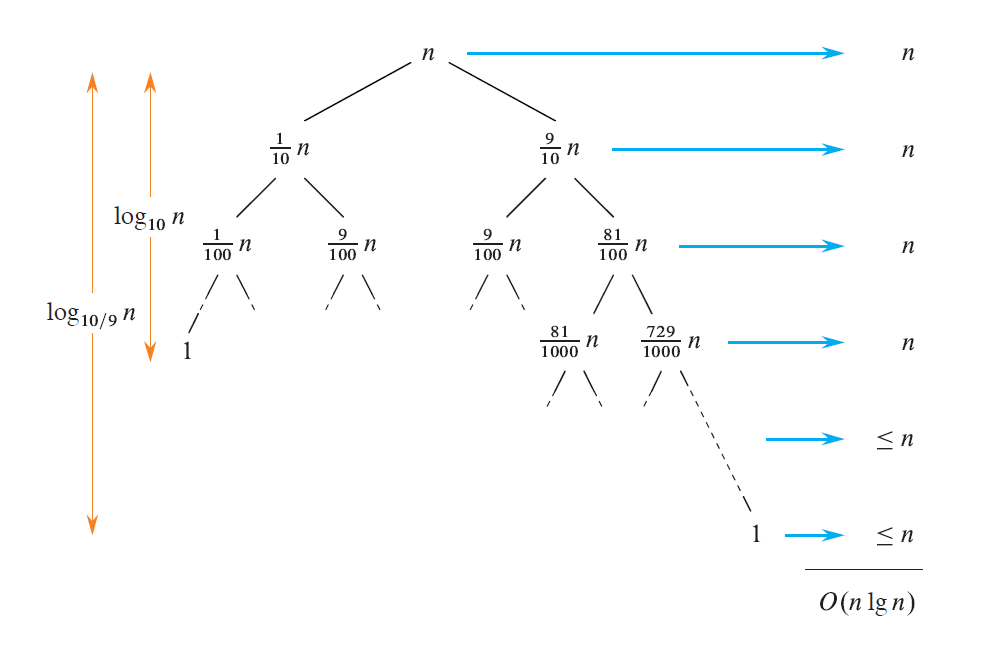
事实上，就算每次划分都是 $\frac{n}{100} : \frac{99n}{100}$ 这样荒唐比例，它也依然是 $O(n \lg n)$ 的——只要不是常数就行。